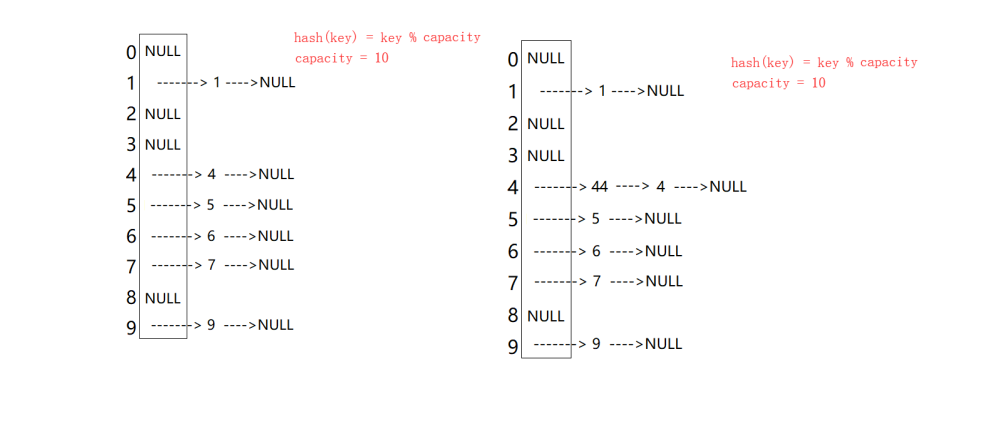
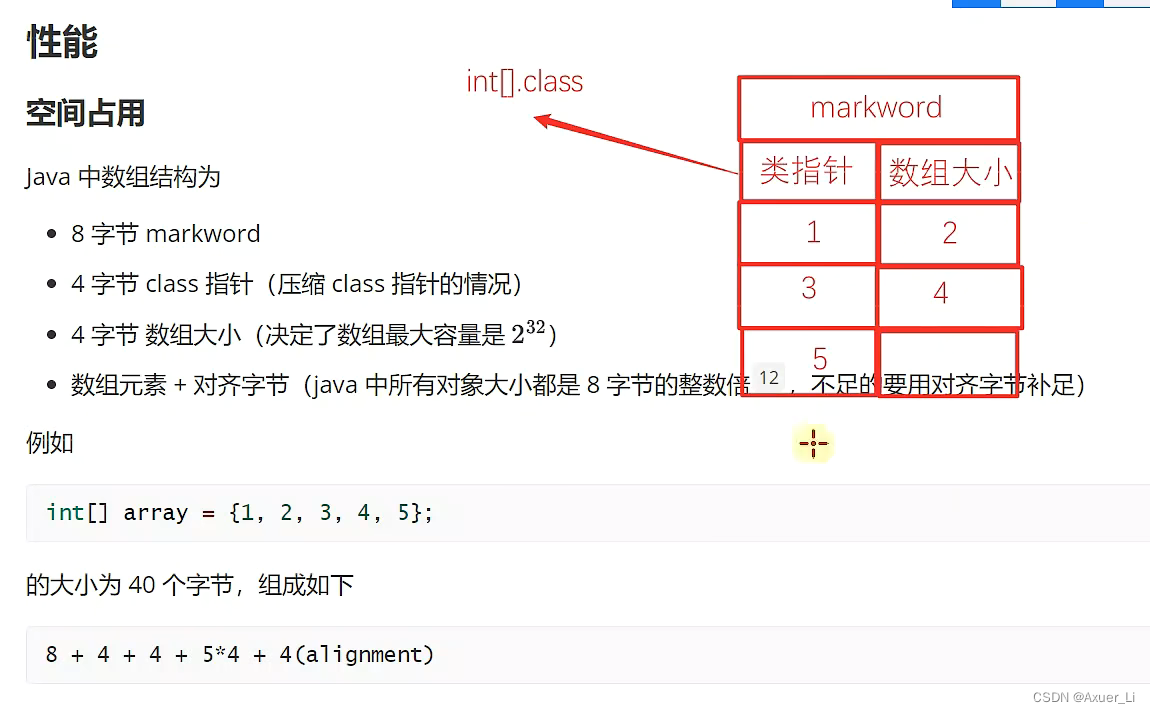
静态数组

在这里插入图片描述

动态数组

把动态数组封装为一个类

1、属性

public class DynamicArray implements Iterable<Integer> {
    private int size = 0; 		// 逻辑大小(有效的元素个数)
    private int capacity = 8; 	// 容量
    private int[] array = {};  	// 动态数组
}

2、方法

1）在末尾添加元素

【方法一】：直接在末尾添加

    /**
     * 向最后位置 [size] 添加元素
     *
     * @param element 待添加元素
     */
    public void addLast(int element) {
        array[size] = element;
        size++;
    }

因为原本数组size就是指向最后一个有效元素的后一个元素

【方法二】：调用后面的add方法，指定索引为size

    /**
     * 向最后位置 [size] 添加元素
     *
     * @param element 待添加元素
     */
    public void addLast(int element) {
        add(size, element);
    }

2）在指定索引位置添加（插入）元素

思路：

插入位置原来的元素及其后面的元素整体后移
元素插入

System.arraycopy(要拷贝的数组, 拷贝原数组的索引, 拷贝目标数组, 
									拷贝到目标数组的索引, 拷贝元素个数);

	/**
     * 向 [0 .. size] 位置添加元素
     *
     * @param index   插入索引位置
     * @param element 待添加元素
     */
    public void add(int index, int element) {
		//容量检查
		checkAndGrow();
		
        //检查index
        if (index >= 0 && index < size) {
            // 向后挪动, 空出待插入位置
            System.arraycopy(array, index,
                    array, index + 1, size - index);
        }
		//直接插入
        array[index] = element;
        size++;
    }

3）移除元素

思路：

记录要删除的元素
要删除的元素后面的元素整体向前移动

    public int remove(int index) { // [0..size)
        int removed = array[index];
        //最后一个元素不进入该条件，而是直接删除
        if (index < size - 1) {
            // 向前挪动
            System.arraycopy(array, index + 1,
                    array, index, size - index - 1);
        }
        size--;
        return removed;
    }

4）扩容

    private void checkAndGrow() {
        // 容量检查
        if (size == 0) { //数组初始化--> 懒汉式
            array = new int[capacity];
        } else if (size == capacity) {
            // 进行扩容, 扩容为原来的1.5倍
            capacity += capacity >> 1;
            int[] newArray = new int[capacity];
            System.arraycopy(array, 0,
                    newArray, 0, size);
            array = newArray;
        }
    }

3、性能

插入或删除性能：（需要复制移动元素）

头部位置，时间复杂度是 $O (n)$

中间位置，时间复杂度是 $O (n)$

尾部位置，时间复杂度是 $O (1)$ （均摊来说）

二维数组

1、内存结构

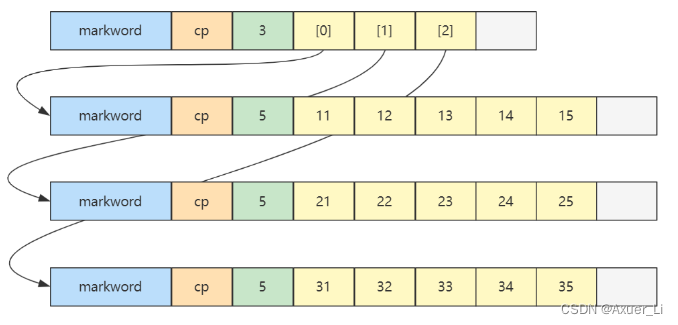
在这里插入图片描述

二维数组占 32 个字节，其中 array[0]，array[1]，array[2] 三个元素分别保存了指向三个一维数组的引用
三个一维数组各占 40 个字节
它们在内层布局上是连续的

2、常用公式

int[][] mat;
int m = mat.length;
int n = mat[0].length;

1）二维数组与一维数组转换

//一维转二维
行索引 = 一维索引 / 列数
列索引 = 一维索引 % 列数
i = x / n
j = x % n

//二维转一维
一维数组索引 = 二维行索引 * 列数 + 列索引
a[x] = a[i*n+j]

假想二维与一维的转换
LC74：搜索二维矩阵

public boolean searchMatrix(int[][] matrix, int target) {
    //变为一维数组(假想)，再二分查找
    int m = matrix.length;
    int n = matrix[0].length;

    int low = 0;
    int high = m * n - 1;

    //当成一维进行二分
    while(low <= high) {
        int mid = (low + high) >>> 1;

        if(target < matrix[mid / n][mid % n]) {
            high = mid - 1;
        } else if(matrix[mid / n][mid % n] < target) {
            low = mid + 1;
        } else {
            return true;
        }
    }
    return false;
}

2）对角线遍历

for(int i = 0,j = m - 1 ; i < m ; i++ , j--) {
	//从左上角往右下角走
    System.out.print("正对角线:" + mat[i][i] + " ");
    //从左下角往右上角走
    System.out.print("副对角线:" + mat[j][i] + " ");
}