目录
引入:
一、神经网络(NN)复杂度
空间复杂度
时间复杂度
二、学习率
三、指数衰减学习率——解决lr的选择
1.总结经验
2.公式引入
四、激活函数
1.简单模型:最初的理解
2.激活函数MP模型
3.优秀的激活函数的特点
4.常见的激活函数
a)Sigmoid()函数
图像
特点
b)Tanh()函数
c)Relu()函数
d)Leaky Relu函数
五、损失函数
1.均方误差
2.自定义
3.交叉熵
4.softmax与交叉熵结合
六、欠拟合与过拟合
1.图像直观引入
2.欠拟合
3.过拟合
4.正则化缓解过拟合
七、优化器
1.常见的优化器
SGD(无momentum),常用的梯度下降法
SGDM(含momentum的SGD),在SGD基础上增加一阶动量
Adagrad,在SGD基础上增加二阶动量
RMSProp,SGD基础上增加二阶动量
Adam, 同时结合SGDM一阶动量和RMSProp二阶动
总结
引入:
前向传播:从输入到输出(执行方向)
反向传播:从输出到输入(优化参数)
训练过程:前向传播->反向传播->前向传播->反向传播 。。。。。->结果(不断优化直到数据用完)
一、神经网络(NN)复杂度
概念:NN复杂度:多用NN层数和NN参数的个数表示,神经网络层有:输入层和隐藏层和输出层,但输入层是不算层的,前一个输出等于后一个的输入

空间复杂度
层数 = 隐藏层的层数 + 1个输出层 左图为2层NN
总参数 = 总w + 总b 左图3x4+4(第1层) + 4x2+2(第2层) = 26
时间复杂度
乘加运算次数 左图 3x4(第1层) + 4x2( 第2层) = 20 时间复杂度
二、学习率
作用:反向传播,根据损失函数的梯度方向,进行更新y=w*x+b中的w参数

总结经验:lr=0.001过慢,lr=0.999不收敛
三、指数衰减学习率——解决lr的选择
1.总结经验
可以先用较大的学习率,快速得到较优解,然后逐步减小学习率,使 模型在训练后期稳定。
2.公式引入
指数衰减学习率 = 初始学习率 * 学习率衰减率( 当前轮数 / 多少轮衰减一次 )
四、激活函数
1.简单模型:最初的理解

2.激活函数MP模型
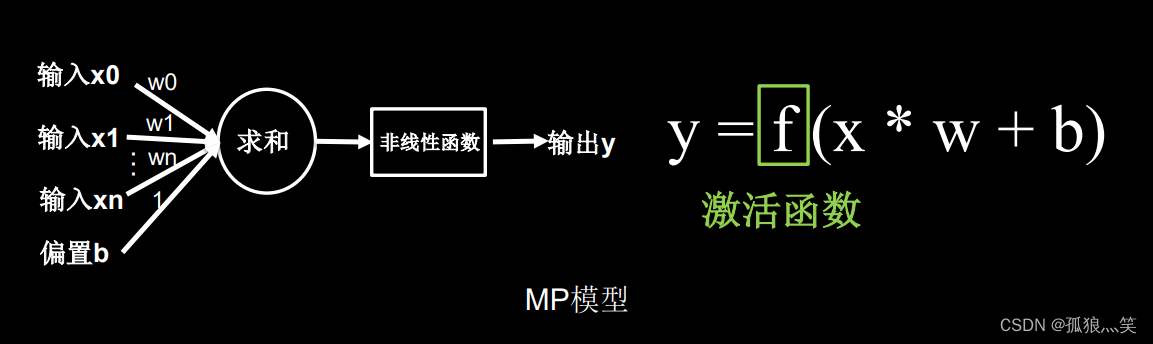
3.优秀的激活函数的特点
- 非线性: 激活函数非线性时,多层神经网络可逼近所有函数
- 可微性: 优化器大多用梯度下降更新参数
- 单调性: 当激活函数是单调的,能保证单层网络的损失函数是凸函数
- 近似恒等性: f(x)≈x当参数初始化为随机小值时,神经网络更稳定
输出有限无限注意点
激活函数输出为有限值时,基于梯度的优化方法更稳定
激活函数输出为无限值时,建议调小学习率
4.常见的激活函数
a)Sigmoid()函数
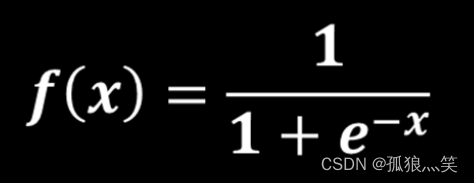
图像
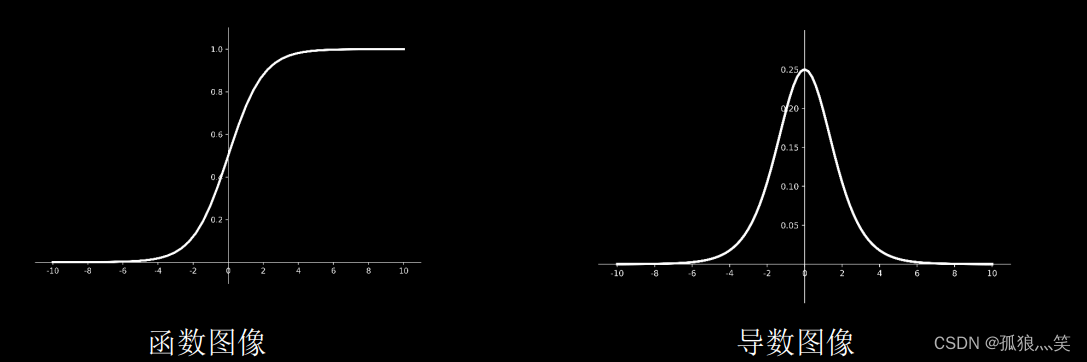
特点
特点 (1)易造成梯度消失 (2)输出非0均值,收敛慢 (3)幂运算复杂,训练时间长
b)Tanh()函数

图像

特点 (1)输出是0均值 (2)易造成梯度消失 (3)幂运算复杂,训练时间长
c)Relu()函数

图像

优点: (1) 解决了梯度消失问题 (在正区间) (2) 只需判断输入是否大于0,计算速度快 (3) 收敛速度远快于sigmoid和tanh
缺点: (1) 输出非0均值,收敛慢 (2) Dead RelU问题:某些神经元可能永远不会 被激活,导致相应的参数永远不能被更新。
d)Leaky Relu函数

图像
理论上来讲,Leaky Relu有Relu的所有优点,外加不会有Dead Relu问题,但是 在实际操作当中,并没有完全证明Leaky Relu总是好于Relu。
激活函数建议
- 首选relu激活函数
- 学习率设置较小值
- 输入特征标准化,即让输入特征满足以0为均值, 1为标准差的正态分布
- 初始参数中心化,即让随机生成的参数满足以0 为均值
五、损失函数
概念:预测值(y)与已知答案(y_)的差距
网络优化:是的loss越来越小,反向传播是的acc更大
- 均方误差:mse (Mean Squared Error)
- 自定义
- 交叉熵损失函数CE (Cross Entropy)
1.均方误差

2.自定义
目的:比如买东西,货多买的少,那成本就高,货少买的多,那么利润就少,但是利润 !=成本

乘一下权重就可以了
3.交叉熵

4.softmax与交叉熵结合
输出先过softmax函数,再计算y与y_的交叉熵损失函数。
六、欠拟合与过拟合
1.图像直观引入
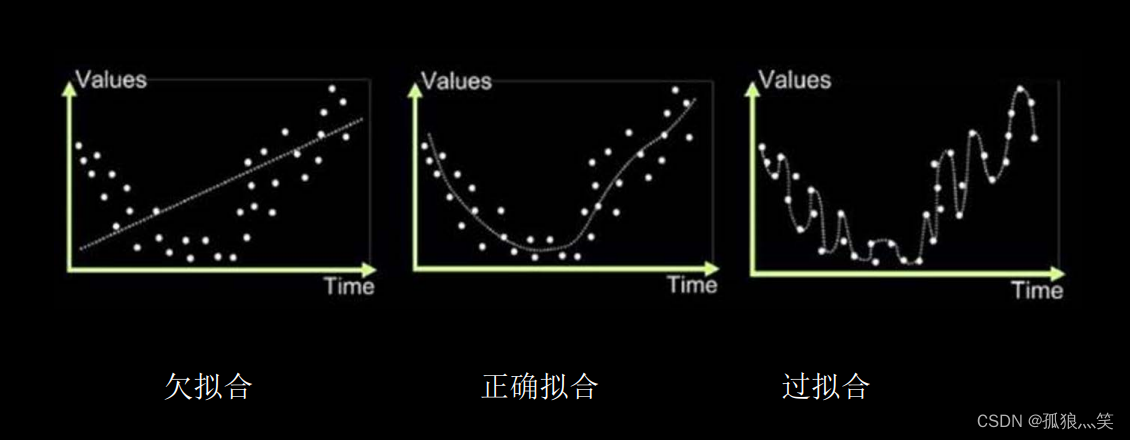
2.欠拟合
欠拟合的解决方法:
- 增加输入特征项
- 增加网络参数
- 减少正则化参数
3.过拟合
过拟合的解决方法:
- 数据清洗
- 增大训练集 采用正则化
- 增大正则化参数
4.正则化缓解过拟合
正则化在损失函数中引入模型复杂度指标,利用给W加权值,弱化了训练 数据的噪声(一般不正则化b)
loss = loss( y与y_ ) + REGULARIZER * loss(w)
正则化的选择
L1正则化大概率会使很多参数变为零,因此该方法可通过稀疏参数 ,即减少参数的数量,降低复杂度。
L2正则化会使参数很接近零但不为零,因此该方法可通过减小参数 值的大小降低复杂度
七、优化器
概念:待优化参数 优化器框架𝒘,损失函数𝒍ose,学习率𝒍r,每次迭代一个batch, t表示当前batch迭代的总次数:
1.常见的优化器
-
SGD(无momentum),常用的梯度下降法
-
SGDM(含momentum的SGD),在SGD基础上增加一阶动量
-
Adagrad,在SGD基础上增加二阶动量
-
RMSProp,SGD基础上增加二阶动量
-
Adam, 同时结合SGDM一阶动量和RMSProp二阶动
备注:这里就不一一解释了,每一个优化器都是在反向传播过程中与损失函数结合来优化参数的,得出更精确的数据,选择精度越高,则内存越大,精度适中,内存始终,自己来决定
作用:优化器就是在深度学习反向传播过程中,指引损失函数(目标函数)的各个参数往正确的方向更新合适的大小,使得更新后的各个参数让损失函数(目标函数)值不断逼近全局最小
总结
- 本文主要借鉴:mooc曹健老师的《人工智能实践:Tensorflow笔记》
- 正向传播:激活函数
- 反向传播:损失函数、优化器
- 欠拟合和过拟合:利用正则化来环节
-
深度学习过程:前向传播,损失函数,优化器,反向传播更新w和b