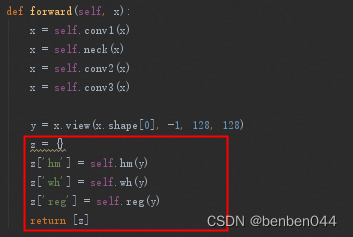
题目

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为root。除了root之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。给定二叉树的root。返回在不触动警报的情况下，小偷能够盗取的最高金额。

示例

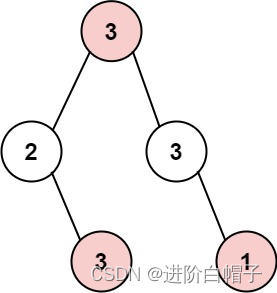
• 输入: root = [3,2,3,null,3,null,1]
• 输出: 7
• 解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7

题解

题目很好理解，小偷也需要会二叉树，不然容易出发报警。题目的意思是其实很简单，就是小偷第不能在父子节点同时打劫。以示例中的例子来进行说明。
第一步是对根节点的判断，根节点有两种选择一种是打劫，一种是不打劫。

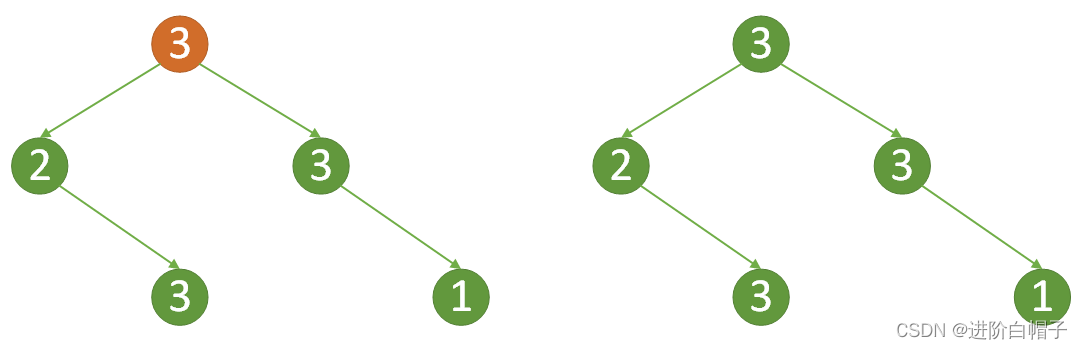
至于是打劫还是不打劫，需要根据后续的子树进行判断。如果根节点选择打劫的话那么根节点的子节点2与3均不能打劫，这种情况下整个树的能打劫的最多金额就从根节点转移到了左右子树。根节点能打劫这种情况的获得最高金额就可以写成：根节点的值3+左子树获得的最高金额+右子树获得的最高金额。这里左右子树的根节点均不可打劫。可见需要分两种情况对子树进行处理。这里明显也是一个递归过程。
这里为了好理解假设f(node)表示针对以node为根节点的子树打劫其根节点的情况下整个子树能获得的最高金额。p(node)表示针对以node为根节点的子树不打劫其根节点的情况下整个子树能获得的最高金额。我们可以写出其递归方程如下：
f(node)=node.value+f(node.left)+f(node.right)
p(node)的情况要稍微复杂一些，因为node没选，所有其左右子树有两种情况，即可选可不选。那么我们如何来判断是两个子树的根节点选还是不选。

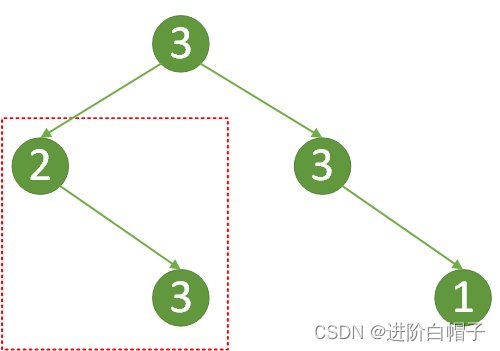
比如上图所示的如何判断[2,3]这刻子树是的根节点2是选还是不选呢。只需要计算[2，3]这根子树两种情况的打劫金额即可，max(f([2,3],p([2,3])))。那么p(node)的递归方程可以写成如下形式：
p(node)=max(f(node.left),p(node.left))+max(f(node.right),p(node.right))
那么接下来我们可以写递归函数了。这里写下我们思路，由于需要区分根节点选与不选，我这里很直接，参数加一个select,select为1的表示打劫根节点。
那么代码写成如下形式：

class Solution:
    def rob(self, root: Optional[TreeNode]) -> int:
        @cache
        def dfs(select,curr_node):
            #终止条件，节点不存在终止
            if not curr_node:
                return 0
            #选择当前子树根节点
            if select==1:
                #f(node)的方程式
                return curr_node.val+dfs(0,curr_node.left)+dfs(0,curr_node.right)
            else:
                #p(node)的方程式
                return max(dfs(0,curr_node.left),dfs(1,curr_node.left))+max(dfs(0,curr_node.right),dfs(1,curr_node.right))
        return max(dfs(1,root),dfs(0,root))

这个代码不加装饰器@cache会超时，显然存在大量的重复计算需要利用记忆化搜索方法提高效率。

这个代码也可以稍微修改成官方代码的形式，即递归函数是一个输入，不需要加select区分，把两种情况的结果均返回。

class Solution:
    def rob(self, root: Optional[TreeNode]) -> int:
        @cache
        def dfs(curr_node):
            #终止条件，节点不存在终止
            if not curr_node:
                return [0,0]#第一个表示选根节点情况，第二个返回提是不选根节点的情况
            left=dfs(curr_node.left)
            right=dfs(curr_node.right)
            #递归方程
            return [curr_node.val+left[1]+right[1],max(left)+max(right)]
        return max(dfs(root))

这两种计算复性上没有区别。

计算复杂度

时间复杂度$O(n)$，因为这里只对整个树的所有节点遍历一次，n表示树中节点个数。
空间复杂度$O(n)$，空间复杂度跟哈希表空间有关，这里递归hash表的空间代价为$O(n)$。