【coarse-to-fine：基于频谱和空间损失约束】

UPanGAN: Unsupervised pansharpening based on the spectral and spatial loss constrained Generative Adversarial Network

（UPanGAN：基于频谱和空间损失约束的生成式对抗网络的无监督全色锐化）

研究发现，在大多数基于神经网络的全色锐化方法中，多光谱（MS）图像被作为真实图像，而下采样全色（Pan）和MS图像被作为训练数据。然而，从降采样图像训练的模型不适合于具有丰富空间和光谱信息的MS图像在其原始空间分辨率下的全色锐化。针对这一问题，本文提出了一种基于谱和纹理损失约束的生成式对抗网络（GAN）的迭代网络进行全色锐化。首先，GAN不是直接输出融合图像，而是集中于生成平均差图像（mean difference image）。GAN的输入是一个良好的初始差分图像（initial difference image），这将使网络更好地工作。其次，设计了由coarse-to-fine的融合框架，生成融合影像。该方法利用两个优化的鉴别器对生成的图像进行鉴别，并对PAN和MS图像进行多级融合处理，生成全分辨率下最佳的全色锐化图像。最后，将设计好的损失函数嵌入到生成器和鉴别器中，以精确地保持融合图像的保真度。

介绍

迄今为止，已经发射了许多光学对地观测卫星，如QuickBird、GeoEye-1、GaoFen-2和WorldView-3，以同时获取全色（Pan）和多光谱（MS）图像。由于Pan和MS传感器必须在空间分辨率和光谱分辨率之间进行基本权衡，因此MS图像的空间分辨率低于Pan图像的空间分辨率。然而，在地图更新和城市调查等许多应用中，具有与Pan图像相同空间分辨率的MS图像更受欢迎。因此，全色锐化（PS）技术已经被开发出来，通过将来自Pan图像的高空间细节注入到MS图像中来在空间上增强MS图像。
现有的全色锐化方法可以分为五类：（1）构件代换（CS）方法;（2）多分辨率分析（MRA）方法;（3）变分优化（VO）方法;（4）无生成对抗网络（GAN）的深度学习方法;（5）基于GAN的深度学习方法。随着深度学习技术的发展，几种网络框架被用于全色化。从网络结构的角度，将基于深度学习的方法分为无GAN-free和基于GAN-based两类。

The CS methods

CS方法通过矩阵变换将MS图像的像素值投影到一个新的特征空间，然后用全景图像全部或部分替代MS图像的第一个投影分量，最后将这些分量进行逆投影以锐化MS图像。强度-色调-饱和度（IHS）、主成分分析（PCA）、Brovey变换（BT）和Gram-Schmidt变换（GS）都属于这一类。
2004年，提出了一种新的快速IHS方法（FIHS）。这个方法除具有计算速度快的特点外，还将传统的三阶变换推广到任意阶的变换。但FIHS算法也存在IHS算法同样的问题，即会引起频谱失真。自适应IHS（AIHS）通过对全色图像和多光谱图像线性组合的误差进行近似来计算不同通道的融合比。改善AIHS (IAIHS)使用多光谱图像的梯度信息来分配不同的权重系数不同的渠道,以便不同的细节可以注入每个通道。PCA是一种统计方法,可以将多变量数据与相关变量转换为不相关的变量。PCA算法的优点是适合多波段图像融合。融合后的图像空间分辨率高，细节信息好，受噪声影响小。但缺点是频谱失真严重。

BT 融合方法是使用颜色标准化变换对MS图像进行变换，然后将MS图像的三个波段与高分辨率Pan图像进行乘积。BT的优点是很好地保持了整体结构信息，但会有光谱失真。GS 融合方法不仅能很好地保留全景图像的空间细节，而且速度快。IHS、PCA、BT和GS等全色锐化技术对空间细节信息的保真度较高，且具有速度快、易于实现等优点。然而，这些方法仍然具有局限性。当高分辨率全色图像和低分辨率多光谱图像之间存在强相关性时，它们工作得很好。然而，它们无法解释全色和多光谱图像之间光谱失配引起的局部差异。因此，融合图像会产生明显的光谱畸变。

The MRA methods

多分辨率分析（MRA）算法是对源图像进行变换得到表达系数，再对表达系数进行逆变换得到最终的图像融合结果。基于MRA的方法大多采用小波变换和曲线变换。用于提取空间细节的常用模型包括：小波、离散小波、加性小波亮度比例（AWLP）、引导滤波器、曲波、Contourlet和拉普拉斯金字塔等。小波变换具有良好的时频局部分析特性，能够表征图像在水平、垂直和对角线方向上的特征信息。Ranchin T等人于1993年首先提出了一种基于离散小波变换的图像融合算法，并取得了良好的融合效果。然而，由于小波变换图像的大小不同，配准精度会影响融合图像的质量。比较了Curvelet和Contourlet等多种多分辨率分解算法，研究了分解层数和滤波器选择对融合性能的影响。有学者提出了一种基于离散小波包变换的多传感器图像融合算法。该方法能够充分融合源图像中的信息，提高图像的信息分析和特征提取能力。Burt P.J 提出了一种基于拉普拉斯金字塔变换的图像融合算法。金字塔变换融合算法能够在不同尺度上表现图像的重要特征和细节。

The VO methods

最早的变分融合方法是C.Ballester提出的P+XS。其基本思想是从全色影像中提取空间信息，并将其叠加到MS影像中，以提高MS影像的空间分辨率。M. Möller提出了变分小波全色锐化算法。他们在小波融合图像中引入匹配项，并结合P+XS模型的几何匹配增强纹理。在小波域中执行最小化允许不同的参数被用于不同级别的小波分解。此外，增加了两个函数项，以帮助提高空间信息的质量，并保持不同波段之间的关系。Chen等人提出了基于局部谱一致性和动态梯度稀疏融合的动态梯度稀疏融合（DGSF）。变分法能较好地保护光谱信息和空间信息。此外，VO方法在空间保真度和频谱保真度之间实现良好的平衡仍然是一个挑战。Deng等人基于可再生核Hilbert空间和Heaviside函数提出了一种很好全色锐化方法。然后，Tian等人提出了一种创新的解决方案，使用Cartoon-texture Similarities（卡通纹理相似性），该方案可以很好地保留全局和局部空间细节，并获得高质量的全色锐化图像。但能量泛函的求解过程过于复杂，算法的时间复杂度很高，难以具有实时性。

The GAN-free deep learning methods

随着深度学习技术的发展，出现了卷积神经网络、深度残差网络、递归神经网络、自动编码器等几种公认的深度学习框架，这些网络被引入到全色锐化领域并取得了显著的效果。基于深度学习的全色锐化方法首先受到超分辨率方法的启发。MS影像全色锐化可以看作是一种特殊的超分辨率技术，利用同时采集的Pan图像实现MS图像的超分辨率。从这个观点出发，通过修改基于卷积神经网络（CNN）的超分辨率方法来设计新颖的全色锐化神经网络（PNN）以执行全色锐化工作。近年来，注意机制被用于调节光谱保真度和空间保真度。例如，有学者设计了信道注意力模型，以自适应地校正信道的特性;为了充分利用MS影像与Pan影像之间固有的相似信息，提出了一种非局部注意残差网络。建立了编码关注度模型和融合关注度模型来提高融合图像的轮廓信息。

此外，还将几种混合策略引入到全色锐化领域。2017年，有学者提出了一种称为PanNet的混合模型方法。它们在高通滤波域中训练网络以保持空间结构，并且为了光谱保持，它们将上采样MS图像添加到网络输出。随后，T. Benzenati等人提出了一种两阶段全色锐化网络，其中，在第一阶段，CNN包括广义拉普拉斯金字塔来预测初始空间信息。将分量替换和多分辨率分析融合方法引入到神经网络中来估计非线性信息注入模型。设计了一种新颖的映射CNN，将Pan影像与MS影像之间的差异信息映射为Pan影像与融合影像之间的差异信息。提出了一种分组多尺度膨胀卷积深度细节网络结构，用于多波段光谱信息的全色锐化。此外，一种新的方法将流行的Transformer架构引入到全色锐化领域，其目的是建立长距离依赖性，以充分利用更多有用的特征。这些方法可以产生具有竞争力的性能。然而，它们也受到缺乏理想融合图像的限制，并且依赖于降采样的Pan和MS图像作为训练样本。

The GAN-based deep learning methods

GAN 是一种重要的机器学习架构，其中生成器和鉴别器相互竞争，以逐渐获得更准确的预测。2020年，首先构建了一个全色锐化GAN（PSGAN）来融合Pan和MS图像融合。PSGAN在降采样Pan和MS图像上实现了高保真度全色锐化结果。随后，将残差网络编码器-解码器模型引入到生成器中，并构造了条件鉴别器网络以保留更多的空间信息。最近，将MS影像的全色锐化转换为全色影像的彩色化，并据此提出了全色化GAN框架（PCGAN）。此外，为了提高全分辨率场景下的融合性能，提出了一种基于GAN的全色锐化模型，该模型可以通过全分辨率Pan和MS图像进行训练;最近，还设计了一个具有全分辨率光谱和空间鉴别器的全色锐化GAN。这两种模型在避免缺乏理想训练样本方面都取得了突破。在2022年，构建了一个基于梯度和强度的双重鉴别器的GAN网络，以有效地对图像进行全色锐化。该算法能保证生成的图像包含期望的几何结构和显著信息，达到最佳的全色锐化效果。然而，这些模型在处理具有丰富空间和光谱信息的图像时，往往仍会遇到失真问题。

由于MS影像的空间信息与Pan影像的空间信息有很大的差异，因此一次向MS影像中注入空间信息也会造成空间畸变。这些方法大大提高了融合性能的空间保真度。这些方法大大提高了融合性能的空间保真度。然而，由于缺乏理想的融合图像，几种方法都是从降采样后的Pan和MS图像中训练出来的。当以MS图像的原始空间分辨率对MS图像进行全色锐化时，这种训练的模型经常导致空间失真，尤其是对于具有尖锐边缘或丰富纹理的区域。本文提出了一种基于频谱和空间损失约束的GAN的无监督全色锐化方法UPanGAN。本文的主要目的如下：
(1)开发一个无监督的全色锐化模型，该模型不需要理想的训练样本。
(2）提高了对具有丰富空间和光谱信息的全分辨率影像的融合性能。

贡献

1）针对训练样本问题，提出了一种直接利用原始Pan和MS影像训练的无监督全色锐化GAN模型。与基于降采样图像训练的模型相比，该模型更适合于具有丰富空间和光谱信息的原始全分辨率图像的全色锐化。
2）设计了一种由coarse-to-fine的融合方案，该方案具有较好的初始差分图像，提高了融合的保真度。如果初始输入较好，网络将工作得更好。由粗到精的融合方案比一步融合方案能更准确地提取均值差图像，得到更好的融合图像。
3）根据空间和光谱保持的要求，采用精心设计的损失函数对UPanGAN训练进行微调。实验表明，该方法确实能获得较好的融合性能。

方法

所提出的模型，UPanGAN由均值差图像初始化模块和一个—>光谱和空间损失约束GAN模块组成。GAN模块包括均值差图像生成器和两个损失约束鉴别器。如图1中所示，
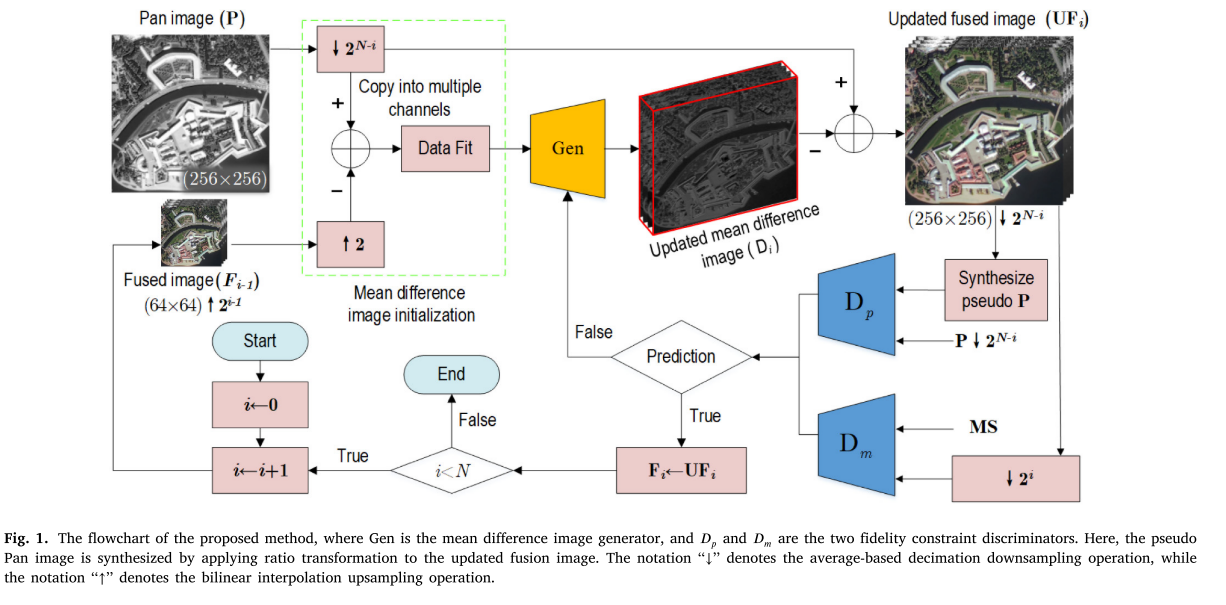
请添加图片描述
UPanGAN是一种从coarse-to-fine融合方案。与一步融合方法相比，由coarse-to-fine的融合方法能够更准确地提取全色影像与MS影像的平均差值图像，从而对空间信息丰富的全分辨率影像进行更好的空间和光谱保持。

假设Pan图像和MS图像之间的空间分辨率比为 $2^𝑁$ 。为了便于讨论，在表1中列出了在以下描述中使用的一些缩写。在这里插入图片描述
该方法首先𝐃_𝟏通过𝐏↓ $2^{𝑁 −1}$ 和𝐅₀ ↑ 2生成均值差图像，然后迭代生成均值差图像，𝐃_𝑖直到𝑖≥𝑁。这里，符号“↓ "表示下采样操作，而符号”↑"表示上采样操作。在该方法中，所有的下采样操作都是通过基于平均值的抽取进行的，而上采样操作是通过双线性插值进行的。这两种方法都是常用的采样方法，且实现简单，效果较好。值得注意的是，如图1所示，我们方法的生成器并不直接生成融合图像𝐅_𝑖，而是通过𝐏↓ $2^{𝑁−1}$ 减去𝐃_𝑖间接获得融合图像，如下所示：
在这里插入图片描述

Mean difference image initialization（均值差图像初始化）

均值差图像初始化受我们之前的CS全色锐化方法的启发。平均差图像是PAN图像和MS图像的平均信息之间的差图像。差异信息越少，融合图像的保真度越好。事实上，如果减少GAN的初始输入和可接受输出之间的差异，GAN可以工作得更好。我们观察到理想融合影像与MS影像之间存在着很大的空间差异，同时理想融合影像与Pan影像之间也存在着很大的光谱差异。然而，在初始平均差图像和可接受的平均差图像之间存在小的变化。因此，与以往基于遗传算法的融合方法不同，该模型通过计算全色影像与融合影像的平均差值图像，而不是直接得到融合影像。
为了初始化合格的平均差图像，采用数据拟合方案来平滑𝐅_𝑖−1 ↑ 2和𝐏↓ $2^{𝑁 −𝑖}$ 之间的差图像。它可以写成
在这里插入图片描述
其中𝐃_𝑖是初始平均差图像，𝐆是高斯滤波器，𝑏是波段序列值。根据我们早期的工作，高斯滤波器的最佳标准差设置为2，其最佳核大小设置为7。经验证，它们是最佳的参数。

Spectral and spatial loss constrained GAN

该对抗式学习结构由三个模块组成，平均差图像生成器、空间鉴别器和光谱鉴别器。如图1所示，所有这些模块都是基于CNN实现的。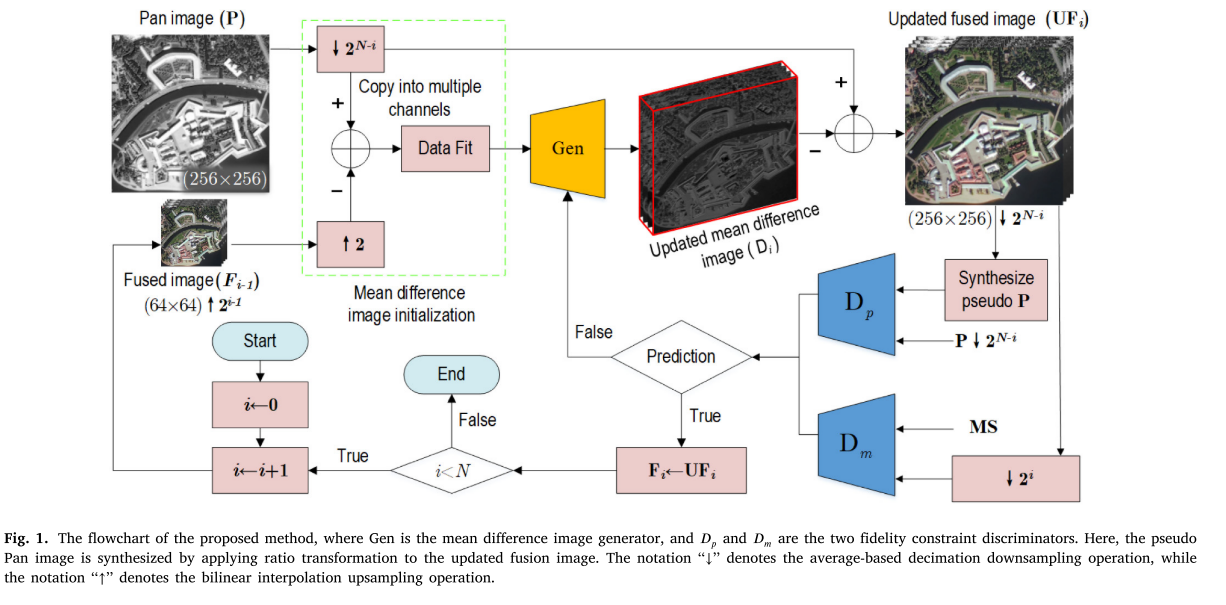请添加图片描述
平均差图像生成器根据精心设计的损耗约束迭代地执行平均差图像（𝐃_𝑖）的微调。光谱和空间鉴别器检查更新的平均差图像是否满足空间和光谱保持约束。

The mean difference image generator

在这里插入图片描述

Network architecture.
图2（a）给出了平均差图像发生器的网络结构。该发生器的优化目标是间接产生足以欺骗空间鉴别器和光谱鉴别器的融合图像。平均差图像生成器具有7个卷积层。在该发生器中，奇数层执行标准卷积运算，而偶数层执行可变形卷积运算。与标准卷积只能提取矩形特征（N × N）不同，可变形卷积可以自适应地捕获任意形状的特征。因此，可变形卷积的添加使得模型生成器能够更好地生成平均差图像。此外，小的卷积核适合于提取初始和可接受的平均差图像之间的微小空间差。因此，对于所有层，卷积核大小被设置为3 × 3;从第一层到第七层，选择Leaky ReLU作为激活函数。然而，对于最后一层，Tanh被视为激活函数。此外，为提高特征图的重用率，均值差图像生成器采用了ResNet开发的跳跃连接。因此，层的输入是其先前层的输入和输出的总和。

所提出的生成器的最终目标是在理想融合图像（𝐅_𝑖）和下采样全景图像（𝐏↓ $2^{𝑁 −𝑖}$ ）之间获得可接受的平均差图像（𝐃_𝑖）。事实上,与融合图像相比,平均差图像与空间细节更穷。我们发现,低层网络能够微调平均差图像。融合之间做一个平衡性能和计算成本,该发生器被设计为一个七层网络。

Loss function
在该发生器中，损失函数（𝑙_𝑔）在生成高保真融合图像中起着关键作用，直接影响融合图像的质量。它由光谱损失函数（ $𝑙^𝑔$ _𝑚）和空间损失函数（ $𝑙^𝑔$ _𝑝）组成。因此，它被定义为𝑙_𝑔= $𝑙^𝑔$ _𝑚+ $𝑙^𝑔$ _𝑝。 $𝑙^𝑔$ _𝑚表示更新的融合图像（𝐔𝐅_𝑖）和之间的差异𝐌𝐒。此处，𝐔𝐅_𝑖计算公式为在这里插入图片描述
然后，频谱损失函数 $𝑙^𝑔$ _𝑚可以写为：
请添加图片描述
其中，𝐾为训练样本总数，𝐵为影像总波段数𝐌𝐒， $𝐌^𝑘$ _𝑏为 $𝐌𝐒^𝑘$ （𝑏）的均值， $^2$ _𝐹为矩阵Frobenius范数。𝛼 是用于调整两个项的权重的设定参数。𝑙_𝑎1是光谱对抗损失，并且用于测量更新的融合图像和原始MS图像之间的光谱信息多样性，其可以定义如下：
请添加图片描述
其中D_𝑚表示光谱鉴别器并且𝑢表示光谱鉴别器对由生成器生成的融合图像的置信度。在设计谱损失函数时，我们考虑了 $𝐌𝐒^𝑘$ （𝑏）的相对值。这样考虑的原因是，当 $𝐌𝐒^𝑘$ （𝑏）的值较小时， $𝐔𝐅^𝑘$ _𝑖（𝑏）的微小变化可能引起明显的频谱失真。提出的光谱损失函数可以放大微弱的光谱变化，避免光谱失真。

由于缺乏理想的融合影像作为参考影像，很难直接度量空间损失。为了解决这一问题，将下采样的全景图像𝐏↓ $2^{𝑁 −𝑖}$ 作为空间参考，然后合成伪全景图像𝐏_𝑖来评估空间损失。为了克服过饱和失真问题，应用比率变换由候选融合图像合成伪全景图像。首先，图像比率𝐑_𝑖计算如下：
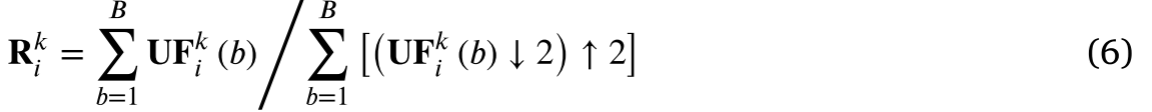
请添加图片描述

其中𝑘是训练样本的序列，𝑏是波段序列值，𝐔𝐅_𝑖是更新的融合图像。然后，伪全景图像定义为请添加图片描述
在这种情况下，空间损耗可以通过𝐏↓ $2^{𝑁 −𝑖}$ 和 $𝐏∧^𝑘$ _𝑖之间的差来精确测量。因此，空间损耗函数最终定义为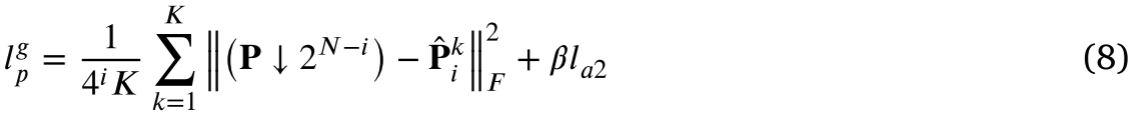在这里插入图片描述
其中，𝛽是用于在第一项和第二项之间取得平衡的设定参数。值得一提的是 $𝑙^𝑔$ _𝑚，和 $𝑙^𝑔$ _𝑝对融合性能同样重要。因此，不会设定其他参数来调整 $𝑙^𝑔$ _𝑚，和 $𝑙^𝑔$ _𝑝的权重。与上述频谱损失类似，我们还在第二项中添加空间对抗损失，如下所示：
请添加图片描述

其中D_𝑝表示光谱鉴别器，并且𝑣表示空间鉴别器对由生成器生成的融合图像的置信度。

The spatial and spectral discriminators

Network architecture
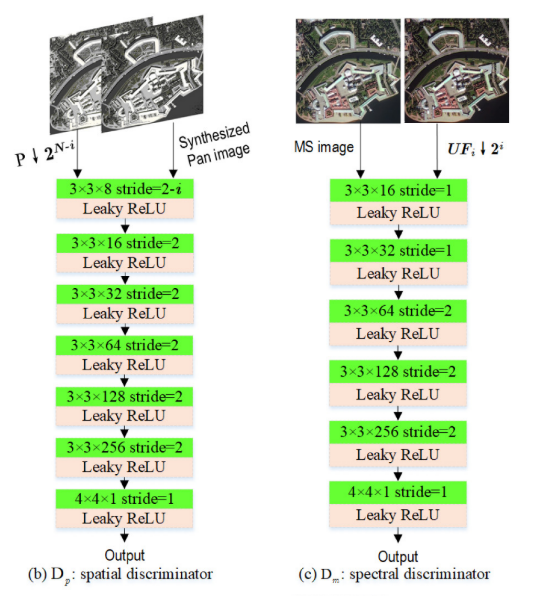
在这里插入图片描述

如图2（b）和（c）所示，空间鉴别器的网络结构与光谱鉴别器的网络结构相似。两个网络的相同组件如下：（1）该𝐷_𝑝结构具有7个卷积层，而𝐷_𝑚具有6个卷积层;(2)前几层的核大小为3 × 3，最后一层的核大小为4 × 4;（3）对于所有卷积层，其提取的特征图的数目被设置为[8/none，16，32，64，128，256，1];（4）将Leaky ReLU作为激活函数。由于空间鉴频器的输入图像尺寸是光谱鉴频器的4倍，因此空间鉴频器的步长与光谱鉴频器的步长不同。因此，空间鉴别器的步长被设置为[2-𝑖，2，2，2，2，2，1]，而光谱鉴别器的步长被设置为[1，1，2，2，2，1]。两个鉴别器分别根据以下损失函数检查更新的融合图像的空间和光谱保真度。最终，当通过保真度检查时，发生器可以提供合格的融合图像。
Loss function
设计了空间损失函数（ $𝑙^𝑑$ _𝑝）和光谱损失函数（ $𝑙^𝑑$ _𝑚），分别用于评价更新融合图像的空间保真度和光谱保真度。评估是一个概率，其值的范围从0到1。为了评估更新的融合图像的空间保真度，类似于发生器的损失函数 $𝑙^𝑔$ _𝑝，根据以下公式通过比率变换合成伪全景图像：请添加图片描述
同样地，在空间鉴别器中，空间损失函数也是通过评估𝐏↓ $2^{𝑁 −𝑖}$ 和 $𝐏∧^𝑘$ _𝑖之间的差异来计算的。这里，𝐏↓ $2^{𝑁 −𝑖}$ 被视为空间目标图像。因此，空间损耗函数定义如下

其中𝑎和𝑏分别表示合成全景图像（ $𝐏∧^𝑘$ _𝑖）和目标图像（ $𝐏^𝑘$ ↓ $2^{𝑁 −𝑖}$ ）的标签;D_𝑝（ $𝐏∧^𝑘$ _𝑖）和D_𝑝（ $𝐏^𝑘$ ↓ $2^{𝑁 −𝑖}$ ）表示伪全景图像和目标图像的分类结果。为了尽可能地区分作为伪图像的融合图像和作为真实的图像的全景图像，在实验中𝑎将设为0，并𝑏将设为1。

在光谱鉴别器中，选择MS图像作为光谱目标图像。类似地，频谱损失函数被写为如下：在这里插入图片描述
其中𝑐和𝑑分别表示下采样融合图像的标签（ $𝐔𝐅^𝑘$ _𝑖↓ $2^𝑖$ ）和目标图像（ $𝐌𝐒^𝑘$ ）,D_𝑚（ $𝐔𝐅^𝑘$ _𝑖↓ $2^𝑖$ ）和D_𝑚（ $𝐌𝐒^𝑘$ ）是下采样融合图像和目标图像的分类结果。这里，𝑐和𝑑在实验中也分别设置为0和1。