1. 摘要
本文提出一个开销较小且鲁棒的激光惯性里程计框架。使用迭代扩展卡尔曼滤波器来实现激光雷达特征点和IMU的紧耦合,可以在快速运动、有噪声或重复纹理等退化环境中鲁棒地定位。为了在测量数据量很大的情况下降低开销,提出了计算卡尔曼增益的新公式。该公式的计算开销依赖于状态量的维度而非测量量的维度。该方法已经在室内和室外环境中进行了测试,在所以有测试中该方法均能可靠运行。
2. 代码地址
GitHub - hku-mars/FAST_LIO: A computationally efficient and robust LiDAR-inertial odometry (LIO) package
3. 引言
固态激光雷达拥有巨大的潜力,但也带来了一些新的挑战:
- 激光雷达的特征点通常是环境中的几何结构(边或平面)。当无人机运行在重复纹理的环境中时,因为没有足够强的特征,所以容易产生退化。当激光雷达的FOV较小时这一问题更加明显。
- 由于沿着扫描方向的高分辨率,每次激光雷达扫描通常包含许多特征(数千)。因为在退化场景这些特征点并不足以可靠地得到位姿,那么把这些特征点与IMU进行紧耦合将会产生巨大的计算开销,对于无人机的是不可接受的。
- 由于激光采样是循序地发射并接收激光,所以同一次扫描过程中的采样点的时间戳各不相同,这会造成畸变,进而影响匹配结果。
论文主要贡献:
- 为了就对快速运动、噪声、重复纹理造成的退化,采用紧耦合迭代卡尔曼滤波器来融合激光雷达特征点和IMU数据。提出了一个规范的反向传播过程去计算运动畸变。
- 为了降低由于数据量大而造成的计算开销大的问题,提出了一个新的公式来计算卡尔曼增益,且证明了它与传统卡尔曼计算公式的等效性。新公式的计算复杂度与状态量的维度相关而非测量量的维度。
- 在一个快速且鲁棒的激光惯性里程计软件包中实现了所有的公式。该系统可以在板上计算平台中运行。
- 使用无人机在不同的室内室外环境中测试了该系统,并验证了在快速运动或者强烈震动的噪声环境下的鲁棒性。
4. 论文架构
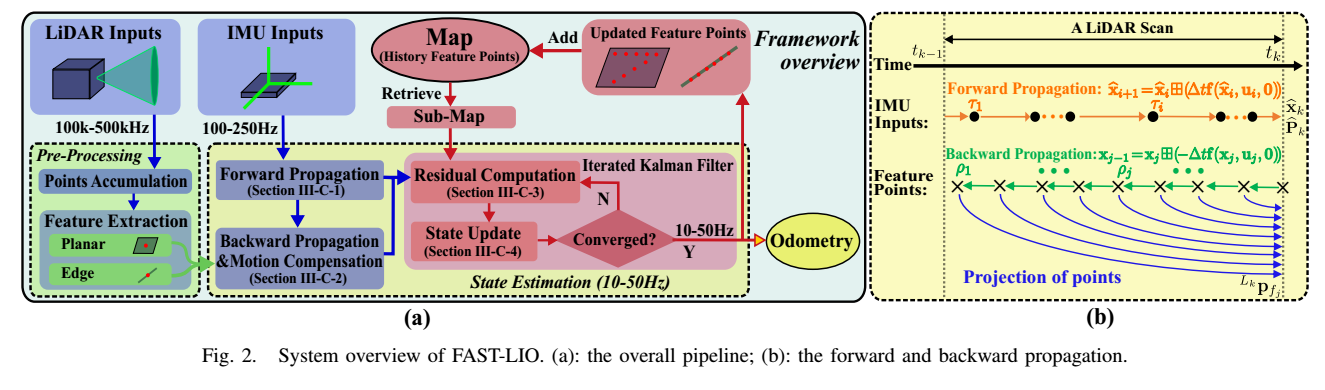
论文架构图如上:输入为激光雷达数据和imu数据。雷达数据经过预处理环节:激光点累积,以及特征提取(平面特征,边缘特征),imu数据经过前向推算,后向推算,以及为激光雷达点云提供畸变去除,在更新过程中,联合IMU和雷达数据构建观测方程,滤波框架采用IEKF。IMU的后向过程是一个后向的推算,主要作用是为雷达去畸变提供运动约束。
5.系统介绍
5.1. 符号定义
定义了两种符号,如下所示,可以支持在旋转矩阵以及流形两种符号的公式表述。当是旋转矩阵时,就代表加减。

5.2. 连续域模型
假设IMU和激光雷达刚性连接,所以它们之间的安装角和杆臂是固定的。如下是连续域下的运动方程,为微分形式。这里把零偏建模成随机游走过程。
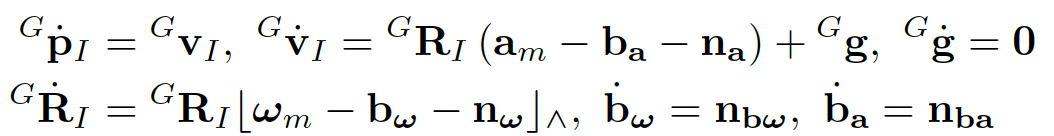
5.3. 离散域模型
离散域下的模型如下所示,连续域转到离散域要乘以采样时间t。

从下面公式可以到,状态变量为18维,这里不太清楚为啥把世界坐标系下的重力放在状态变量中了,因为它本身就是个固定值。

5.4. 雷达数据预处理
雷达原始数据频率非常高,200KHz,在这么高的频率下,不可能做到实时接收,我理解在激光雷达的内部信号处理中,一般做法是累积一段时间,再一块接收,也就是一帧数据,实现降频,在FAST-LIO中,一般为50Hz,按照这个频率计算的话,一帧数据包括4K的原始数据。在论文中,累积处理的时间被记为tk,对于原始数据,我们可以通过高平滑性得到平面特征,低平滑性得到边特征。假设在20ms时间内雷达发生了转弯和线性运动,所以这一帧中的雷达点采集的时间戳是不一样的,每个时间戳对应的位姿也是不一样的,就需要借助IMU来去除运动畸变。
6.状态估计
这是论文的核心内容。
6.1. 前向过程
前向过程其实就是卡尔曼滤波的预测过程,有两个方程:状态变量的预测方程,以及协方差矩阵的预测方程。
如下是系统预测方程。
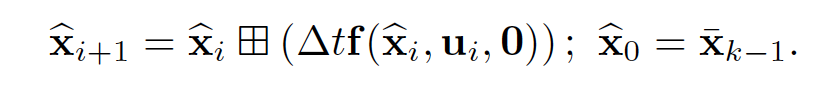
如下分别为系统转换矩阵和噪声转换矩阵。

下面是协方差先验过程。
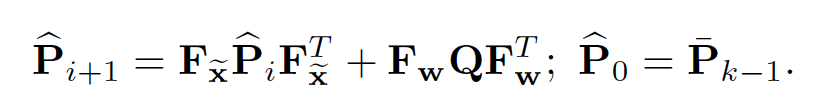
6.2. 后向过程&运动补偿
为何要进行后向过程,其实涉及到一个时间软同步的问题。IMU和激光雷达的时间不可能完全对比,相差在几个ms。激光雷达一帧数据由很多点组成,这些点显然不是同一时间测量得到的,所以需要补偿时间差带来的运动误差。如下所示,已知j刻度的激光雷达点坐标,如何求k时刻的激光雷达点坐标,k时刻代表真正的采集时间,当然,这个时间可以用线性插值方法获取,也存在一定的插值误差,但是一般误差足够小了。需要先转换到IMU坐标系,再通过后方推算得到k时刻IMU坐标下的激光点坐标,最后再转换回到激光雷达坐标系,就得到了k时刻的雷达点坐标系。
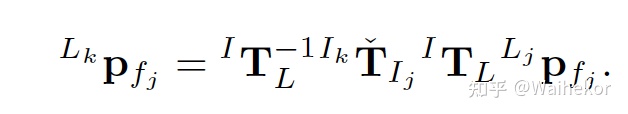
6.3. 残差计算
在补偿完激光雷达的运动畸变之后,我们就得到了用在时间戳tk接收到的所有激光雷达点,构建观测残差信息。
残差计算是为了构建滤波器的观测方程。如下所示,雷达点坐标,先转到IMU坐标系,再转到世界坐标系下。
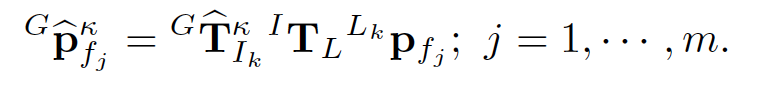
对于每一个激光雷达点,最邻近平面或者边缘被定义为激光雷达点投影到地图上之后的最接近的平面或者边缘。残差就是投影到地图之后的两者之间的距离。观测模型如下图所示:

观测模型中,需要计算地图中最邻近的平面,为了得到这个平面方程,需要用到平面上一点(也就是对应的雷达点投影到地图上的相应点),以及该平面的法向量,所以观测模型如下公式所示:
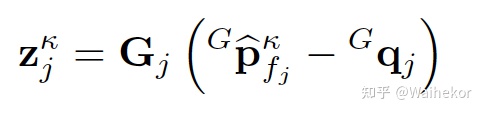
完整的观测方程如下所示,下公式中的u即为法向量,q是图中的平面中对应点。从观测方程中可以看到,IMU欧拉角,IMU和雷达之间的外参也是公式中,可以依靠观测方程被估计出来,我理解这两个待估计量存在耦合性,在标定出其中一个参数的基础上,去估计另外一个参数可能更合适。
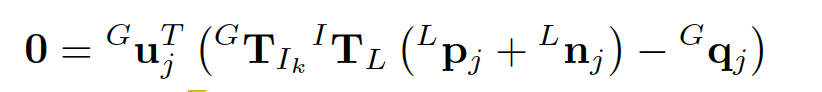
观测方程就把雷达数据和状态向量联系在一起了,如下所示。
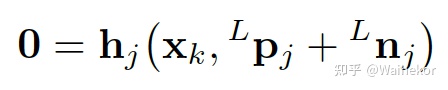
对于如何寻找最近地图中的边,或者平面,可以建立KD树搜索。通过构建残差方程,对于残差过大的激光点观测,我们就可以把它当成野值处理。
6.4. 迭代更新
我们建立的观测方程如下,其实和残差构建是一致的。
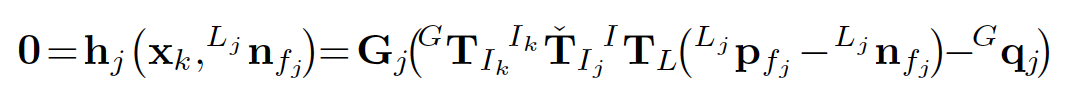
我们知道EKF需要做泰勒公式展开,求雅可比矩阵,如下所示:
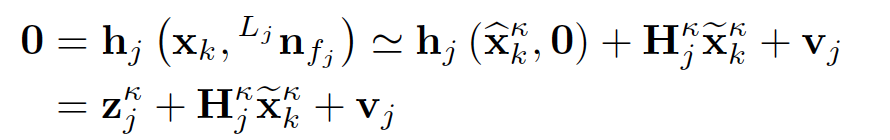
H矩阵就是对应的雅可比矩阵,文中提到下面两种计算增益的公式是等价的,第一个公式相比第二个公式,在计算效率上会更高。
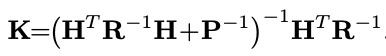

协方差的恶后验计算公式如下:
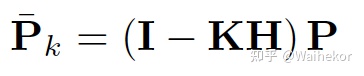
状态变量的后验如下:
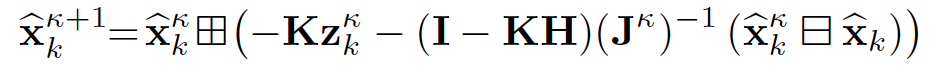
从最优化的角度来看滤波器,则IEKF的最优化公式如下:
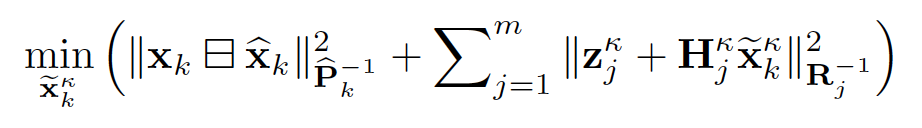
状态估计的整体流程如下,IEKF的迭代过程,有一个终止条件,就是看残差小于一个特定值。

7. 地图更新
地图更新过程就是把激光雷达点投影到世界坐标系的过程,如下公式所示:

8. 初始化
初始化需要静止2s,静止状态下可以计算陀螺仪的零偏,以及加速度计的重力向量。
9. 实验结果
如下所示,可以看到,相比LOAM以及LOAM+IMU的方案,FAST-LIO用时更短,并且LOAM+IMU是松耦合的方案。

从下图中可以看到,相比LOAM以及LOAM+IMU,FAST-LIO无论在慢速还是快速运动情况下,建图效果都更好。

参考文献
FAST-LIO(一):论文简要介绍 - 知乎
FAST-LIO: A Fast, Robust LiDAR-inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter