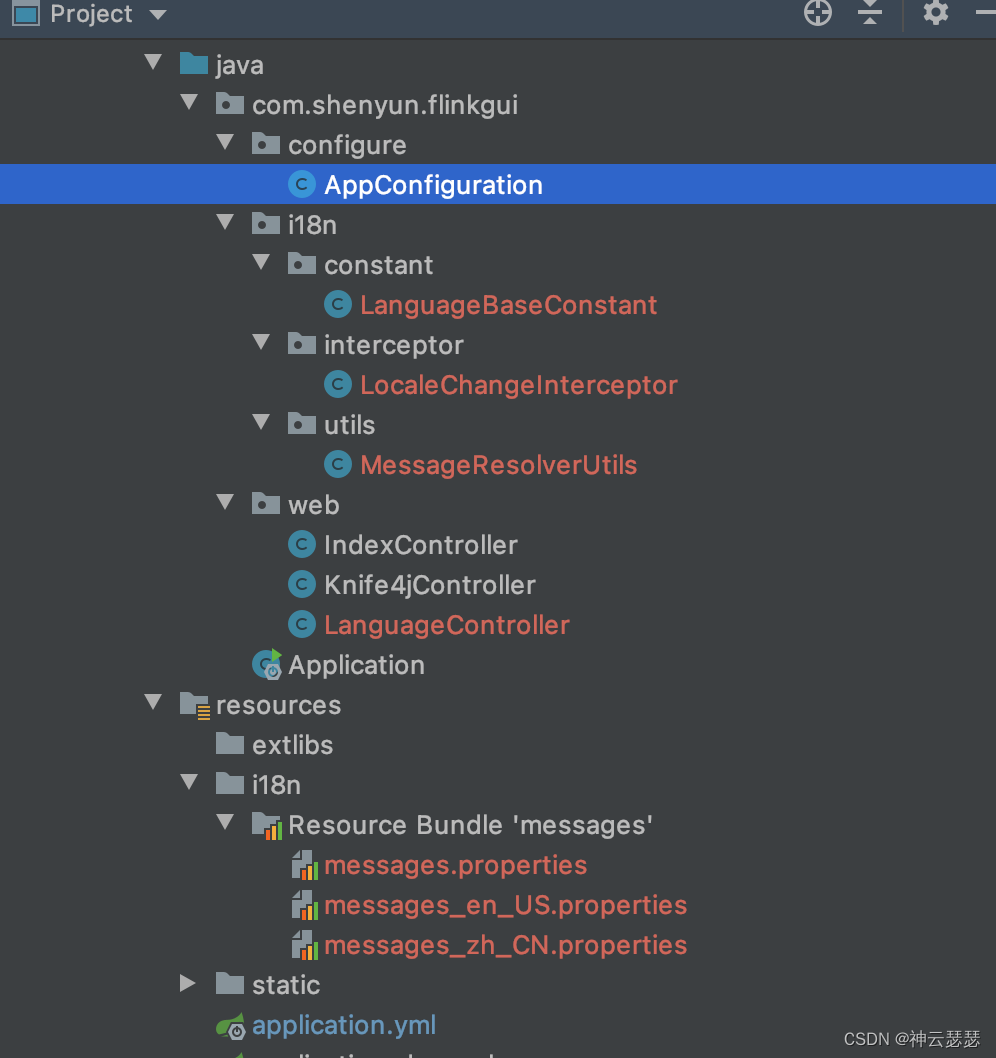
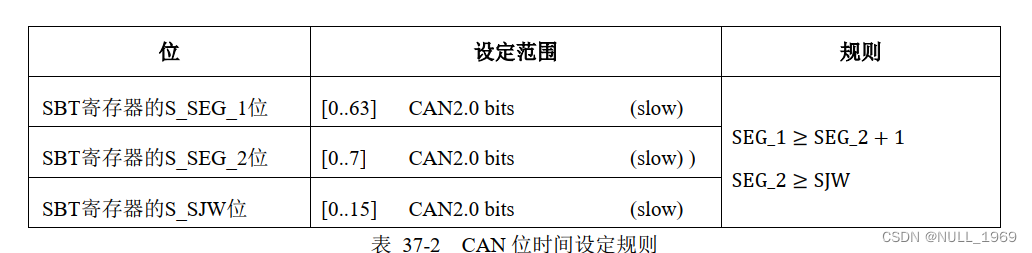
通过分析坐标轴中样本和样本间的距离可看到 2 个样本或 2 组样本间的差异性。若2个样本或2组样本之间的直线距离较近，则表示这2个样本或2组样本差异性较小；相反则表示差异性较大。因此PCA和PCoA 具有直观性(直接看两点之间的距离)和完整性(呈现所有样本)，数据易于分析解读。

PCA(Principal Components Analysis)，主成分分析，主分量分析或主成分回归分析法，

利用线性变换，将数据变换到新的坐标系统中，再利用降维的思想，使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上，第二大方差在第二个坐标(第二主成分)上。减少数据集维数，并保持数据集中方差最大的特征，使数据直观呈现在二维坐标系。

PCoA(Principal Co-ordinates Analysis)，主坐标分析，体现数据相似性或差异性的可视化坐标，是一种非约束性的数据降维分析方法，可研究样本组成的相似性或相异性。与PCA类似，通过一系列的特征值和特征向量进行排序后，选择主要排在前几位的特征值，找到距离矩阵中最主要的坐标，结果是数据矩阵的一个旋转，其没有改变样本点之间的相互位置关系，只是改变了坐标系统。

区别：

PCA是基于样本的相似系数矩阵(如：欧式距离)检索主成分；

PCoA是基于距离矩阵(欧式距离以外的其他距离)构成主坐标。

通过生物学的样例理解PCA：

假如有3个实验样本，共有1个物种x，用物种 x 的相对丰度表示样本和样本之间的差异。画一个一维坐标轴，将这3个样本的物种 x 的丰度表示在一维轴线上，如下图所示：

此时数据不发生偏移，样本和样本之间的距离代表样本之间的物种丰度差异(样本A和B间的距离即为A中的物种 x 的丰度与 B 中物种 x 的丰度的差值)。

假如有3个实验样本，共有2个物种：x 和 y。用物种 x 和物种 y 的相对丰度来在二维坐标系中定位样本。A=(x1,y1)， B=(x2,y2)，C=(x3,y3)，如下图所示：

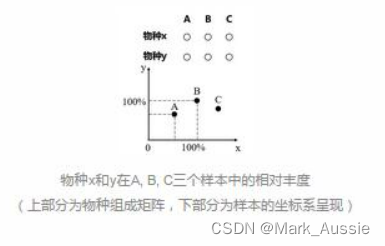
此时数据不发生偏移，样本和样本之间的距离代表样本之间的物种丰度差异。

假如有3个实验样本，共有k个物种: x, y, z…………k。可用物种x, y, z…………k的丰度来定位样本A=(x1,y1,z1……………k1)。样本B与C也可以用这种形式表示。A=(x1,y1,z1……………k1)是一组向量，而且是k维向量(A=(x1)是一维向量，A=(x1,y1)是二维向量，A=(x1,y1,z1)是三维向量)。但是k维向量无法在二维坐标系(平面)中表示(一维和二维向量可以，如上a和b两种情况)。此时将K维向量作出一些取舍，削去一些不重要的向量仅保留2个关键向量。

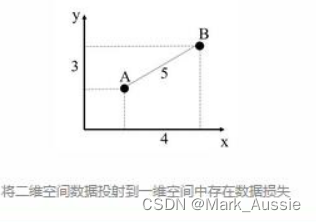
因降维处理，数据发生损失，样本和样本之间的距离代表样本之间的物种丰度差异。

通过生物学的样例理解PCoA：

假如有2个实验样本，有很多物种，用某中算法计算每个样本的物种组成差异度(用一个数值表示物种相对丰度)，数值之间的差异就代表了2个样本的物种相对丰度的差异。画一个一维坐标轴，将这2个样本表示在一维轴线上，如下图所示：

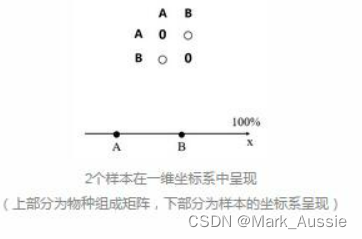
此时数据不发生偏移，样本和样本之间的距离代表样本之间的物种丰度差异。

假如有3个实验样本，用某种算法计算每个样本的物种组成差异度(用一个数值表示物种相对丰度)，数值之间的差异就代表了每2个样本的物种相对丰度的差异。画一个二维坐标轴(三点组成一个面)，将这3个样本表示在二维轴线上，如下图所示：

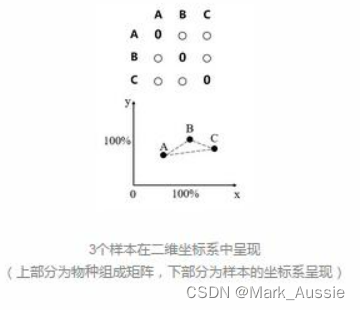
此时数据不发生偏移，样本和样本之间的距离代表样本之间的物种丰度差异。

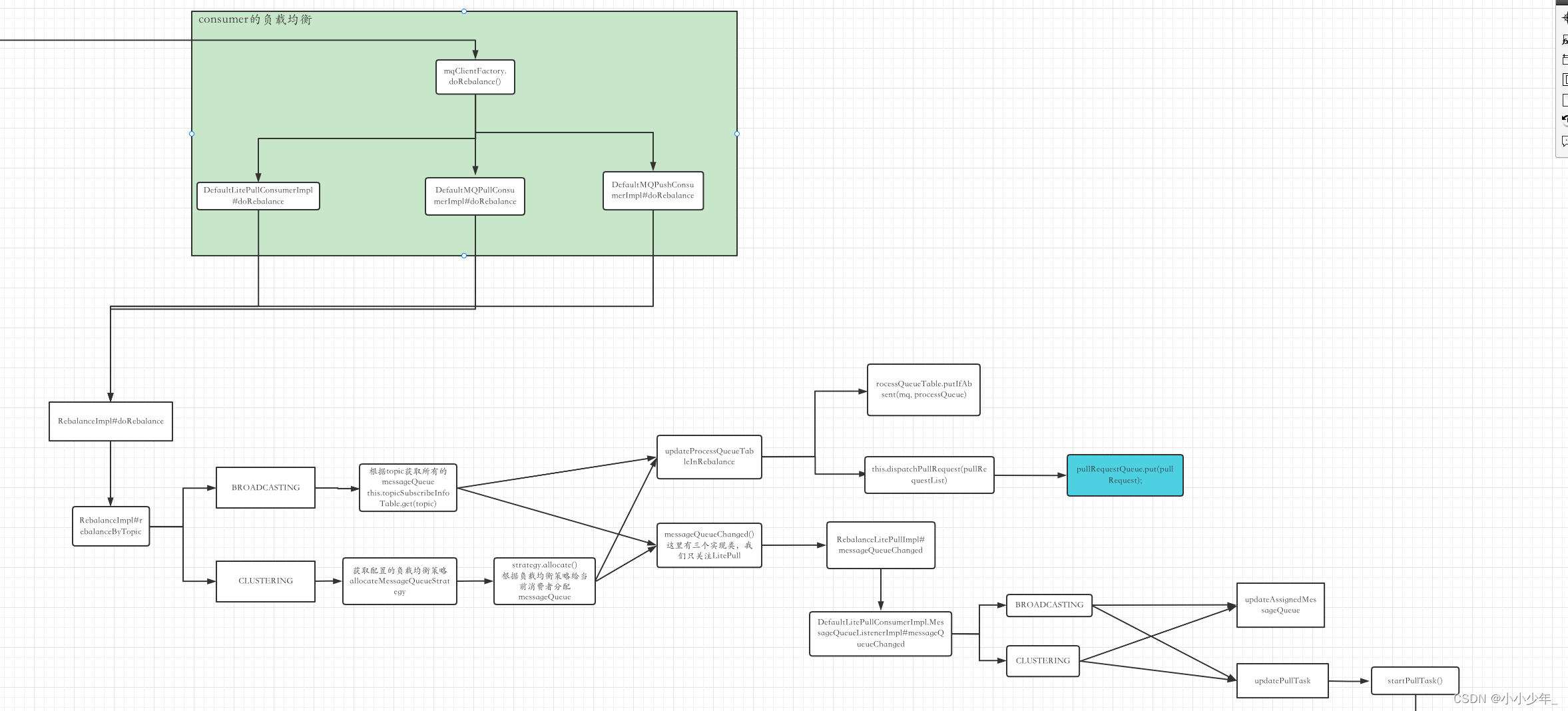
假如有n个实验样本，用某种算法计算每个样本的物种组成差异度(用一个数值表示物种相对丰度)，数值之间的差异就代表了每2个样本的物种相对丰度的差异。画一个n-1维坐标轴，将这n个样本表示在n-1维空间中。但是n-1维空间无法在平面上表示(一维和二维除外，三维勉强可以)，因此只能利用矩阵呈现，如下图所示：

若要将n-1维的数据在二维坐标系中呈现，需降维处理，即将n-1维的数据投影到二维空间当中，方法与思路同PCA类似。此时，2个坐标轴的贡献率均小于100%，如下图所示：

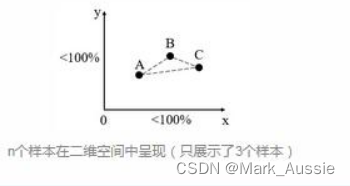
因降维处理，数据发生损失，样本和样本之间的距离代表样本之间的物种丰度差异。

“PCA是基于样本的相似系数矩阵(如欧式距离)来寻找主成分，而PCoA是基于距离矩阵(欧式距离以外的其他距离)来寻找主坐标”，其实浅显地来理解，就是上面这么回事。

参考：

三文读懂PCA和PCoA(一)