霍夫变换的基本原理
霍夫变换(Hough Transform)可以理解为图像处理中的一种特征提取技术,通过投票算法检测具有特定形状的物体。霍夫变换运用两个坐标空间之间的变换将在一个空间中具有相同形状的曲线或直线映射到另一个坐标空间中的一个点形成峰值,从而把检测任意形状的问题转化为统计峰值问题。(把这句话背下来吧)
直线检测
背景知识
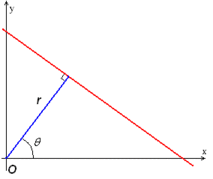
高中的时候我们都学过笛卡尔坐标系 (x, y) 也就是直角坐标系,在这个坐标系中可以有很多种方法来表示一条直线,例如点斜式 y − b = k ∗ ( x − a ) y - b = k*(x - a) y−b=k∗(x−a) 或者两点式 y − y 2 = y 1 − y 2 x 1 − x 2 ∗ ( x − x 2 ) y - y_2 = \frac{y_1 - y_2}{x_1 - x_2}*(x - x_2) y−y2=x1−x2y1−y2∗(x−x2) ,但是在霍夫变换中我们使用的是另外一种表示方法即极坐标系,使用两个变量 ( r , θ ) (r, \theta) (r,θ) 来表示一条直线,具体地 r r r 为一条直线到原点的距离, θ \theta θ 为该直线的垂线与 x 轴的夹角。
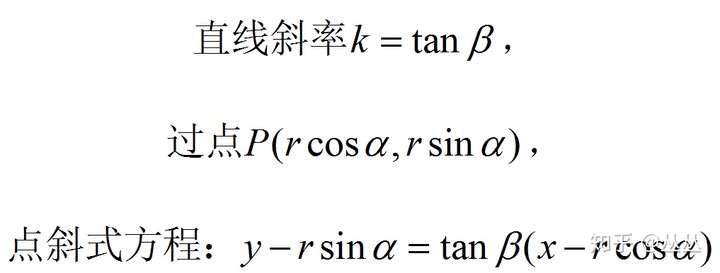
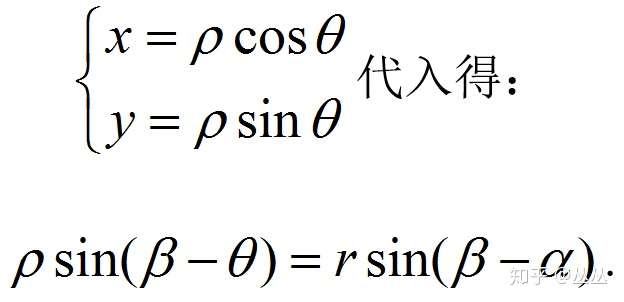
hough变换检测直线的流程
怎么来检测一条直线呢?我们可以取需要检测的图像上的 N 个点,为每个点假设 n 个方向的直线(空间中经过一个点的直线有无数条),通常 n = 180 ,分别计算这 n 条直线的 ( r , θ ) (r, \theta) (r,θ) 坐标,既可以得到 n 个坐标,N 个点就是 N*n 个 ( r , θ ) (r, \theta) (r,θ) 坐标。
那么如果有多个点在一条直线上,那么这几个点在 θ \theta θ 的某个取值 θ i \theta_i θi 处的 r i r_i ri 相等,如果图中只有这条直线的话,那么 θ = θ i \theta = \theta_i θ=θi 时的 $r_i $ 的统计量是最多的,找到这个 θ i \theta_i θi 就意味着找到了这条直线。
拓展到一张图中有多条直线的情况,我们可以设置一个阈值来选择前 k 个统计量的 ( r i , θ i ) (r_i, \theta_i) (ri,θi) 来检测 k 条直线。当然还有相邻两条直线的拼接或者长度要超过某个阈值的直线才需要输出的问题,这些就要看怎么去实现了,不是我们这篇文章的要点,这些功能在 opencv 中都有实现,需要的可以去了解。
下面拿一个博客中的例子来说明:
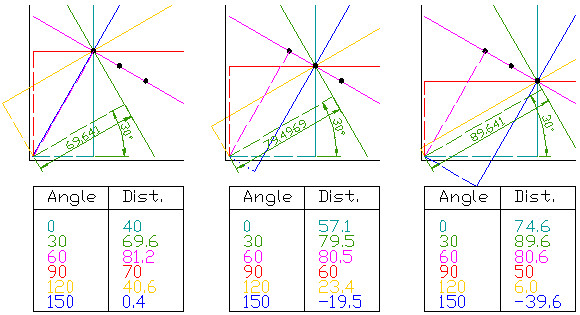
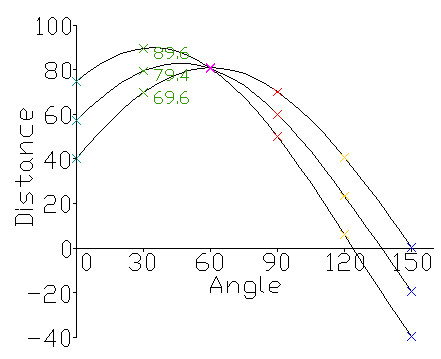
如果空间中有3个点,如何判断这三个点在不在一个直线上?这个例子中,对于每个点均求过该点的6条直线的 ( r , θ ) (r,\theta) (r,θ) 坐标,共求了3*6个 ( r , θ ) (r,\theta) (r,θ) 坐标。可以发现在 θ = 60 \theta = 60 θ=60 时,三个点的 r 都近似为80.7,由此可判定这三个点都在直线(80.7,60)上。
通过 ( r , θ ) (r, \theta) (r,θ) 坐标系可以更直观表示这种关系,如果对于一个给定点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0) ,我们在极坐标系下画出经过该点的所有直线的极坐标表示,将得到一条正弦曲线。下图是直角坐标系下的三个点在极坐标系下绘出的图:图中三个点的 ( r , θ ) (r, \theta) (r,θ) 曲线汇集在一起,该交点就是同时经过这三个点的直线。
hough变换检测圆的流程
检测直线的时候我们使用 ( r , θ ) (r, \theta) (r,θ) 来表示一条直线,在检测圆时我们是使用 ( a , b , r ) (a,b,r) (a,b,r) 来表示确定一个圆心为 ( a , b ) (a,b) (a,b) 半径为 r r r 的圆。
当某个圆过点 ( x , y ) (x,y) (x,y) 时,满足 ( x − a ) 2 + ( y − b ) = r 2 (x - a)^2 + (y - b) = r^2 (x−a)2+(y−b)=r2 ,所以过点 ( x , y ) (x,y) (x,y) 的所有圆可以表示为 ( a ( i ) , b ( i ) , r ( i ) ) (a^{(i)},b^{(i)}, r^{(i)}) (a(i),b(i),r(i)) 。与上面检测直线的原理一样,要检测三个点是否在同一个圆上,首先计算过第一个点的所有圆表示为 ( a 1 ( i ) , b 1 ( i ) , r 1 ( i ) ) (a_1^{(i)},b_1^{(i)}, r_1^{(i)}) (a1(i),b1(i),r1(i)) ,过第二个点的所有圆表示为 ( a 2 ( i ) , b 2 ( i ) , r 2 ( i ) ) (a_2^{(i)},b_2^{(i)}, r_2^{(i)}) (a2(i),b2(i),r2(i)) ,过第三个点的所有圆表示为 ( a 3 ( i ) , b 3 ( i ) , r 3 ( i ) ) (a_3^{(i)},b_3^{(i)}, r_3^{(i)}) (a3(i),b3(i),r3(i)) ,如果这三个点在同一个圆上,那么存在一个值 ( a k , b k , r k ) (a_k, b_k, r_k) (ak,bk,rk) 是三个点的所有圆表示中都存在的,也就是说这三个点同时在圆 ( a k , b k , r k ) (a_k, b_k, r_k) (ak,bk,rk) 上。
下面借助这张图来形象理解:
先说说怎么表示过点
(
x
1
,
y
1
)
(x_1, y_1)
(x1,y1) 的所有圆的表示。当
r
1
r_1
r1 确定时,根据 $(x_1 - a_1)^2 + (y_1 - b_1) = r_1^2 $ ,即
(
a
1
,
b
1
)
(a_1,b_1)
(a1,b1) 的轨迹则变成了以
(
x
1
,
y
1
)
(x_1, y_1)
(x1,y1) 为圆心
r
1
r_1
r1 为半径的圆,取完所有的
r
1
i
r_1^i
r1i ,
(
a
1
(
i
)
,
b
1
(
i
)
,
r
1
(
i
)
)
(a_1^{(i)},b_1^{(i)}, r_1^{(i)})
(a1(i),b1(i),r1(i)) 的轨迹便如图中的一个圆锥,三个点的所有圆表示形成的圆锥的交点 A 所对应的那个
(
a
k
,
b
k
,
r
k
)
(a_k, b_k, r_k)
(ak,bk,rk) 便是经过这三个点的圆。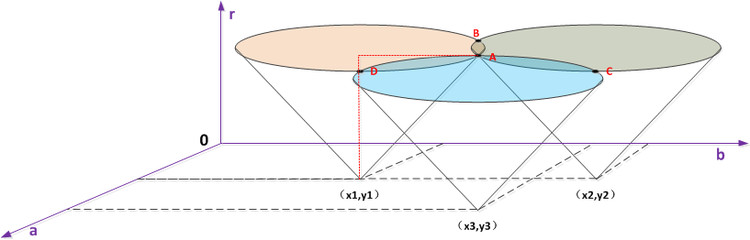
椭圆或者其他形状同理,只要找到一种表示即可将在一个空间中的形状问题变换到另一个空间的点统计问题。
拓展
图像处理中,在使用霍夫线变换之前,要首先对图像进行边缘检测,即霍夫线变换的直接输入只能是边缘二值图像。
参考资料
Hough变换检测原理
![[附源码]Python计算机毕业设计高校教务管理系统Django(程序+LW)](https://img-blog.csdnimg.cn/2f8537bff50a4b24afd61e2ca8e6d550.png)