1.定义
2.例题
3.使用软件及解题

一、定义

1.整数规划（Integer Programming，简称IP）：是一种数学优化问题，它是线性规划（Linear Programming，简称LP）的一个扩展形式。在线性规划中，优化目标和约束条件都是线性的，而在整数规划中，除了这些线性约束外，变量还被限制为整数值。在整数规划问题中，我们需要在给定一组变量和一组线性约束条件的情况下，找到满足这些约束条件的整数值变量，使得一个特定的线性目标函数达到最大或最小。整数规划在实际问题中具有广泛的应用，例如生产调度、资源分配、物流规划、项目排程等。

2.与线性规划相比
  整数规划问题更为复杂，因为整数变量引入了离散性，使得问题的解空间不再是连续的。这导致整数规划问题通常更难以求解，因为搜索整数解的空间相对于连续解的空间更大且不连续。

  求解整数规划问题，需要使用专门的算法和工具，如分支定界法、割平面法、混合整数线性规划求解器等。这些方法通常会尝试在搜索整数解的过程中通过一系列的策略来逐渐缩小解空间，以找到最优的整数解。

3.整数规划分类（根据不同的特性和约束条件）

（1） 0-1整数规划：在这种问题中，变量被限制为取值为0或1，表示是否选择某个决策。这类问题的典型应用包括装载问题、投资决策问题等。

（2） 混合整数线性规划：在这类问题中，除了一部分变量可以取连续值外，还有一部分变量需要取整数值。MILP问题广泛应用于生产计划、物流网络优化等领域。

（3） 纯整数规划：所有的变量都必须取整数值，没有连续变量。这类问题在排产、任务分配等领域中常见。

（4） 多目标整数规划：在这种问题中，有多个优化目标需要同时考虑。这样的问题在多目标决策中很有用，例如平衡成本和资源利用率。

（5） 分支限界整数规划：这是一种常用的求解整数规划问题的方法。它通过逐步分解问题，并在每个分支上进行线性规划求解，然后根据解的上下界限制来确定是否进一步探索该分支。

（6） 割平面整数规划：在这种方法中，通过添加一系列的割平面约束来逐步缩小整数解空间，以逼近最优解。割平面法常用于求解MILP问题。

（7） 约束编程：这是一种用于求解离散优化问题的方法，它不仅适用于整数规划，还适用于更广泛的约束满足问题。在约束编程中，问题的变量和约束条件都可以具有不同的性质，如整数、集合等。

4.整数规划问题一般求解过程步骤

1.建立数学模型：

（1）确定决策变量：确定需要优化的变量，以及这些变量的含义和范围。
（2）确定目标函数：定义需要最大化或最小化的目标函数，通常是线性组合的形式。
（3）确定约束条件：列出问题的约束条件，这些条件限制了变量之间的关系。

2.线性规划求解：

（1）将整数规划问题转化为相应的线性规划问题，即将所有变量视为连续变量。
（2）使用线性规划求解器（如单纯形法、内点法等）求解得到线性规划的最优解。

3.检查解的整数性：

（1）如果线性规划的最优解是整数，那么整数规划问题的解已经找到，问题解决。
（2）如果线性规划的最优解不是整数，就需要继续进行下面的步骤。

4.分支定界法：

（1）选择一个分支变量：选择一个在线性规划解中取非整数值的变量作为分支变量。
（2）拆分问题：将问题分为两个子问题，一个限制该分支变量为下取整，另一个限制为上取整。
（3）对每个子问题重复求解的过程，直到找到整数解或者发现问题无解为止。
（4）在每次求解子问题时，可以使用割平面、启发式等方法来改善求解效率。

5.终止条件：

（1）当找到整数解时，检查是否比当前最优解更优，更新最优解。
（2）**当发现所有分支问题都没有整数解，或者问题的最优解已经被找到，终止求解过程。

6.输出结果：

返回找到的最优整数解或者近似整数解作为问题的解决方案。

5.求解方法分类及定义

(1)）分枝定界法一可求纯或混合整数线性规划
  对有约束条件的最优化问题（其可行解为有限数）的所有可行解空间恰当地进行系统搜索，这就是分枝与定界内容。通常，把全部可行解空间反复地分割为越来越小的子集，称为分枝；并且对每个子集内的解集计算一个目标下界（对于最小值问题），这称为定界。在每次分枝后，凡是界限超出已知可行解集目标值的那些子集不再进一步分枝，这样，许多子集可不予考虑，这称剪枝。

(2）割平面法—可求纯或混合整数线性规划。
(3）隐枚举法—求解0-1”整数规划。
过滤隐枚举法
分枝隐枚举法
(4)匈牙利法一解决指派问题(“0-1"规划特殊情形)。
(5）蒙特卡洛法—求解各种类型规划。

二、例题

1.分枝定界法

三、使用软件及解题

1.matlab求解

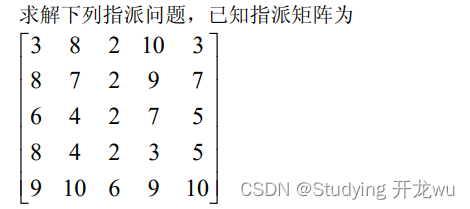
解法一：编写 Matlab 程序如下：

c=[3 8 2 10 3;8 7 2 9 7;6 4 2 7 5
   8 4 2 3 5;9 10 6 9 10];
c=c(:);
a=zeros(10,25);
for i=1:5
   a(i,(i-1)*5+1:5*i)=1;
   a(5+i,i:5:25)=1;
end
b=ones(10,1);
[x,fval]=bintprog(c,[],[],a,b);
x=reshape(x,[5,5]), fval

2.1.LINGO求解
求解法二：的LINGO程序如下

model:
sets:
var/1..5/;
link(var,var):c,x;
endsets
data:
c=3 8 2 10 3
  8 7 2 9 7
  6 4 2 7 5
  8 4 2 3 5
  9 10 6 9 10;
enddata
min=@sum(link:c*x);
@for(var(i):@sum(var(j):x(i,j))=1);
@for(var(j):@sum(var(i):x(i,j))=1);
@for(link:@bin(x));
end