1.题目链接：

70. 爬楼梯

2.解题思路：

2.1.题目要求：

给个阶数 n，要求返回爬完 n 阶有几种方法。

一次可以爬 1 步或者 2 步。

示例 1
输入：n = 1 
输出：1
解释：有一种方法可以爬到楼顶。 
1. 1 阶

示例 2
输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例 3
输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

示例 4
输入：n = 4
输出：5
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶 + 1 阶 
2. 1 阶 + 1 阶 + 2 阶
3. 1 阶 + 2 阶 + 1 阶
4. 2 阶 + 1 阶 + 1 阶
5. 2 阶 + 2 阶

2.2.思路：

根据示例1234，发现一个规律，n = 3 的方法总数 " 3 " 是 n =2 和 n=1 的方法总数之和，n = 4 同理，所以推论，从 n = 3开始，后一项的方法总数是前两项方法总数之和。

（注意 n = 0不存在，因为不可能一阶楼梯没走就到一层了）

1 2 3 5 8 类比斐波那契数列

2.3.动规五部曲：

2.3.1.确定dp数组以及下标的含义

dp[ i ] 的意思是，爬到第 i 层楼梯的时候，有 dp[ i ] 种爬法。

2.3.2.确定递推公式

推论，从 n = 3开始，后一项的方法总数是前两项方法总数之和。（注意 n = 0不存在）

及 dp[ i ] = dp[ i-1 ] + dp[ i-2 ]

2.3.3.dp数组如何初始化

n = 0 不存在的条件限制 dp数组，只能从i = 1 开始初始化。

所以初始化 dp[ 1 ] = 1 , dp[ 2 ] = 2 。

2.3.4.确定遍历顺序

由 dp[ i-1 ] ， dp[ i-2 ] 这样的后两项，来推导 dp [ i ] 这样的前一项，所以遍历顺序由前向后遍历

2.3.5.举例推导dp数组

举例当n为5的时候，dp table（dp数组）应该是这样的

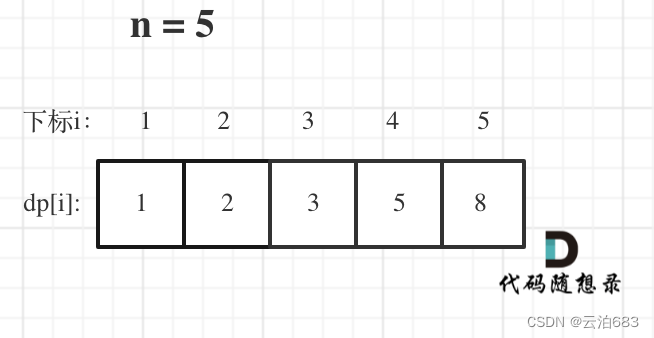
如果代码出问题了，就把dp table 打印出来，看看究竟是不是和自己推导的一样。

2.4.总代码：

初始版

//版本一
class Solution {
public:
    int climbStairs(int n) {
        if (n <= 1) return n; // 因为下面直接对dp[2]操作了，防止空指针
        vector<int> dp(n + 1);
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) { // 注意i是从3开始的
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
};

优化版

// 版本二
class Solution {
public:
    int climbStairs(int n) {
        if (n <= 1) return n;
        int dp[3];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            int sum = dp[1] + dp[2];
            dp[1] = dp[2];
            dp[2] = sum;
        }
        return dp[2];
    }
};