Kaggle竞赛——Titanic泰坦尼克之灾（保姆级基础版）

Kaggle竞赛网址：https://www.kaggle.com/c/titanic

本次Kaggle泰坦尼克之灾分析过程大致分为：

第1步：了解数据
第2步：分析数据之间的关系
第3步：缺失项数据处理
第4步：特征因子化
第5步：处理特殊值或浮动较大的数值
第6步：数据筛选
第7步：数据建模
第8步：测试集预处理
第9步：结果预测
第10步：模型优化（下一章讲）
第11步：模型融合（下一章讲）

函数总结——涉及到的函数

pandas包
DataFrame(简写df)
pd.read_csv()
pd.get_dumines(data, prefix)
pd.concat(data, axis)
df.notnull()
df.isnull()
df.as_matrix()
df.loc()
df.drop(data, axis, inplace)
df.filter(regex)
df.index
df.sort_index()
df.sort_values()
numpy包
np.astype()
np.int32()
sklearn包
ensemble模块中的RandForestRegressor算法(简写rfr)
rfr.fit()
rfr.predict()
preprocessing模块中的StandardScaler()函数(简写scalar)
scalar.fit()
scalar.fit().transform()
linear_model模块中的LogisticRegression算法(简写clf)
clf.fit()
clf.predict()
matplotlib包
涉及的有点多，此处省略。

# 处理警告信息
import warnings
warnings.filterwarnings("ignore", message = "numpy.dtype size changed")

import pandas as pd # 数据分析
import numpy as np # 科学计算
from pandas import Series, DataFrame

data_train = pd.read_csv("train.csv")
data_train.columns 
# data_train[data_train.Cabin.notnull()]['Survived'].value_counts()

在这里插入图片描述
第1步：了解数据
用excel查看csv文件中的数据，并依据kaggle里面的提示

1.1 大概有以下这些字段
PassengerId => 乘客ID（唯一标识）
Survived => 幸存情况（0：遇难，1：幸存）
Pclass => 乘客等级 (1/2/3等舱位)
Name => 乘客姓名
Sex => 性别
Age => 年龄
SibSp => 堂兄弟/妹个数
Parch => 父母与小孩个数
Ticket => 船票信息
Fare => 票价
Cabin => 客舱
Embarked => 登船港口（S/C/Q港口）

data_train.info()

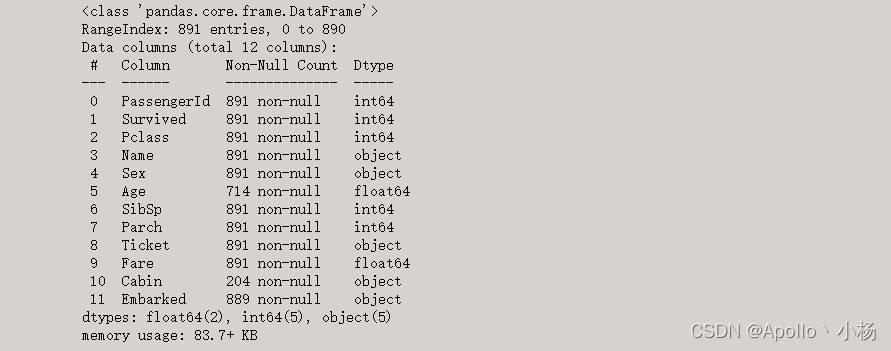
在这里插入图片描述
1.2 数据基本情况
训练数据中总共有891名乘客，但有些属性的数据不全。
比如：Age（年龄）属性只有714名乘客有记录
Cabin（客舱）仅有204名乘客是已知的
总共有5个object类的字段需要进行处理

 data_train.describe()

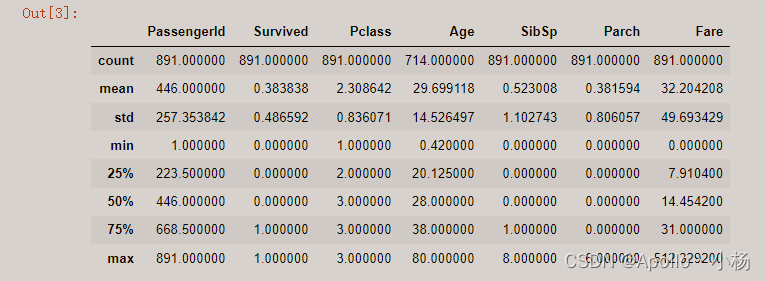
在这里插入图片描述
mean行的数据告诉我们：
a. Survived字段中大概有0.383838的人最后获救了；
b. 2和3等舱的人数比1等舱要多；
c. 有数据,已知年龄的乘客，平均年龄大概是29.7岁。

第2步：分析数据之间的关系
这部分主要是结合数据可视化的方式进行分析，数据分析的目有两个。一是分析有缺失值的属性和其他属性的关系，填补缺失值；二是分析Survived和其他属性之间的关系。

2.1 获救情况
2.2 乘客等级分布
2.3 按年龄看获救分布 (1为获救)
2.4 各等级的乘客年龄分布
2.5 各登船口岸上船人数

import matplotlib.pyplot as plt

#中文支持
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

fig = plt.figure()
fig.set(alpha=0.2)  # 设定图表颜色alpha参数

plt.subplot2grid((2,3),(0,0))             # 在一张大图里分列几个小图
data_train.Survived.value_counts().plot(kind='bar')# 绘制存活者与非存活者的柱状图
plt.title(u"获救情况 (1为获救)") # 标题
plt.ylabel(u"人数")  

plt.subplot2grid((2,3),(0,1))
data_train.Pclass.value_counts().plot(kind="bar")
plt.ylabel(u"人数")
plt.title(u"乘客等级分布")

plt.subplot2grid((2,3),(0,2))
plt.scatter(data_train.Survived, data_train.Age)
plt.ylabel(u"年龄")                         # y轴标签
plt.grid(b=True, which='major', axis='y') # 格式化图表的网格线样式
plt.title(u"按年龄看获救分布 (1为获救)")


plt.subplot2grid((2,3),(1,0), colspan=2)
data_train.Age[data_train.Pclass == 1].plot(kind='kde')   # 绘制1等舱乘客年龄的密度
data_train.Age[data_train.Pclass == 2].plot(kind='kde')
data_train.Age[data_train.Pclass == 3].plot(kind='kde')
plt.xlabel(u"年龄")# plots an axis lable
plt.ylabel(u"密度") 
plt.title(u"各等级的乘客年龄分布")
plt.legend((u'头等舱', u'2等舱',u'3等舱'),loc='best') # 图表设置图例


plt.subplot2grid((2,3),(1,2))
data_train.Embarked.value_counts().plot(kind='bar')
plt.title(u"各登船口岸上船人数")
plt.ylabel(u"人数")  

plt.subplots_adjust(hspace=0.5, wspace=0.5) # 调整图之间的间距
plt.show()

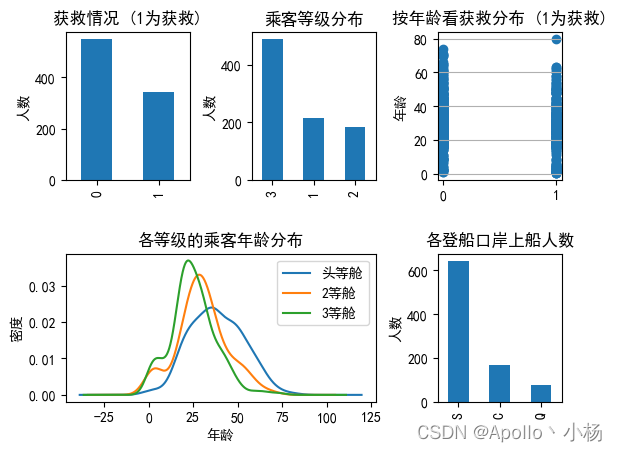
在这里插入图片描述
从图中可以看出：
a. 被救的人300多个，不到总人数的一半；
b. 3等舱获救的乘客最多，其次是1、2等舱；
c. 遇难和获救的人年龄跨度都很广；
d. 3个舱的年龄总体趋势差不多，2和3等舱乘客20-25岁的最多，1等舱35-40岁的最多；
e. 登船港口人数按照S、C、Q递减，而且S港口的人数远高于另外两个港口的人数。

猜想
不同舱位、乘客等级可能和个人的财富、地位有关系，最后获救概率可能会不一样；
基于电影中的台词“小孩和女士先走”，年龄对获救概率一定是有影响，可以作为特征看看；
登船港口是否与出身地位不同有关系？

2.6 各乘客等级的获救情况
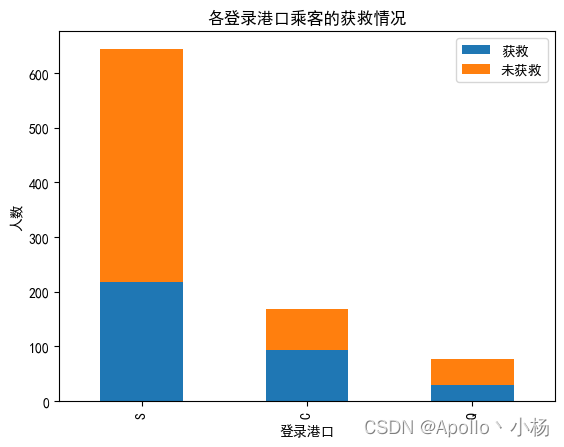
2.7 各登录港口的获救情况
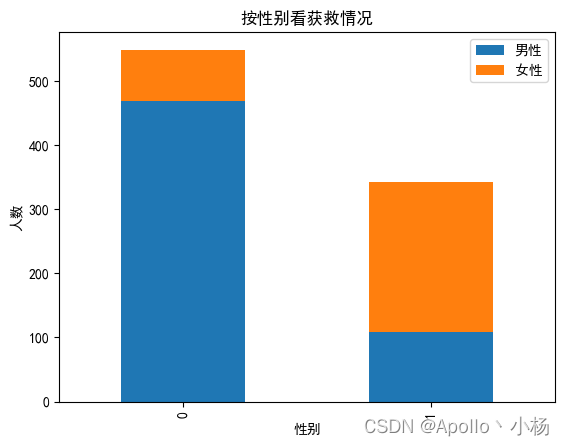
2.8 各性别的获救情况
2.9 根据各乘客等级和性别的获救情况

# 各乘客等级的获救情况
fig = plt.figure()
fig.set(alpha=0.2)  # 设定图表颜色alpha参数

Survived_0 = data_train.Pclass[data_train.Survived == 0].value_counts()
Survived_1 = data_train.Pclass[data_train.Survived == 1].value_counts()

df=pd.DataFrame({u'获救':Survived_1, u'未获救':Survived_0})
df.plot(kind='bar', stacked=True)

plt.title(u"各乘客等级的获救情况")
plt.xlabel(u"乘客等级") 
plt.ylabel(u"人数") 
plt.show()

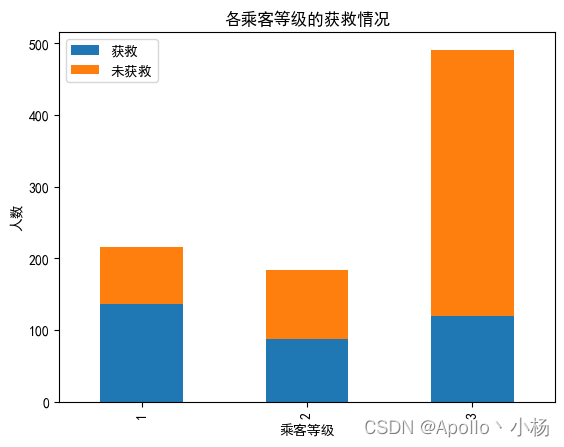
在这里插入图片描述

# 各登录港口的获救情况
fig = plt.figure()
fig.set(alpha=0.2)  # 设定图表颜色alpha参数

Survived_0 = data_train.Embarked[data_train.Survived == 0].value_counts()
Survived_1 = data_train.Embarked[data_train.Survived == 1].value_counts()
df=pd.DataFrame({u'获救':Survived_1, u'未获救':Survived_0})
df.plot(kind='bar', stacked=True)
plt.title(u"各登录港口乘客的获救情况")
plt.xlabel(u"登录港口") 
plt.ylabel(u"人数") 

plt.show()

在这里插入图片描述

# 各性别的获救情况
fig = plt.figure()
fig.set(alpha=0.2)  # 设定图表颜色alpha参数

Survived_m = data_train.Survived[data_train.Sex == 'male'].value_counts()
Survived_f = data_train.Survived[data_train.Sex == 'female'].value_counts()
df=pd.DataFrame({u'男性':Survived_m, u'女性':Survived_f})
df.plot(kind='bar', stacked=True)
plt.title(u"按性别看获救情况")
plt.xlabel(u"性别") 
plt.ylabel(u"人数")
plt.show()

在这里插入图片描述

# 根据各乘客等级和性别的获救情况
S1 = data_train.Sex
S2 = data_train.Pclass
S3 = data_train.Survived

plt.subplot(141)
plt.bar([0,1], S3[S1=='female'][S2!=3].value_counts(), color='#FA2479', width=.5)
plt.xticks([0,1],[u'获救',u'未获救'])
plt.xlim([-.5,1.5])
plt.yticks(range(0,350,100))
plt.legend([u"女性/高级舱"], loc='best')

plt.subplot(142)
plt.bar([0,1], S3[S1=='female'][S2==3].value_counts(), color='pink', width=.5)
plt.xticks([0,1],[u'获救',u'未获救'])
plt.xlim([-.5,1.5])
plt.yticks(range(0,350,100))
plt.legend([u"女性/低级舱"], loc='best')
plt.title(u"根据各乘客等级和性别的获救情况")

plt.subplot(143)
plt.bar([0,1], S3[S1=='male'][S2!=3].value_counts(), color='steelblue', width=.5)
plt.xticks([0,1],[u'获救',u'未获救'])
plt.xlim([-.5,1.5])
plt.yticks(range(0,350,100))
plt.legend([u"男性/高级舱"], loc='best')

plt.subplot(144)
plt.bar([1,0], S3[S1=='male'][S2==3].value_counts(), color='lightblue', width=.5)
plt.xticks([1,0],[u'未获救',u'获救'])
plt.xlim([-.5,1.5])
plt.yticks(range(0,350,100))
plt.legend([u"男性/低级舱"], loc='best')

plt.show()

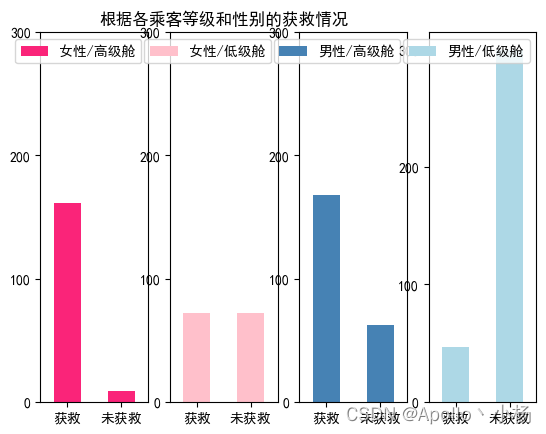
在这里插入图片描述
从上述四个图中可以看出
a. 从各乘客等级的获救情况来看：头等舱和2等舱乘客的幸存概率相对高一些，可以作为特征看看； b. 从各登录港口的获救情况来看：S港口人数最多，Q港口人数最少，但生存率都在三分之一左右，C港口的获救人数过半，需要进一步验证，受什么因素影响。性别还是船舱等级？
c. 从性别来看获救情况：女性获救的概率显然高于男性，因此可作为重要特征；
d. 从各乘客等级和性别的获救情况来看：高级船舱对生存率的影响要比性别的略高。

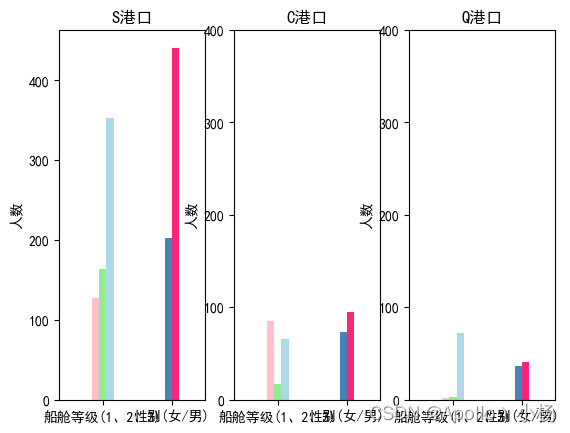
2.10 不同港口的船舱等级、性别情况
2.11 不同港口的年龄分布
2.12 船票费用和生存的关系
2.13 兄妹&配偶数和生存的关系

# 不同港口的船舱等级、性别情况
S=data_train.Embarked
S1=data_train.Pclass
S2=data_train.Sex
plt.subplot(131)
plt.title(u'S港口')
plt.bar([0.5,0.6,0.7],S1[S=='S'].value_counts().sort_index(),width=0.1,color=['pink','lightgreen','lightblue'])
plt.bar([1.5,1.6],S2[S=='S'].value_counts().sort_index(),width=0.1,color=['steelblue','#FA2479'])
plt.xlim([0,2])
plt.xticks([0.6,1.55],[u'船舱等级(1、2、3)',u'性别(女/男)'])
plt.yticks(range(0,500,100))
plt.ylabel(u'人数')

plt.subplot(132)
plt.title(u'C港口')
plt.bar([0.5,0.6,0.7],S1[S=='C'].value_counts().sort_index(),width=0.1,color=['pink','lightgreen','lightblue'])
plt.bar([1.5,1.6],S2[S=='C'].value_counts().sort_index(),width=0.1,color=['steelblue','#FA2479'])
plt.xlim([0,2])
plt.xticks([0.6,1.55],[u'船舱等级(1、2、3)',u'性别(女/男)'])
plt.yticks(range(0,500,100))
plt.ylabel(u'人数')

plt.subplot(133)
plt.title(u'Q港口')
plt.bar([0.5,0.6,0.7],S1[S=='Q'].value_counts().sort_index(),width=0.1,color=['pink','lightgreen','lightblue'])
plt.bar([1.5,1.6],S2[S=='Q'].value_counts().sort_index(),width=0.1,color=['steelblue','#FA2479'])
plt.xlim([0,2])
plt.xticks([0.6,1.55],[u'船舱等级(1、2、3)',u'性别(女/男)'])
plt.yticks(range(0,500,100))
plt.ylabel(u'人数')

plt.show()

在这里插入图片描述

# 不同等级船舱的年龄分布
S1=data_train.Age
S2=data_train.Embarked
S1[S2=='S'].plot(kind='kde', label='S')
S1[S2=='C'].plot(kind='kde', label='C')
S1[S2=='Q'].plot(kind='kde', label='Q')
plt.xlabel('年龄',size=14)
plt.ylabel('')
plt.legend()
plt.title('不同等级船舱的年龄分布', size=14)
plt.show()

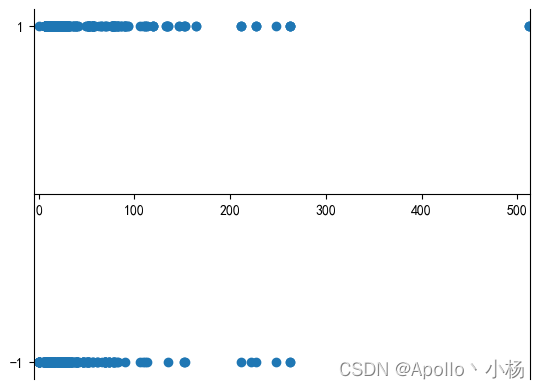
在这里插入图片描述

# 船票费用和生存的关系
S=data_train.sort_values('Fare')
S1=S.Survived
S2=S.Fare
S1.loc[S1==0]=-1
# print(S1)
# print(S2)
plt.scatter(S2,S1)
plt.xlim([-5,513])
plt.yticks([-1,1])
ax=plt.gca()
ax.spines['bottom'].set_position(('data',0))
ax.spines['top'].set_color('none')
plt.show()

在这里插入图片描述

S=data_train
S1=S.Survived
S2=S.SibSp[S1==1].value_counts().sort_index()
S3=S.SibSp[S1==0].value_counts().sort_index()
#print(S2)
#print(S3)
plt.bar(S2.index,S2,width=.4)
plt.bar(S3.index,-S3,width=.4)
plt.xticks(range(0,9))
ax=plt.gca()
ax.spines['bottom'].set_position(('data',0))
ax.spines['top'].set_color('none')
plt.title('兄妹&配偶数和生存的关系')
plt.show()

在这里插入图片描述
从上述四个图中可以看出
a. 从不同港口的船舱等级、性别情况来看：性别和港口无关，但是船舱等级好像没有太大规律可言，Q港口基本上是三等舱的，C港口二等舱较少；
b. 从不同港口的年龄分布来看：不同港口的年龄也分布差不多，所以综上港口不大适合作为一个主要特征，先作为一个备选特征；
c. 从船票费用和生存的关系来看：好像没有太大关系，不是主要特征，作为备选特征；
d. 从兄妹&配偶数和生存的关系来看：兄妹&配偶数越多，生存的越少，猜测父母数/子女可能也是这样。

2.14 子女&父母数和生存的关系
2.15 按Cabin有无看获救情况
2.16 年龄和船票费用的关系
2.17 年龄和SibSp的关系
2.18 年龄和性别的关系

# 子女&父母数和生存的关系
S=data_train
S1=S.Survived
S2=S.Parch[S1==1].value_counts().sort_index()
S3=S.Parch[S1==0].value_counts().sort_index()
#print(S2)
#print(S3)
plt.bar(S2.index,S2,width=.4)
plt.bar(S3.index,-S3,width=.4)
plt.xticks(range(0,9))
ax=plt.gca()
ax.spines['bottom'].set_position(('data',0))
ax.spines['top'].set_color('none')
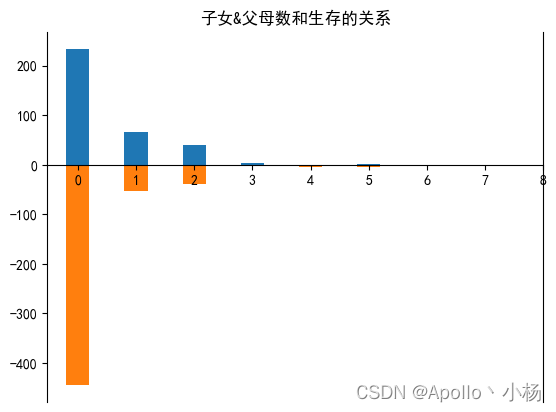
plt.title('子女&父母数和生存的关系')
plt.show()

在这里插入图片描述

# 按Cabin有无看获救情况
Survived_cabin = data_train.Survived[pd.notnull(data_train.Cabin)].value_counts()
Survived_nocabin = data_train.Survived[pd.isnull(data_train.Cabin)].value_counts()
df=pd.DataFrame({u'有':Survived_cabin, u'无':Survived_nocabin}).transpose()
df.plot(kind='bar', stacked=True)
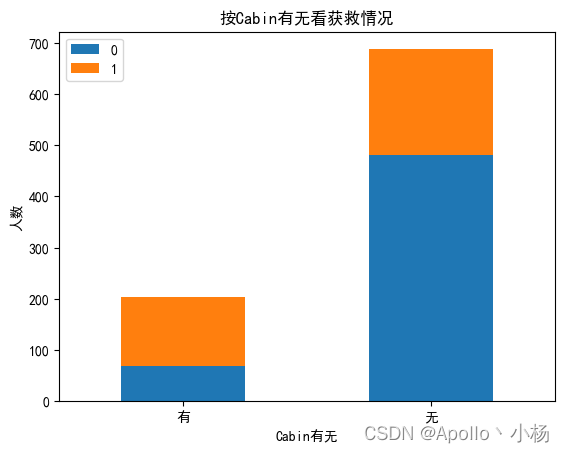
plt.title(u"按Cabin有无看获救情况")
plt.xticks(rotation=0)
plt.xlabel(u"Cabin有无") 
plt.ylabel(u"人数")
plt.show()

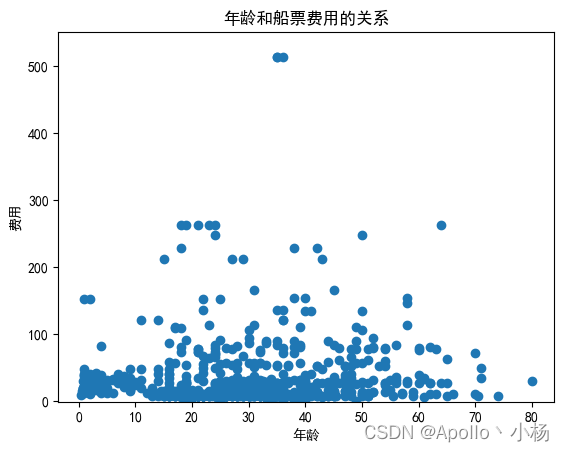
在这里插入图片描述

# 年龄和船票费用的关系
S=data_train.sort_values('Age')
S1=data_train.Age
S2=data_train.Fare
plt.scatter(S1,S2)
plt.xlabel(u'年龄')
plt.ylabel(u'费用')
plt.title(u"年龄和船票费用的关系")
plt.ylim(-1,550)
plt.show()

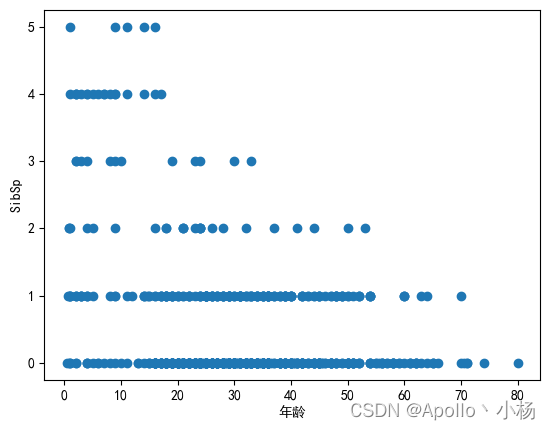
在这里插入图片描述

# 年龄和SibSp的关系
S=data_train.sort_values('Age')
S1=data_train.Age
S2=data_train.SibSp
plt.scatter(S1,S2)
plt.xlabel(u'年龄')
plt.ylabel(u'SibSp')
#plt.ylim(-1,550)
#plt.savefig(u'DF\年龄和SibSp的关系')
plt.show()

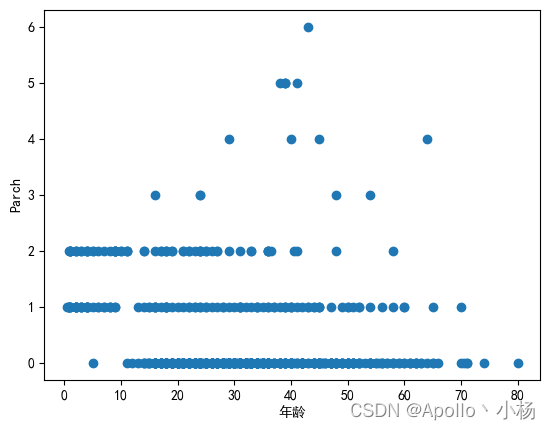
在这里插入图片描述

# 年龄和Parch的关系
S=data_train.sort_values('Age')
S1=data_train.Age
S2=data_train.Parch
plt.scatter(S1,S2)
plt.xlabel(u'年龄')
plt.ylabel(u'Parch')
plt.show()

在这里插入图片描述
从上述五个图中可以看出
a. 从子女&父母数和生存的关系来看：确实证明刚刚的猜想，父母数/子女人数越多，生存越少；
b. 从按Cabin有无看获救情况来看：缺失值有点多，按照图像的情况看无缺失值的更容易生存，所以预处理的时候按照是否有Cabin来处理；
c. 从年龄和船票费用的关系来看：好像没有太大关系，暂时不考虑；
d. 从年龄和SibSp的关系来看：两者还是有点关系的，可以作为年龄的特征；
e. 从年龄和Parch的关系来看：两者的关系不是很大，但可以作为年龄的备选特征。

第3步：补全缺失值
在第二步数据分析中，我们发现年龄Age主要和Pclass，Parch，SibSp有关，Fare、Sex可以作为备选特征，而Cabin则按照有和无来区分。
其中对于年龄采用随机森林分类回归来处理缺失值
(这一步是对训练集的缺失值的处理，测试集的处理则放到后面测试集的预处理中用df.to_csv()函数可以查看完成缺失值处理的数据集)

from sklearn.ensemble import RandomForestRegressor

def set_missing_ages(df):
    
    # 把选定特征取出来丢进Random Forest Regressor中
    age_df = df[['Age','Fare', 'Parch', 'SibSp', 'Pclass']]
    
    # 乘客分成已知年龄和未知年龄两部分
    known_age = age_df[age_df.Age.notnull()].values
   # print(known_age)
    unknown_age = age_df[age_df.Age.isnull()].values
    
    # y即目标年龄
    y = known_age[:, 0]
   # print(y)
    
    # X即特征属性值
    X = known_age[:, 1:]
   # print(X)
    
    # random_state表示一个种子的值，n_estimators表示子树的值，n_jobs表示最大的处理器，-1表示不限制
    rfr = RandomForestRegressor(random_state=0, n_estimators=2000, n_jobs=-1)
    # fit到RandomForestRegressor之中
    rfr.fit(X, y)
    
    # 用得到的模型进行未知年龄结果预测
    predictedAges = rfr.predict(unknown_age[:, 1:])
    
    # 用得到的预测结果填补原缺失数据
    df.loc[ (df.Age.isnull()), 'Age' ] = predictedAges 
    
    return df, rfr
    

def set_Cabin_type(df):
    df.loc[ (df.Cabin.notnull()), 'Cabin' ] = "Yes"
    df.loc[ (df.Cabin.isnull()), 'Cabin' ] = "No"
    return df

# 缺失值处理
data_train, rfr = set_missing_ages(data_train)
data_train = set_Cabin_type(data_train)

data_train.info()

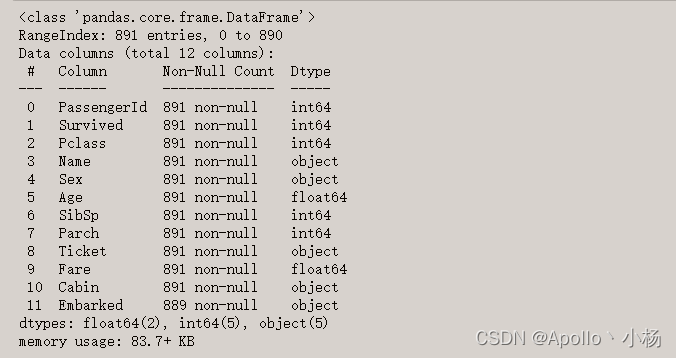
在这里插入图片描述
第4步：特征因子化
逻辑回归建模，需要输入的特征是数值型特征，所以需要对数据的特征因子化
特征因子化：以Cabin为例，原本一个属性维度，因为其取值可以是[‘yes’,‘no’]，而将其平展开为’Cabin_yes’,'Cabin_no’两个属性。
原本Cabin取值为yes的，在此处的"Cabin_yes"下取值为1，在"Cabin_no"下取值为0；
原本Cabin取值为no的，在此处的"Cabin_yes"下取值为0，在"Cabin_no"下取值为1。
特征因子化通过pd的get_dumies()函数来完成：

dummies_Cabin = pd.get_dummies(data_train['Cabin'], prefix= 'Cabin')
dummies_Embarked = pd.get_dummies(data_train['Embarked'], prefix= 'Embarked')
dummies_Sex = pd.get_dummies(data_train['Sex'], prefix= 'Sex')
dummies_Pclass = pd.get_dummies(data_train['Pclass'], prefix= 'Pclass')

# 合成数据集
df = pd.concat([data_train, dummies_Cabin, dummies_Embarked, dummies_Sex, dummies_Pclass], axis=1)
# 删除指定数据集，axis为0(index) or 1(columns),inpalace表示是否对内部操作，如果True则不返回
df.drop(['Pclass', 'Name', 'Sex', 'Ticket', 'Cabin', 'Embarked'], axis=1, inplace=True)

第5步：处理浮动较大的数值
逻辑回归建模中，浮动值极大的数字对收敛速度影响较大，所以要把Age和Fare进行scaling，也就是将他们特征化到[-1,1]之间。

# 处理数据集中浮动较大的数值到(-1,1)之间
import sklearn.preprocessing as preprocessing
scaler = preprocessing.StandardScaler()
# fit的数据需要以2维([[]])的形式传入
age_scale_param = scaler.fit(df[['Age']])
# 将fit的数据处理后的结果以np.array的形式返回
df['Age_scaled'] =age_scale_param.transform(df[['Age']])
fare_scale_param = scaler.fit(df[['Fare']])
df['Fare_scaled'] = fare_scale_param.transform(df[['Fare']])
df['Age']=df['Age_scaled']
df['Fare']=df['Fare_scaled']
df
# 最后得到的df数据情况如下所示
#df.to_csv('look.csv')

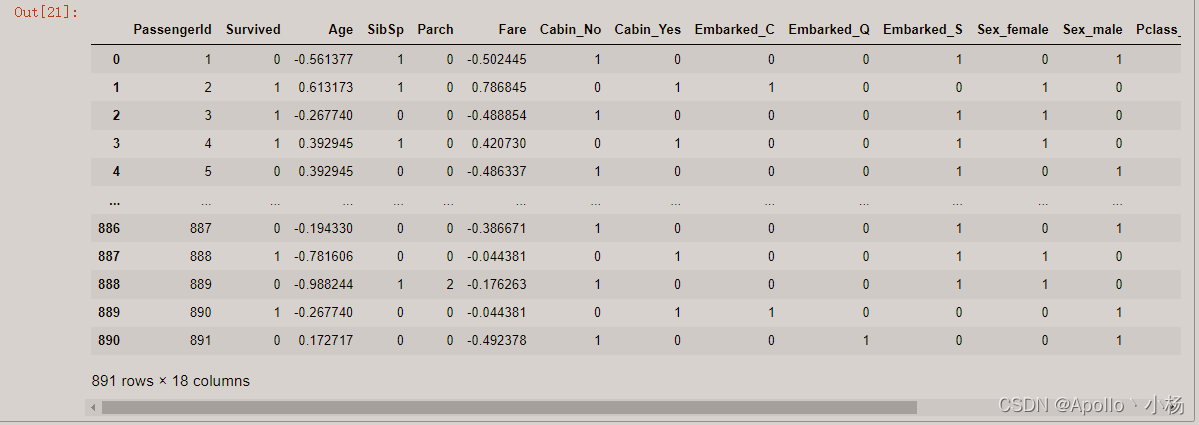
在这里插入图片描述
第6步：筛选数据

# 筛选数据(结果+特征)
# 利用正则表达式
train_df = df.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')
# train_df.to_csv('look_filter.csv')
train_np = train_df.values

第7步：数据建模

# y即Survival结果
y = train_np[:, 0]

# X即特征属性值
X = train_np[:, 1:]

from sklearn import linear_model
# fit到RandomForestRegressor之中
clf = linear_model.LogisticRegression(solver='liblinear',C=1.0, penalty='l1', tol=1e-6)
clf.fit(X, y)

在这里插入图片描述
第8步：测试集预处理

# 测试集预处理

data_test = pd.read_csv(r'test.csv')
 
# 缺失值处理
data_test.loc[ (data_test.Fare.isnull()), 'Fare' ] = 0
tmp_df = data_test[['Age','Fare', 'Parch', 'SibSp', 'Pclass']]
null_age = tmp_df[data_test.Age.isnull()].values
X = null_age[:, 1:]
predictedAges = rfr.predict(X)
data_test.loc[ (data_test.Age.isnull()), 'Age' ] = predictedAges

data_test = set_Cabin_type(data_test)

# 向量化
dummies_Cabin = pd.get_dummies(data_test['Cabin'], prefix= 'Cabin')
dummies_Embarked = pd.get_dummies(data_test['Embarked'], prefix= 'Embarked')
dummies_Sex = pd.get_dummies(data_test['Sex'], prefix= 'Sex')
dummies_Pclass = pd.get_dummies(data_test['Pclass'], prefix= 'Pclass')

# 合成新的数据集
df_test = pd.concat([data_test, dummies_Cabin, dummies_Embarked, dummies_Sex, dummies_Pclass], axis=1)
df_test.drop(['Pclass', 'Name', 'Sex', 'Ticket', 'Cabin', 'Embarked'], axis=1, inplace=True)

# 处理浮动值大的数据
age_scale_param = scaler.fit(df_test[['Age']])
df_test['Age_scaled'] =age_scale_param.transform(df_test[['Age']])
fare_scale_param = scaler.fit(df_test[['Fare']])
df_test['Fare_scaled'] = fare_scale_param.transform(df_test[['Fare']])
df_test['Age']=df_test['Age_scaled']
df_test['Fare']=df_test['Fare_scaled']

# 筛选数据(特征)
test = df_test.filter(regex='Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')
test = test.values
# test

第9步：结果预测

# 筛选数据(特征)
predictions = clf.predict(test)
result = pd.DataFrame({'PassengerId':data_test['PassengerId'].values, 'Survived':predictions.astype(np.int32)})
result.to_csv("reslut_1.csv", index=False)