算法介绍

Adam算法的发展经历了：SGD->SGDM->SGDNA->AdaGrad->AdaDelta->Adam->Adamax的过程。它是神经网络优化中的常用算法，在收敛速度上比较快，比SGD对收敛速度的纠结上有了很大的改进。但是该算法的学习率是不断减少的，可能收敛不到真正的最优解，实践中经常是前期Adam，后期SGD进行优化。
在这里插入图片描述

代码实现

现以如下无约束凸优化问题为例进行算法实施,
$\min 5x^2_1+2x^2_2+3x_1−10x_2+4$

# Adam之实现

import numpy
from matplotlib import pyplot as plt


# 目标函数0阶信息
def func(X):
    funcVal = 5 * X[0, 0] ** 2 + 2 * X[1, 0] ** 2 + 3 * X[0, 0] - 10 * X[1, 0] + 4
    return funcVal


# 目标函数1阶信息
def grad(X):
    grad_x1 = 10 * X[0, 0] + 3
    grad_x2 = 4 * X[1, 0] - 10
    gradVec = numpy.array([[grad_x1], [grad_x2]])
    return gradVec


# 定义迭代起点
def seed(n=2):
    seedVec = numpy.random.uniform(-100, 100, (n, 1))
    return seedVec


class Adam(object):

    def __init__(self, _func, _grad, _seed):
        '''
        _func: 待优化目标函数
        _grad: 待优化目标函数之梯度
        _seed: 迭代起始点
        '''
        self.__func = _func
        self.__grad = _grad
        self.__seed = _seed

        self.__xPath = list()
        self.__JPath = list()


    def get_solu(self, alpha=0.001, beta1=0.9, beta2=0.999, epsilon=1.e-8, zeta=1.e-6, maxIter=3000000):
        '''
        获取数值解,
        alpha: 步长参数
        beta1: 一阶矩指数衰减率
        beta2: 二阶矩指数衰减率
        epsilon: 足够小正数
        zeta: 收敛判据
        maxIter: 最大迭代次数
        '''
        self.__init_path()

        x = self.__init_x()
        JVal = self.__calc_JVal(x)
        self.__add_path(x, JVal)
        grad = self.__calc_grad(x)
        m, v = numpy.zeros(x.shape), numpy.zeros(x.shape)
        for k in range(1, maxIter + 1):
            # print("k: {:3d},   JVal: {}".format(k, JVal))
            if self.__converged1(grad, zeta):
                self.__print_MSG(x, JVal, k)
                return x, JVal, True

            m = beta1 * m + (1 - beta1) * grad
            v = beta2 * v + (1 - beta2) * grad * grad
            m_ = m / (1 - beta1 ** k)
            v_ = v / (1 - beta2 ** k)

            alpha_ = alpha / (numpy.sqrt(v_) + epsilon)
            d = -m_
            xNew = x + alpha_ * d
            JNew = self.__calc_JVal(xNew)
            self.__add_path(xNew, JNew)
            if self.__converged2(xNew - x, JNew - JVal, zeta ** 2):
                self.__print_MSG(xNew, JNew, k + 1)
                return xNew, JNew, True

            gNew = self.__calc_grad(xNew)
            x, JVal, grad = xNew, JNew, gNew
        else:
            if self.__converged1(grad, zeta):
                self.__print_MSG(x, JVal, maxIter)
                return x, JVal, True

        print("Adam not converged after {} steps!".format(maxIter))
        return x, JVal, False


    def get_path(self):
        return self.__xPath, self.__JPath


    def __converged1(self, grad, epsilon):
        if numpy.linalg.norm(grad, ord=numpy.inf) < epsilon:
            return True
        return False


    def __converged2(self, xDelta, JDelta, epsilon):
        val1 = numpy.linalg.norm(xDelta, ord=numpy.inf)
        val2 = numpy.abs(JDelta)
        if val1 < epsilon or val2 < epsilon:
            return True
        return False


    def __print_MSG(self, x, JVal, iterCnt):
        print("Iteration steps: {}".format(iterCnt))
        print("Solution:\n{}".format(x.flatten()))
        print("JVal: {}".format(JVal))


    def __calc_JVal(self, x):
        return self.__func(x)


    def __calc_grad(self, x):
        return self.__grad(x)


    def __init_x(self):
        return self.__seed


    def __init_path(self):
        self.__xPath.clear()
        self.__JPath.clear()


    def __add_path(self, x, JVal):
        self.__xPath.append(x)
        self.__JPath.append(JVal)


class AdamPlot(object):

    @staticmethod
    def plot_fig(adamObj):
        x, JVal, tab = adamObj.get_solu(0.1)
        xPath, JPath = adamObj.get_path()

        fig = plt.figure(figsize=(10, 4))
        ax1 = plt.subplot(1, 2, 1)
        ax2 = plt.subplot(1, 2, 2)

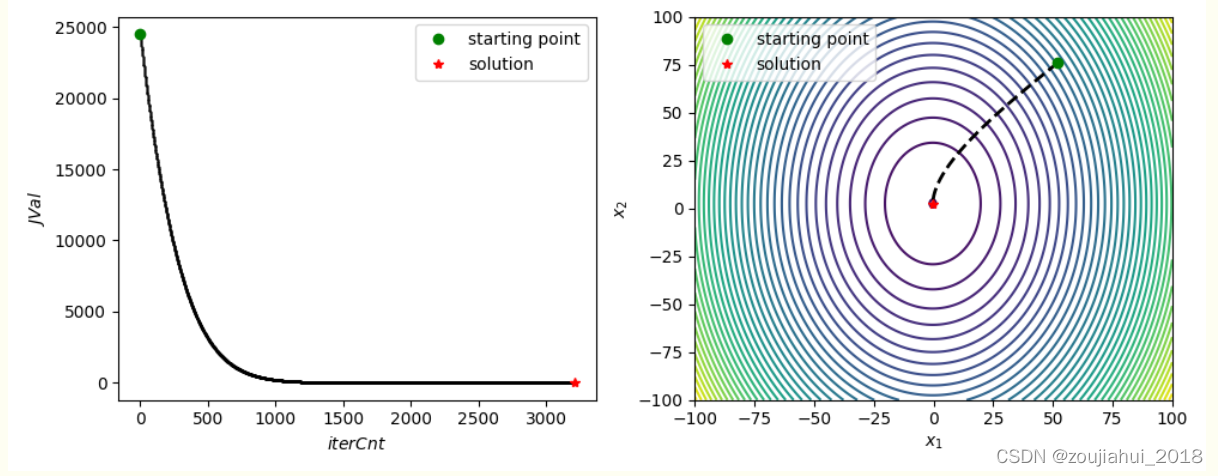
        ax1.plot(numpy.arange(len(JPath)), JPath, "k.", markersize=1)
        ax1.plot(0, JPath[0], "go", label="starting point")
        ax1.plot(len(JPath)-1, JPath[-1], "r*", label="solution")

        ax1.legend()
        ax1.set(xlabel="$iterCnt$", ylabel="$JVal$")

        x1 = numpy.linspace(-100, 100, 300)
        x2 = numpy.linspace(-100, 100, 300)
        x1, x2 = numpy.meshgrid(x1, x2)
        f = numpy.zeros(x1.shape)
        for i in range(x1.shape[0]):
            for j in range(x1.shape[1]):
                f[i, j] = func(numpy.array([[x1[i, j]], [x2[i, j]]]))
        ax2.contour(x1, x2, f, levels=36)
        x1Path = list(item[0] for item in xPath)
        x2Path = list(item[1] for item in xPath)
        ax2.plot(x1Path, x2Path, "k--", lw=2)
        ax2.plot(x1Path[0], x2Path[0], "go", label="starting point")
        ax2.plot(x1Path[-1], x2Path[-1], "r*", label="solution")
        ax2.set(xlabel="$x_1$", ylabel="$x_2$")
        ax2.legend()

        fig.tight_layout()
        # plt.show()
        fig.savefig("plot_fig.png")



if __name__ == "__main__":
    adamObj = Adam(func, grad, seed())

    AdamPlot.plot_fig(adamObj)