目录
一、栈
1.1 基本介绍
1.2 栈的思路分析
1.3 栈的代码实现
二、栈实现综合计算器
2.1 思路分析
2.2 代码实现(中缀表达式实现)
三、栈的前缀(波兰)、中缀、后缀(逆波兰)表达式
3.1 表达式的介绍
3.2 逆波兰计算器(后缀表达计算器)
3.2.1 思路分析
3.2.2 代码实现
3.3 中缀表达式转后缀表达式
3.3.1 思路分析
3.3.2 代码实现
一、栈
1.1 基本介绍
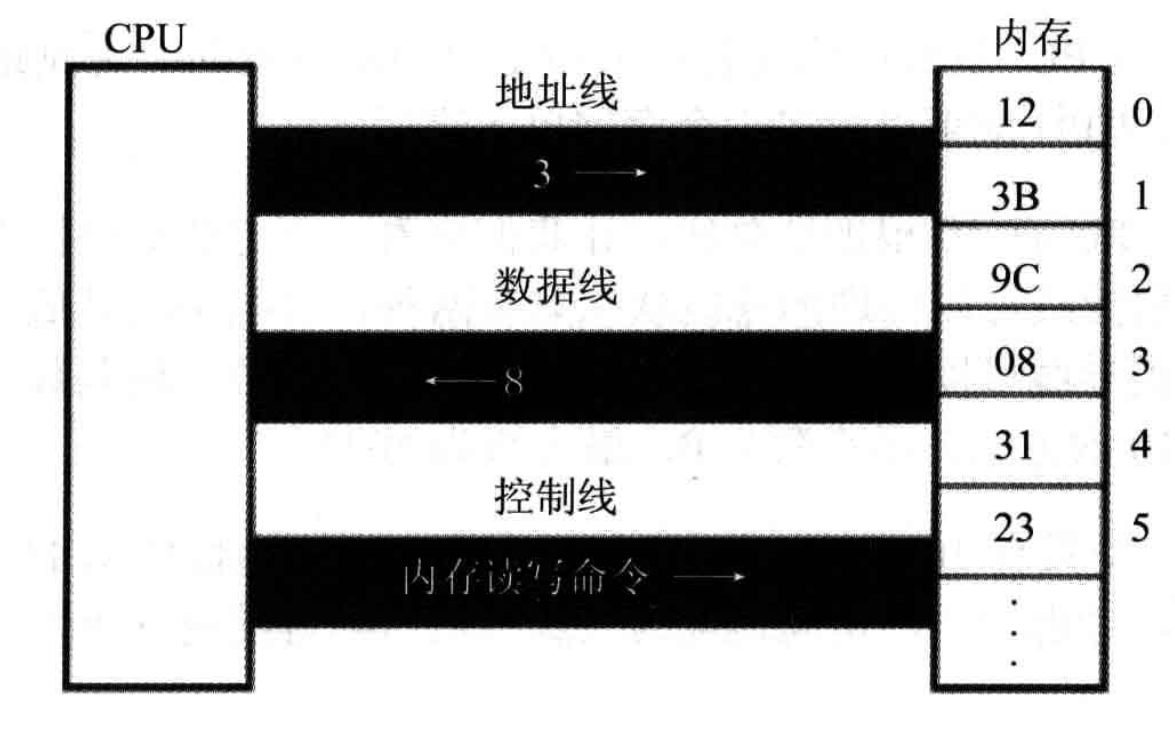
我们平时使用的计算器,其底层就是利用了栈这个概念对这个算式进行理解

- 栈的英文为(stack)
- 栈是一个先入后出(FILO-First In Last Out)的有序列表
- (stack)是限制表素的插入和除只能在性的同一端进行的一种性表。允许插入和删除的
- 端,为变化的一端,称为栈顶(Top),另一端为固定的一端,称为栈底(Bottom)
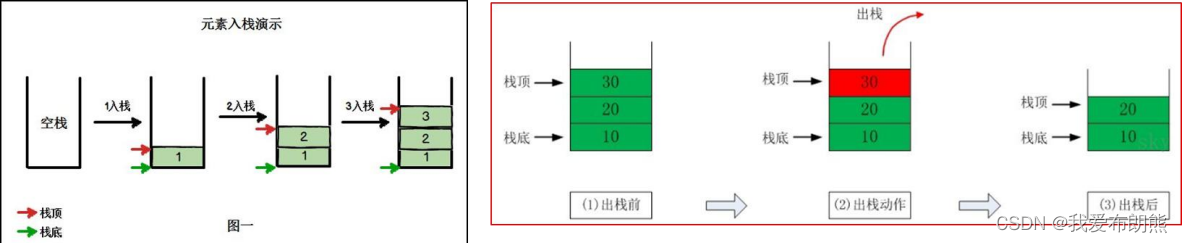
- 根据栈的定义可知,最先放入栈中元素在栈底,最后放入的元素在栈顶,而删除元素刚好相反,最后放入的元素最先删除,最先放入的元素最后删除
- 图解方式说明出栈(pop)和入栈(push)的概念
应用场景
- 子程序的调用:在跳往子程序前,会先将下个指令的地址存到堆栈中,直到子程序执行完后再将地址取出,以可到原来的程序中。
- 处理递归调用:和子程序的调用类似,只是除了储存下一个指令的地址外,也将参数、区域变量等数据存入堆栈中。
- 表达式的转换[中缀表达式转后缀表达式]与求值(实际解决)。又树的遍历
- 图形的深度优先(depth 一 first)搜索法
1.2 栈的思路分析
我们使用数组模拟栈的使用,由于栈是一种有序列表,那必然可以使用数组的结构来存储栈的数据内容。

1.3 栈的代码实现
// 定义一个ArrayStack 表示栈
class ArrayStack{
private int maxSize; //栈的大小
private int[] stack; //数组,用数组模拟栈,数据放在数组中
private int top = -1; //栈顶,初始化为-1
// 栈满
public boolean isFull(){
return top == maxSize-1;
}
// 栈空
public boolean isEmpty(){
return top ==-1;
}
// 入栈
public void push(int value){
if(isFull()){
// 栈满的话。不能进栈
System.out.println("栈满了,不能进栈");
return;
}
top++;
stack[top] =value;
}
// 出栈 栈顶数据返回
public int pop(){
// 看看是不是空
if(isEmpty()){
throw new RuntimeException("空了,没有数据");
}
// 有数据 先运行 再--
int value = stack[top];
top--;
return value;
}
// 遍历栈 从上往下遍历 只是展示并不出栈
public void list(){
if (isEmpty()){
System.out.println("栈空,没有数据");
}
for (int i =top; i>=0;i--){
System.out.println(stack[i]);
}
}
public ArrayStack(int maxSize) {
this.maxSize = maxSize;
stack = new int[this.maxSize];
}
}
二、栈实现综合计算器
2.1 思路分析
如果这个图看不明白我们直接分析一下就可以了。

我们分析一个3+2*6-2这个算式
① 首先创建一个数栈一个符号栈
② 我们使用index扫描我们的算式。当扫描到“3时”,“3”入栈的时候很显然是进入数栈,此时数栈中的指针指向“3”。
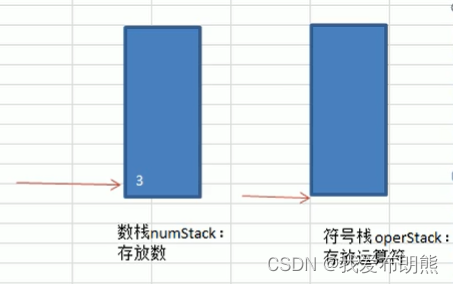
③ 然后index扫描到“+”号,入符号栈,因为前面没有符号可以比对,所以直接入栈,此时符号栈中的指针指向“+”
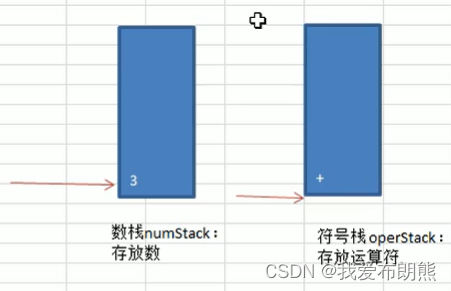
④ index扫描到“2”,入数栈,指针并且指向“2”
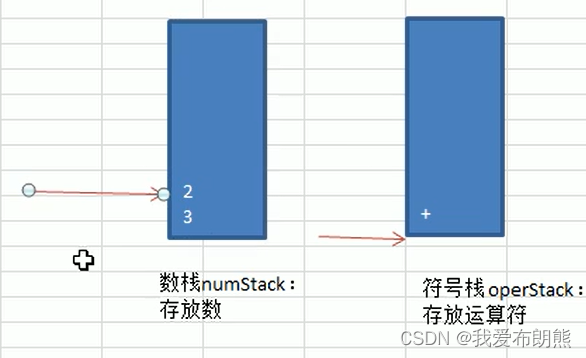
⑤ index扫描到“*”符号,由于“*”符号的运算级比我们栈中存在的“+”运算级要大,所以“*”直接入栈,并且指针指向“*”
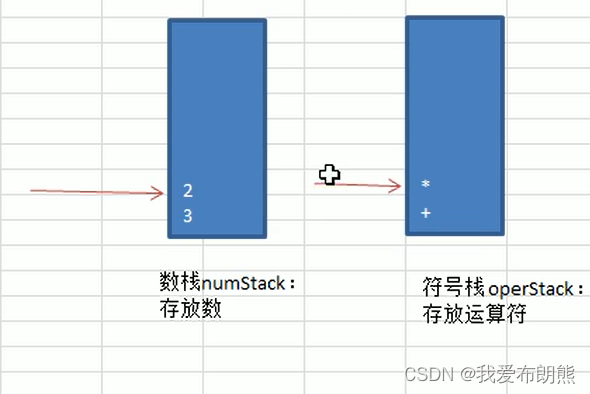
⑥ index扫描到“6”,入数栈,指针指向“6”
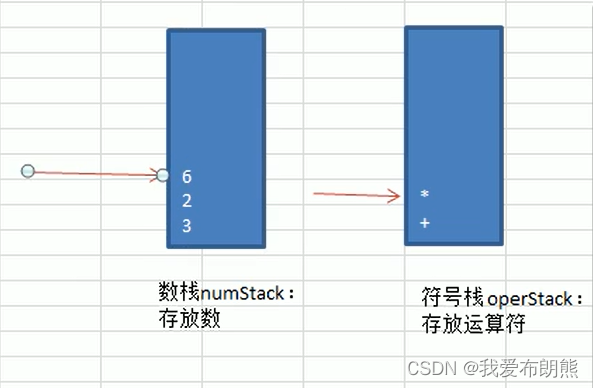
⑦ index扫描到“-”,然后这个地方很重要,由于“-”的运算级小于或者等于栈中的操作符(“*”),所以此时要从数栈中pop出两个数据(此时指针指向第二个pop出来的底下的一个位置),然后再从符号栈中pop出一个数据(此时指针移动到符号栈pop位置的底下的位置),进行运算。
但是!!!我们从数栈中pop出来的两个数的先后顺序会影响我们的结果,所以应该是pop2*pop1。让此时的操作结果入数栈(此时指针移动到此结果处)。我们刚刚扫描到的“-”入符号栈(此时指针移动到此符号处)
运算完成下图

⑧ index扫描到“2”,直接入数栈

⑨ 此时我们也扫描完毕了,我们按顺序从数栈和符号栈pop出相应的数和符号,并运行
数栈弹出两个,符号栈弹出一个。但是注意,符号栈弹出的两个数一定是有先后顺序的。
对于此题,当数栈弹出“2”,“12”时,指针应该是指向“3”,等“10”结果入栈后,再指向“10”
pop2(12)-pop1(2)=10 这样计算才对 ,此时10应该再入栈
当下面两个弹出的时候,数栈中没有东西了,然后计算出结果后,结果入栈,此时数据栈中只有一个元素,便是结果,并且符号栈中没有元素,全部弹出了
pop2(3)+pop1(10)=13
⑩ 最后数栈只有一个数字,便是表达式的结果
2.2 代码实现(中缀表达式实现)
public class Calculator {
public static void main(String[] args) {
// 完成表达式运算
String expression ="70-3-3";
// 创建两个栈,数栈和
ArrayStack numStack = new ArrayStack(10);
ArrayStack operStack = new ArrayStack(10);
// 定义扫描的相关变量 index
int index=0;
int num1=0;
int num2=0;
int oper=0;
int res=0;
char ch=' '; //每次扫描得到的char保存到ch中
String keepNum =""; //拼接多位数用的
// 开始循环扫描
while (true){
// 依次得到expression的每一个字符
// 截取字符串
ch = expression.substring(index,index+1).charAt(0);
// 判断是不是符号,如果是符号的话进入符号栈
if(operStack.isOper(ch)){
// 如果是运算符的话进入到这里
if(!operStack.isEmpty()){
// 如果符号栈不是空的话,就进行比较,如果当前的操作符的优先级小于或者等于栈中的优先级
// 就进行从数栈中pop两个,从符号栈pop一个运算,将算处的结果入栈,然后此时index指向的符号入栈
if(operStack.priority(ch) <= operStack.priority(operStack.peek())){
// 看看谁的优先级高,运行到这里说明我们的ch优先级小于等于符号栈顶部元素的优先级
// 从数栈中pop两个,从符号栈pop一个运算,将算处的结果入栈
num1 = numStack.pop();
num2 = numStack.pop();
oper = operStack.pop();
res = numStack.cal(num1,num2,oper);
// 运算结果入栈
numStack.push(res);
// 当前index指向的符号入栈
operStack.push(ch);
}else {
// 这种情况就是ch的运算符比,直接入栈
operStack.push(ch);
}
}else {
// 如果符号栈是空的话,直接放入符号栈
operStack.push(ch);
}
}else {
// 这种情况是ch是数字,直接放入符号栈
// numStack.push(ch); 这样写是错的 我们扫描的到数字其实不是数字,是字符,比如‘3’
// numStack.push(ch-48); 这样写只能算十以内的加减法
// 改进:我们不能发现一个数就入栈,因为可能会有多位数
// 处理多位数
keepNum +=ch;
// 如果ch已经是表达式的最后一位,直接入栈就行
if(index == expression.length()-1){
numStack.push( (Integer.parseInt(keepNum)));
}else {
// 判断下一个字符是不是数字,如果是数字的话就进行拼接
if (operStack.isOper( expression.substring(index+1,index+2).charAt(0) ) ){
// 这个时候后面是操作符,则入栈
numStack.push( (Integer.parseInt(keepNum)));
// 清空KeepNum
keepNum = "";
}
}
}
// index指针移动
index++;
// index是从0开始的
if(index >=expression.length()){
// 已经到最后了
break;
}
}
// 当表达式扫描完毕,按顺序从数栈和符号栈中取出元素计算
while (true){
// 如果符号栈是空,则计算到了最后一步
// 数栈中只有一个数字
if(operStack.isEmpty()){
break;
}
num1 = numStack.pop();
num2 = numStack.pop();
oper = operStack.pop();
res = numStack.cal(num1,num2,oper);
numStack.push(res);
}
System.out.println("结果:"+numStack.pop());
numStack.list();
operStack.list();
}
}
// 先创建一个栈
// 定义一个ArrayStack 表示栈
class ArrayStack {
private int maxSize; //栈的大小
private int[] stack; //数组,用数组模拟栈,数据放在数组中
private int top = -1; //栈顶,初始化为-1
public ArrayStack(int maxSize) {
this.maxSize = maxSize;
stack = new int[maxSize];
}
// 看栈顶元素,但不取出
public int peek(){
return stack[top];
}
// 栈满
public boolean isFull() {
return top == maxSize - 1;
}
// 栈空
public boolean isEmpty() {
return top == -1;
}
// 入栈
public void push(int value) {
if (isFull()) {
// 栈满的话。不能进栈
System.out.println("栈满了,不能进栈");
return;
}
top++;
stack[top] = value;
}
// 出栈 栈顶数据返回
public int pop() {
// 看看是不是空
if (isEmpty()) {
throw new RuntimeException("空了,没有数据");
}
// 有数据 先运行 再--
int value = stack[top];
top--;
return value;
}
// 遍历栈 从上往下遍历 只是展示并不出栈
public void list() {
if (isEmpty()) {
System.out.println("栈空,没有数据");
}
for (int i = top; i >= 0; i--) {
System.out.println(stack[i]);
}
}
//返回运算符的优先级,此优先级由程序员来确定:我们在此规定,数字越大,优先级越高
// char和int可以混用
public int priority(int oper){
// 假定表达式中只有下面四种符号
if(oper =='*' || oper == '/'){
return 1;
}else if(oper =='+' || oper =='-'){
return 0;
}else {
return -1;
}
}
// 判断是不是一个运算符
public boolean isOper(char var){
return var=='+' || var =='-' ||var=='*' || var=='/';
}
// 运算方法
public int cal(int num1,int num2 , int oper){
int res = 0; //res 用于存放计算的结果
switch (oper){
case '+':
res =num1+num2;
break;
case '-':
res = num2-num1;
break;
case '*':
res = num1*num2;
break;
case '/':
res = num2/num1;
break;
default:
break;
}
return res;
}
}

三、栈的前缀(波兰)、中缀、后缀(逆波兰)表达式
3.1 表达式的介绍
首先说明:不论是哪个表达式,一定要分清出栈的时候是pop1-pop2还是pop2-pop1
前缀表达式是pop1-pop2
后缀表达式是pop2-pop1 分清减数和被减数 在我们上面的二位数加减乘除代码中,也是pop2-pop1
描述
- 前缀表达式:波兰表达式,前缀表达式的运算符位于操作数之前
例如:(3+4)×5-6对应的前缀表达式就是 -×+3 4 5 6

- 中缀表达式:常见的运算表达式。我们小学学的就是中缀表达式
中缀表达式是我们最为熟悉的,但是对于计算机来说却很难操作,因此我们在计算结果的时候,往往会将中缀表达式转换成其他表达式来计算(一般转换成后缀表达式)
- 后缀表达式:逆波兰表达式,与前缀表达式相似,知识运算符位于操作数之后


3.2 逆波兰计算器(后缀表达计算器)
要求:支持小括号和多位整数,为了方便我们直接使用系统给我们的栈Stack
3.2.1 思路分析
我们刚刚看到的那个图就是我们的计算机求值思路

3.2.2 代码实现
public class PolandNotation {
public static void main(String[] args) {
// 先定义一个逆波兰表达式,为了方便数字和符号都是用空格间隔开
// (3+4)*5-6 后缀表达式就是下面
String suffixExpression ="3 4 + 5 × 6 -";
// 思路:
// 1.先将"3 4 + 5 × 6 -"放到ArrayList中
// 2.将ArrayList传递给一个方法,遍历ArrayList配合栈完成计算
List<String> rpnList = getListString(suffixExpression);
System.out.println(calculate(rpnList));
}
// 将一个逆波兰表达式,依次将数据和运算符放到ArrayList中
public static List<String> getListString (String suffixExpression){
// 分割
String[] split = suffixExpression.split(" ");
List<String> list = new ArrayList<>();
// 用这个api更快
Collections.addAll(list, split);
return list;
}
// 完成对逆波兰表达式的计算,我们已经变成了对List集合的遍历
public static int calculate(List<String> ls){
// 此时只需要一个栈就行了
Stack<String> stack = new Stack<>();
// 遍历ls
for (String item:ls){
if(item.matches("\\d+")){
// 入栈
stack.push(item);
}else {
// pop出两个数,并运算再入栈
int num1 = Integer.parseInt(stack.pop());
int num2 = Integer.parseInt(stack.pop());
int res=0;
if(item.equals("+")){
res = num1 + num2;
}else if(item.equals("-")){
res =num2-num1;
}else if(item.equals("×")){
res =num1*num2;
}else if(item.equals("/")){
res = num2/num1;
}else {
throw new RuntimeException("运算符有误");
}
// 结果入栈
stack.push(res+"");
}
}
// 最后留在stack中的数据是运算结果
return Integer.parseInt(stack.pop());
}
}

3.3 中缀表达式转后缀表达式
3.3.1 思路分析
小括号不是运算符,只是一个改变我们运算顺序的符号

3.3.2 代码实现
public class PolandNotation {
public static void main(String[] args) {
// 完成一个中缀表达式转成后缀表达式的功能
// 1+((2+3))×4-5 -----> 1 2 3 + 4 × + 5 -
// 我们对字符串操作不方便,将中缀表达式放入List集合找那个
String expression = "1+((2+3))×4-5";
// 转换成对应的list
List<String> InfixExpressionList =toInfixExpressionList(expression);
System.out.println("中缀表达式的List="+InfixExpressionList);
// 转换成后缀表达式的List
List<String> suffixExpressionList = parseSuffixExpressionList(InfixExpressionList);
System.out.println("后缀表达式的List"+suffixExpressionList);
System.out.println("结果:"+ calculate(suffixExpressionList));
}
// 将中缀表达式转成对应的List
public static List<String> toInfixExpressionList(String s){
// 定义List存放中缀表达式对应内容
List<String> ls = new ArrayList<>();
int i =0;
String str; //多位数拼接 因为计算的时候不可能光有一位数
char c; // 没遍历一个字符,就放入c中
do{
if( (c=s.charAt(i))<48 || (c=s.charAt(i))>57){
// 运行到这里肯定说明char不是0....9
ls.add(""+c);
i++;
}else {
// 这种情况就是数字了,但是我们需要考虑度多位数
// 保证是空串
str="";
while (i<s.length() && (c=s.charAt(i))>=48 && (c=s.charAt(i))<=57 ){
str +=c; //拼接
i++;
}
ls.add(str);
}
}while (i<s.length());
return ls;
}
// 中缀表达式转换成后缀表达式
public static List<String> parseSuffixExpressionList(List<String> ls){
// 定义两个栈
Stack<String> s1 = new Stack<>(); //符号栈
// 说明:我们s2栈只进栈,只有最后的时候倒序输出,所以我们选择List集合就可以了,方便
List<String> s2 =new ArrayList<>();//储存中间结果的栈
for(String item:ls){
// 如果是一个数就进栈s2
if(item.matches("\\d+")){
// 遇到操作数时,将其压s2;
s2.add(item);
}else if(item.equals("(")){
// 如果是左括号“(”,则直接压入s1
s1.push(item);
}else if(item.equals(")")){
// 如果是右括号“)”,则依次弹出s1栈顶的运算符,并压入s2,
// 直到遇到左括号为止,此时将这一对括号丢弃
while (!s1.peek().equals("(")){
s2.add(s1.pop());
}
// 将s1栈的左括号丢掉
s1.pop();
}else {
// 这种情况是匹配到字符的时候
// 优先级比栈顶运算符的高,也将运算符压入s1;
// 否则(运算符的优先级小于等于),将s1栈顶的运算符弹出并压入到s2中,再与s1中新的栈顶运算符相比较,如果遇到空栈或者(,直接进栈
while (s1.size() !=0 && Operation.getValue(s1.peek()) >= Operation.getValue(item)){
s2.add(s1.pop());
}
// 出循环的话,item的运算符肯定比顶部的高或者栈空了
// 优先级比栈顶运算符的高,也将运算符压入s1;
s1.push(item);
// if(s1.peek()==null || Operation.getValue(item)>Operation.getValue(s1.peek())){
// s1.push(item);
// }
}
}
// 将s1中剩余的运算符依次弹出并压入s2
while (s1.size()!=0){
s2.add(s1.pop());
}
// 因为是存放到列表里面,就不需要逆序输出了,现在已经是逆序表达式
return s2;
}
// 将一个逆波兰表达式,依次将数据和运算符放到ArrayList中
public static List<String> getListString (String suffixExpression){
// 分割
String[] split = suffixExpression.split(" ");
List<String> list = new ArrayList<>();
// 用这个api更快
Collections.addAll(list, split);
return list;
}
// 完成对逆波兰表达式的计算,我们已经变成了对List集合的遍历
public static int calculate(List<String> ls){
// 此时只需要一个栈就行了
Stack<String> stack = new Stack<>();
// 遍历ls
for (String item:ls){
if(item.matches("\\d+")){
// 入栈
stack.push(item);
}else {
// pop出两个数,并运算再入栈
int num1 = Integer.parseInt(stack.pop());
int num2 = Integer.parseInt(stack.pop());
int res=0;
if(item.equals("+")){
res = num1 + num2;
}else if(item.equals("-")){
res =num2-num1;
}else if(item.equals("×")){
res =num1*num2;
}else if(item.equals("/")){
res = num2/num1;
}else {
throw new RuntimeException("运算符有误");
}
// 结果入栈
stack.push(res+"");
}
}
// 最后留在stack中的数据是运算结果
return Integer.parseInt(stack.pop());
}
}
class Operation{
private static int ADD=1; //加
private static int SUB=1; //减
private static int MUL=2; //乘
private static int DIV=2; //除
// 写方法返回对应的优先级数字
public static int getValue(String operation){
operation= operation.trim();
int result =0;
switch (operation){
case "+":
result =ADD;
break;
case "-":
result = SUB;
break;
case "×":
result=MUL;
break;
case "/":
result =DIV;
break;
default:
System.out.println(operation);
System.out.println("不存在该运算符");
break;
}
return result;
}
}