树和二叉树
- 定义
- 二叉树
- 二叉树的物理结构
- 链式存储
- 数组
- 二叉树应用
- 查找
- 维持相对顺序
- 二叉树的遍历
- 深度优先遍历
- 前序遍历
- 中序遍历
- 后序遍历
- 二叉树广度优先遍历
- 层序遍历
定义
- 有且仅有一个特定的称为根的节点。
- 当n>1时,其余节点可分为m(m>0)个互不相交的有限集,每一个集合本身又是一个树,并称为根的子树。
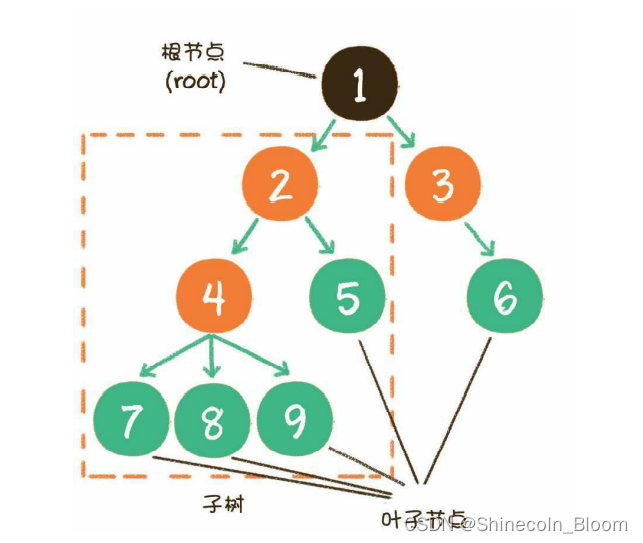
节点1是根节点(root);
节点5、6、7、8是树的末端,没有“孩子”,被称为叶子节点(leaf)。
图中的虚线部分,是根节点1的其中一个子树。
节点4的上一级节点,是节点4的父节点(parent);
从节点4衍生出来的节点,是节点4的孩子节点(child);
和节点4同级,由同一个父节点衍生出来的节点,是节点4的兄弟节点(sibling)。
树的最大层级数,被称为树的高度或深度。显然,上图这个树的高度是4。
二叉树
满二叉树:一个二叉树的所有非叶子节点都存在左右孩子,并且所有叶子节点都在同一层级上,那么这个树就是满二叉树。
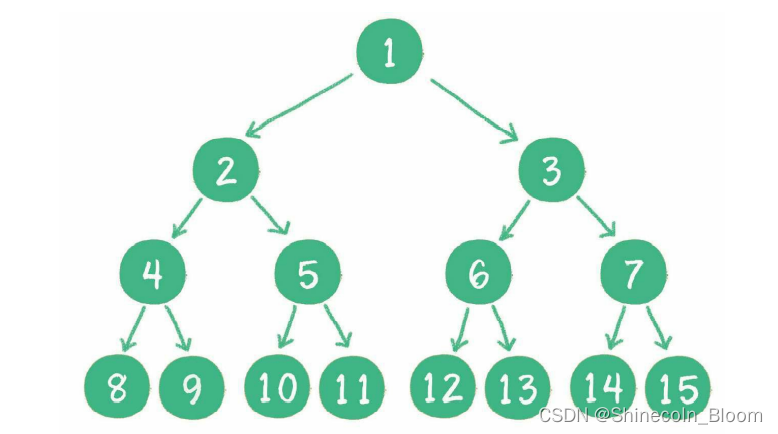
完全二叉树:对一个有n个节点的二叉树,按层级顺序编号,则所有节点的编号为从1到n。如
果这个树所有节点和同样深度的满二叉树的编号为从1到n的节点位置相同,则这个
二叉树为完全二叉树。

完全二叉树的条件没有满二叉树那么苛刻:
满二叉树要求所有分支都是满的;而完全二叉树只需保证最后一个节点之前的节点都齐全即可。
二叉树的物理结构
链式存储
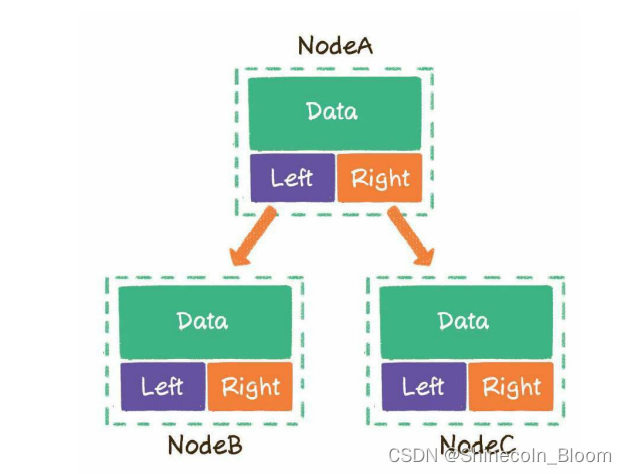
二叉树的每一个节点包含3部分。
- 存储数据的data变量
- 指向左孩子的left指针
- 指向右孩子的right指针
数组
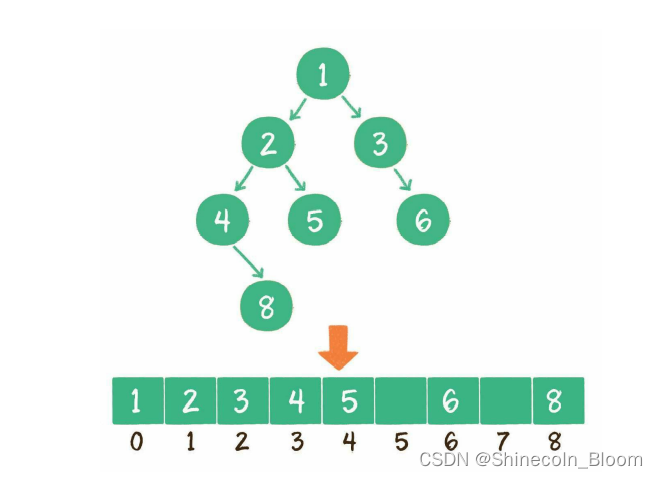
假设一个父节点的下标是parent,那么它的左孩子节点下标就是2×parent +1;右孩子节点下标就是2×parent + 2
反之
假设一个左孩子节点的下标是leftChild,那么它的父节点下标就是(leftChild-1)/ 2。
存在的问题:显然,对于一个稀疏的二叉树来说,用数组表示法是非常浪费空间的。
二叉堆:一种特殊的完全二叉树,就是用数组来存储的。
二叉树应用
查找
二叉查找树(二叉排序树)
如果左子树不为空,则左子树上所有节点的值均小于根节点的值
如果右子树不为空,则右子树上所有节点的值均大于根节点的值
左、右子树也都是二叉查找树
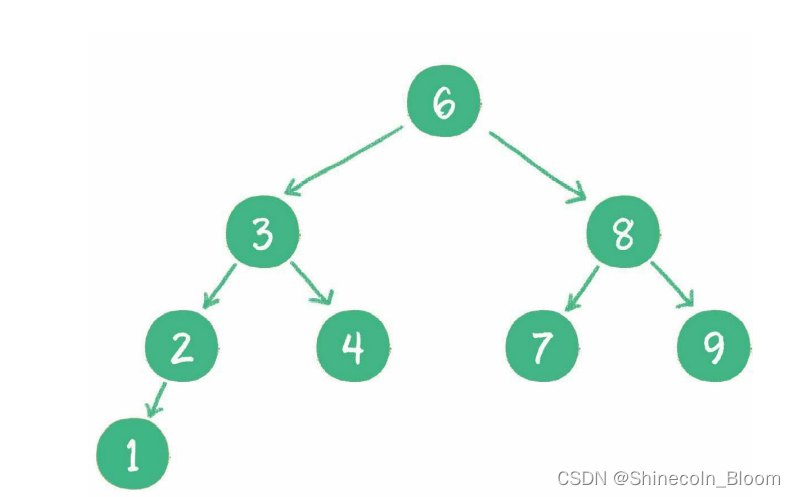
对于一个节点分布相对均衡的二叉查找树来说,如果节点总数是n,那么搜索节点的时间复杂度就是O(logn),和树的深度是一样的。
这种依靠比较大小来逐步查找的方式,和二分查找算法非常相似。
维持相对顺序
二叉查找树要求左子树小于父节点,右子树大于父节点,正是这样保证了二叉树的有序性。
一个问题:
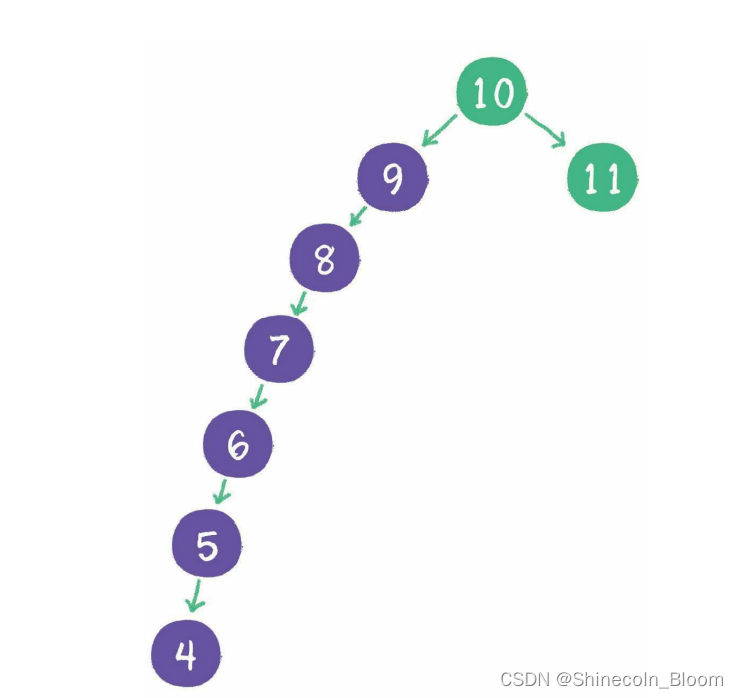
查询节点的时间复杂度也退化成了O(n)。
解决:就涉及二叉树的自平衡了。二叉树自平衡的方式有多种,如红黑树、AVL树、树堆等
二叉树的遍历
二叉树,是典型的非线性数据结构,遍历时需要把非线性关联的节点转化成一个线性的序列,以不同的方式来遍历,遍历出的序列顺序也不同。
从节点之间位置关系的角度
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
从更宏观的角度
- 深度优先遍历(前序遍历、中序遍历、后序遍历)。
- 广度优先遍历(层序遍历)。
深度优先遍历
前序遍历
输出顺序是根节点、左子树、右子树
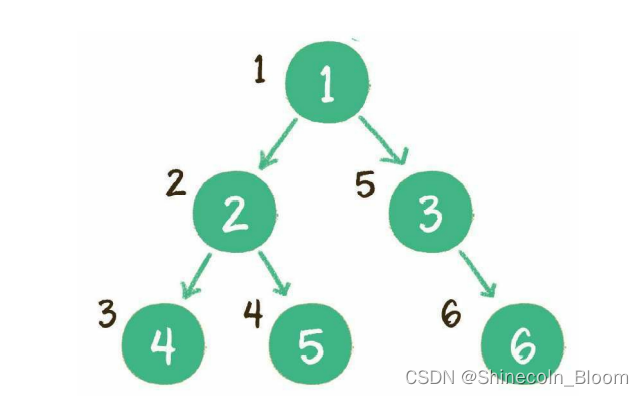
中序遍历
输出顺序是左子树、根节点、右子树。
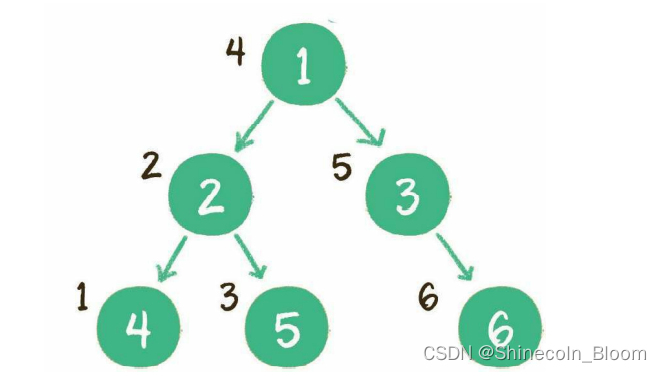
后序遍历
输出顺序是左子树、右子树、根节点。
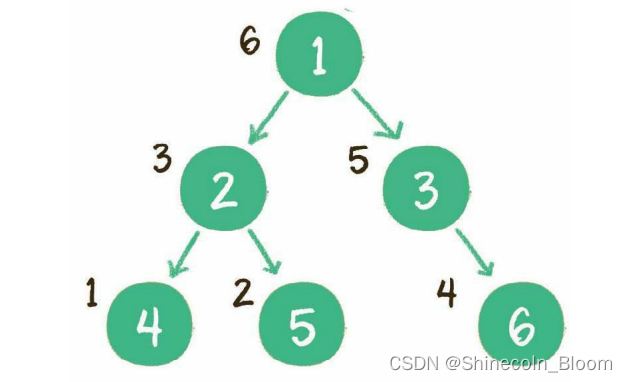
二叉树的这3种遍历方式,用递归的思路可以非常简单地实现出来
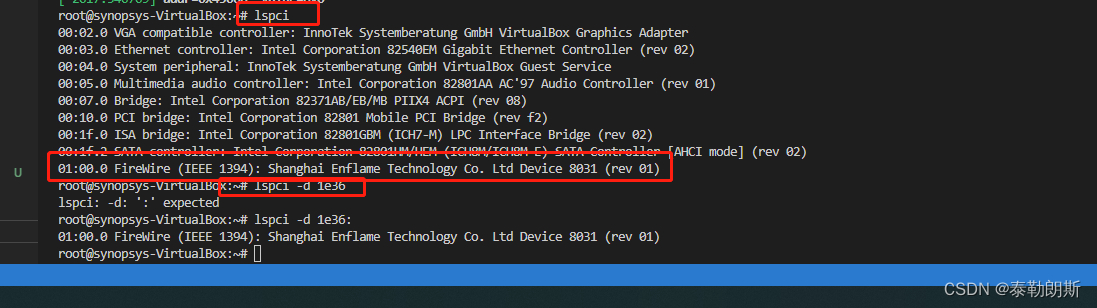
package dataStructure.binaryTree;
import java.util.Arrays;
import java.util.LinkedList;
public class bineryTree {
//静态内部类
//二叉树节点
private static class TreeNode{
int data;
TreeNode leftChild;
TreeNode rightChild;
public TreeNode(int data) {
this.data = data;
}
}
/**
* 前序遍历的链表节点的顺序.来创建二叉树
* @param inputList
* @return
*/
public static TreeNode precreatBinaryTree(LinkedList<Integer> inputList){
TreeNode node = null;
if(inputList==null||inputList.isEmpty()){
return null;
}
Integer data = inputList.removeFirst();
if(data!=null){
node = new TreeNode(data);
node.leftChild=precreatBinaryTree(inputList);
node.rightChild = precreatBinaryTree(inputList);
}
//将根节点返回(用于遍历,不返回根节点,这个树怎么找。。。。。)
return node;
}
/**
* 前序遍历
* @param node
*/
public static void preOrderTraveral(TreeNode node){
if(node==null){
return;
}
System.out.println(node.data);
preOrderTraveral(node.leftChild);
preOrderTraveral(node.rightChild);
}
/**
* 中序遍历
* @param node
*/
public static void inOrderTraveral(TreeNode node){
if (node==null){
return;
}
inOrderTraveral(node.leftChild);
System.out.println(node.data);
inOrderTraveral(node.rightChild);
}
/**
* 后序遍历
* @param node
*/
public static void postOrderTraveral(TreeNode node){
if (node==null){
return;
}
postOrderTraveral(node.leftChild);
postOrderTraveral(node.rightChild);
System.out.println(node.data);
}
public static void main(String[] args) {
//前序创建二叉树
LinkedList<Integer> inputList = new LinkedList<Integer>(Arrays.asList(new Integer[]{3,2,9,null,null,10,null,null,8,null,4}));
TreeNode treeNode = precreatBinaryTree(inputList);
System.out.println("前序遍历");
preOrderTraveral(treeNode);
System.out.println("中序遍历");
inOrderTraveral(treeNode);
System.out.println("后序遍历");
postOrderTraveral(treeNode);
}
}
二叉树的构建方法有很多,这里把一个线性的链表转化成非线性的二叉树,链表节点的顺序恰恰是二叉树前序遍历的顺序。链表中的空值,代表二叉树节点的左孩子或右孩子为空的情况。
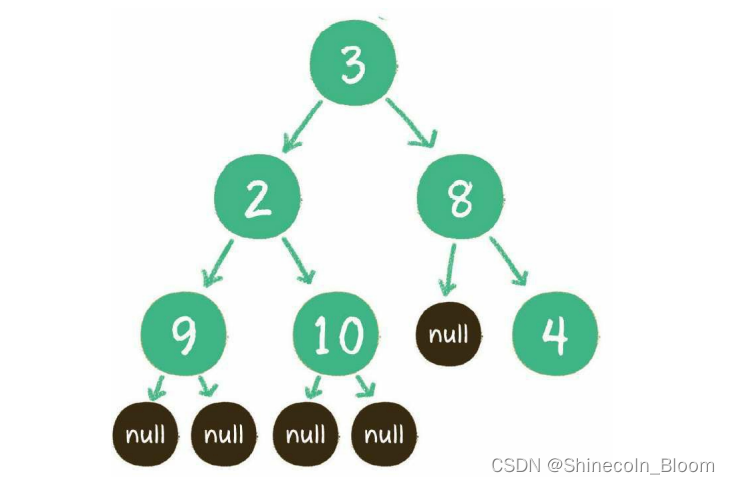
二叉树广度优先遍历
层序遍历
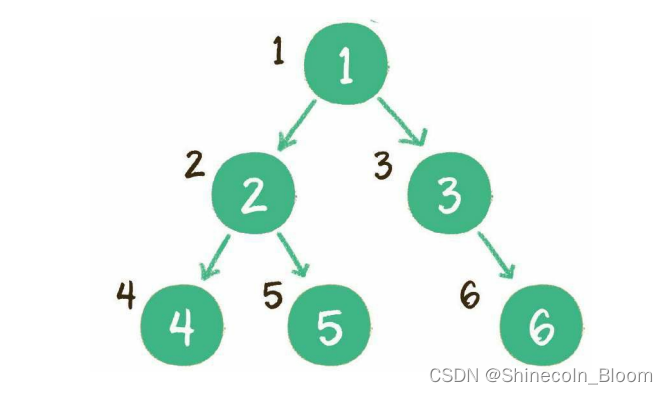
每个节点左侧的序号代表该节点的输出顺序。
借助队列完成二叉树层序遍历
//队列实现
public static void levelOrderTraversal(TreeNode root){
Queue<TreeNode> queue = new LinkedList<TreeNode>();
//向队列中插入元素,如果操作成功返回true,反之返回false。
queue.offer(root);
while (!queue.isEmpty()){
//poll()返回队首元素的同时删除队首元素
TreeNode node = queue.poll();
System.out.println(node.data);
if (node.leftChild!=null){
queue.offer(node.leftChild);
}
if(node.rightChild!=null){
queue.offer(node.rightChild);
}
}
}