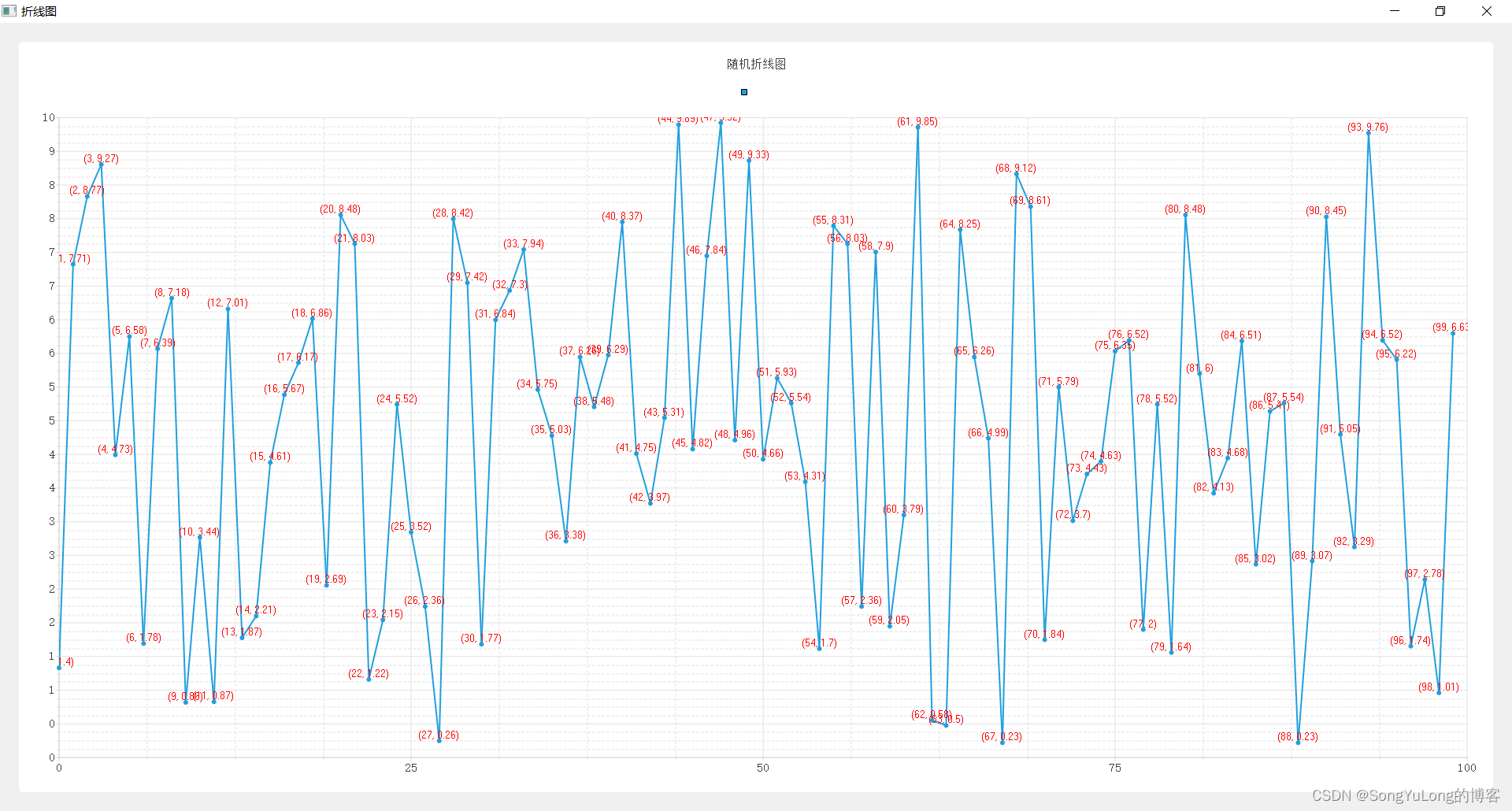
模型一：无限大导体平面

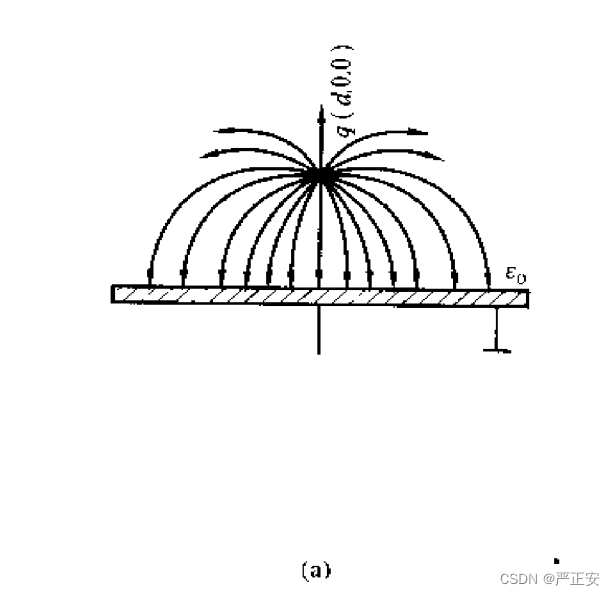
此处有几点理解需要格外谈一下

1. 只有在有电力线的地方，才会产生电场的作用

2.对于下平面的分析，下平面如果存在电荷的话，必然存在电力线，那么从无穷远处做功到此处，必然会存在电势，而表面接地，电势为0，两者相矛盾

3.对于镜像电荷的等效，我们可以用另一个角度来理解，类似于戴维南定理，我们如果想要简化上电场的分布，根据唯一性定理

上电场满足：

我们引入镜像电荷不改变方程的同时，也可以简化问题，这个就是镜像电荷的本质

---

模型二：球面镜像

情况一：球壳接地

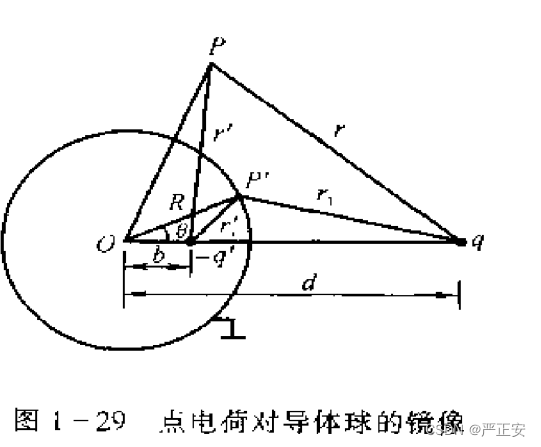
同样的几点思考： 

1. 关于球面镜像，思路还是类似的，因为导体球壳接地，所以内表面不可能存在电荷，有电荷就会有电场线，有电场线那么我们就可以做功，导出内表面的电势不为0

2. 同样外表面肯定会分布负电荷

我们根据余弦定理，可以解得这么一个结果，现在回想，其实这个就是一个类似阿氏圆的东西

---

 情况二：球壳不接地

那么根据电荷守恒，球壳内表面必然也会分布等量正电荷

此时就有一个疑问：

1. 既然一圈已经都有正电荷，肯定有电场线发出，在内部会是什么排布呢？

 因为电场线它本质上并不存在，先要存在电势差，才会有电场线，但是它电场线根本发不出来

2. 一个结论：

外表面电荷分布肯定是不均匀的，因为要维持等势面，所以不可能均匀

内表面电荷分布肯定是均匀的，因为要维持等势面，所以不可能不均匀

3. 关于电场线的抵消理解

关于电场线被外表面的电荷屏蔽，电场线被终结，他其实只是一个等效的理解，外部点电荷虽然被屏蔽，但也仅仅是在金属球里面被屏蔽，在外面依然发挥效果

4. 为什么内表面的电荷不被外表面的电荷给屏蔽掉？ 

有一个简单的想法，既然外表面可以屏蔽外部，那干脆顺带把内表面给屏蔽掉，这样在计算外部电势的时候，不是只要考虑外表面的点电荷吗？

 但是这个是不对的，因为内表面的电荷分布均匀，而外表面电荷分布不均匀，并且两者的总电荷量是守恒的，那么就意味着均匀对不均匀，外表面不可能可以屏蔽掉内表面

那又有新的疑问，为什么外表面电荷不能同时屏蔽两个电场呢？

这个可以理解为在导体内部，因为外表面电荷的产生原因就是屏蔽外部点电荷在内部电场中的作用，所以前后有因果

所以我们在计算外部的电场的时候，就不能想的太简单，简单的理解为球壳对外部电场没有作用

---

总而言之，我们现根据内部电场为0，确定内外电荷分布，然后再反求外部的场强分布

以上就是对于思路的理解

我们再从唯一性定理上来进行考虑，我们就是要放置电荷，首先根据表面电势为0，我们可以求出等效的感应电荷（本质就是在唯一性定理框架内的等效变形）

所以球壳不接地的时候，内部可以有两个镜像电荷来等效，原先的镜像电荷负责让球壳表面电势为0，再在中间放置镜像电荷提高球壳的电势，这样就可以使得外部的唯一性定理方程不变

---

球壳不接地，但是点电荷放置在内部

这个就是上一问反过来思考，只是这个时候，大家不禁会问，外界的点电荷该怎么放置呢？

我们点电荷无法放置进内部，但是放在外部的话，好像任何一个位置都无法拉高金属壳表面的电势？这一点我暂时还没有想明白

---

球壳可以接地，那势必也可以接其他电压，那么球壳表面电压达到接的电压的时候，那么相当于没接，如果没达到，那么电压会给电荷，让它达到，反之会吸收电压