一、为什么 Dijkstra 算法不适用于含负权的图

• 关于 Dijkstra 算法的讲解详见搜索与图论- Dijkstra 算法。

1. 理论推导

• Dijkstra 算法在运行过程中维持的关键信息是一组节点集合 S ，从源节点 S 到该集合中每个节点之间的最短路径已经被找到。算法重复从节点集合 V-S 中选择最短路径估计最小的节点 u ，将 u 加入到集合 S ，然后对所有从 u 出发的边进行操作。
• 当把一个节点选入集合 S 时，即意味着已经找到了从源点到这个点的最短路径，但若存在负权边，就与这个前提矛盾，可能会出现得出的距离加上负权后比已经得到 S 中的最短路径还短。（无法回溯）

2. 实例演示

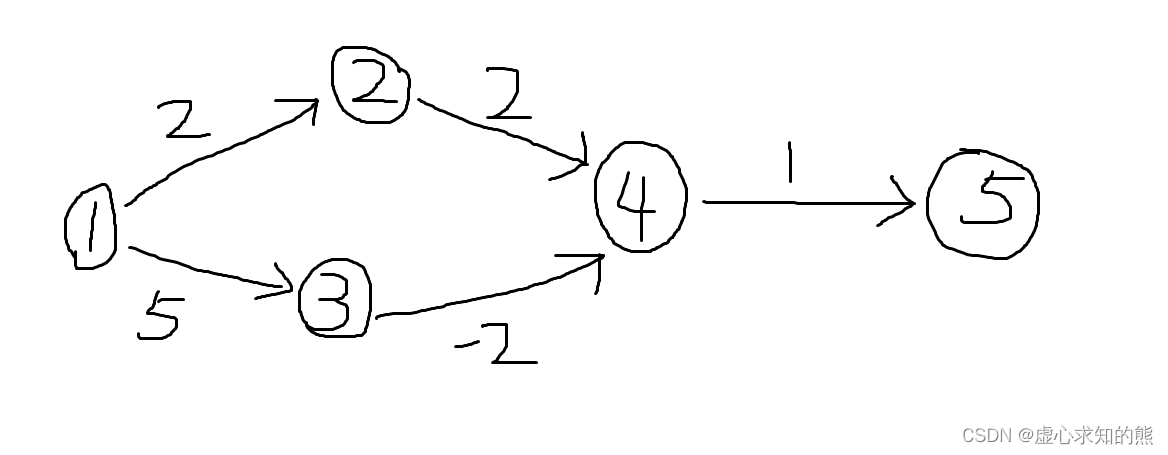
• 如下图为例，一共有 5 个点，也就说要循环 5 次，确定每个点的最短距离。
  

2.1 详细步骤

• （1） 初始 dist[1] = 0，1 号点距离起点 1 的距离为 0 。
• （2） 找到了未标识且离起点 1 最近的 1 号点，标记 1 号点，用 1 号点更新和它相连点的距离，2 号点被更新成 dist[2] = 2，3 号点被更新成 dist[3] = 5。
• （3） 找到了未标识且离起点 1 最近的 2 号点，标记 2 号点，用 2 号点更新和它相连点的距离，4 号点被更新成 dist[4] = 4。
• （4） 找到了未标识且离起点 1 最近的 4 号点，标记 4 号点，用 4 号点更新和它相连点的距离，5 号点被更新成 dist[5] = 5。
• （5） 找到了未标识且离起点 1 最近的 3 号点，标记 3 号点，用 3 号点更新和它相连点的距离，4 号点被更新成 dist[4] = 3。

2.2 结果

• 得到 Dijkstra 算法在图中走出来的最短路径是1 -> 2 -> 4 -> 5，算出 1 号点到 5 号点的最短距离是 2 + 2 + 1 = 5，然而还存在一条路径是1 -> 3 -> 4 -> 5，该路径的长度是5 + (-2) + 1 = 4。
• 因此，Dijkstra 算法失效。
• 我们可以发现如果有负权边的话 4 号点经过标记后还可以继续更新，但此时 4 号点已经被标记过了，所以 4 号点不能被更新了，只能一条路走到黑。
• 当用负权边更新 4 号点后 5 号点距离起点的距离我们可以发现可以进一步缩小成 4。
• 总结：Dijkstra 不能解决负权边是因为 Dijkstra要求每个点被确定后，dist[j] 就是最短距离了，之后就不能再被更新了（一锤子买卖），而如果有负权边的话，那已经确定的点的 dist[j] 不一定是最短了，可能还可以通过负权边进行更新。

二、bellman-ford 算法

• 针对负权边的问题，我们采用 bellman-ford 算法进行解决。

1. 简介

• 贝尔曼-福特算法（Bellman-Ford）是由理查德·贝尔曼（Richard Bellman）和莱斯特·福特创立的，求解单源最短路径问题的一种算法。其优于 Dijkstra 算法的方面是边的权值可以为负数、实现简单，缺点是时间复杂度过高。但它也有特别的用处，一般用于实现通过 m 次迭代求出从起点到终点不超过 m 条边构成的最短路径。

2. 基本思路

• bellman-ford 算法的思路也很简单，直接就是两层循环，内层循环所有边，外层循环就是循环所有边的次数，这个外层循环次数一般是题目控制的。时间复杂度是 O(n*m)。
• 首先n次迭代，每一次循环所有边。这里用 a，b，w 表示存在一条从 a 走到 b 的边，权重是 w。
• 这里存边方式有很多种，可以用邻接表，结构体等。遍历所有边的时候更新一下其他点的距离，和 Dijkstra 算法类似，用当前这个点更新和它相连的点距离起点的距离。
• 这里使用 dist 数组表示每个点到起点的距离，那么更新操作就是 dist[b]=min(dist[b],dist[a]+w) ，这样就可以更新和 a 相连的 b 点距离起点的距离，这个更新的过程就是”松弛操作”。
• 在循环所有边的时候，每一次循环要先把 dist 数组备份一下。

3. 简单举例

• 如下图例子，红色边表示权重，求一下 1 号点到 5 号点的最短路径。
  
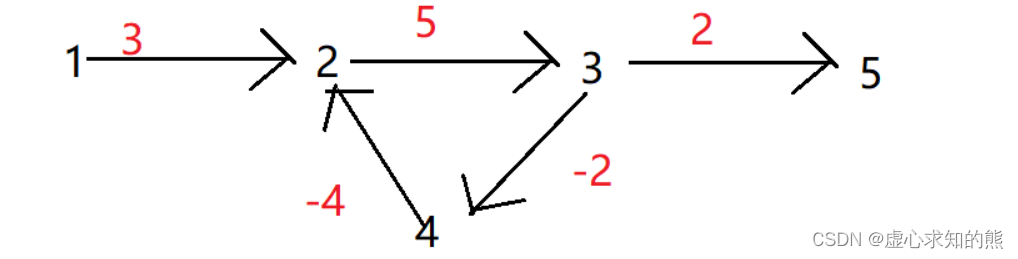
• 从 1 号点走到 2 号点，2，3，4 号点围成了一个圈，圈的总权重是 5 + (-4) + (-2) = (-1)，那么转一圈长度就会减一，因此我们可以转无穷多圈，转无穷多圈总长度就会变成负无穷，出圈的话还是负无穷。
• 所以说图中存在负权回路的话，从 1 号点到 n 号点的距离就会变成负无穷，就不存在了。
• bellman-ford 算法是可以判断图中存不存在负权回路。
• 首先上面的迭代次数是有实际意义的，比如我们迭代了 k 次，那么我们求的最短距离就是从 1 号点经过不超过 k 条边走到 n 号点的最短距离。所以在第 n 次迭代的时候又更新了某些边的话，就说明路径中一定存在环，并且是负权回路。因为第 n 次迭代在不存在负权回路的情况下是遍历到第 n 号点了，后面是没有点了，如果还能更新，说明路径中存在回路，而且是负权回路。

4. bellman-ford 算法具体实现过程详见例题有边数限制的最短路。

三、bellman-ford 算法例题——有边数限制的最短路

题目描述

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环， 边权可能为负数。
请你求出从 1 号点到 n 号点的最多经过 k 条边的最短距离，如果无法从 1 号点走到 n 号点，输出impossible 。

输入格式

第一行包含三个整数 n，m，k。
接下来 m 行，每行包含三个整数 x，y，z，表示存在一条从点 x 到点 y 的有向边，边长为 z。
点的编号为 1∼n。

输出格式

输出一个整数，表示从 1 号点到 n 号点的最多经过 k 条边的最短距离。
如果不存在满足条件的路径，则输出 impossible 。

数据范围

1 ≤ n，k ≤ 500
1 ≤ m ≤ 10000
1 ≤ x，y ≤ n
任意边长的绝对值不超过 10000。

输入样例

3 3 1
1 2 1
2 3 1
1 3 3

输出样例

3

具体实现

1. 样例演示

• 首先，输入 n=3，m=3，k=1；表示从 1 号点到 3 号点最多经过 1 条边的最短距离。下面共有 3 条边。
• 第一条边是从 1 号点到 2 号点，边长为 1。
• 第二条边是从 2 号点到 3 号点，边长为 1。
• 第三条边是从 1 号点到 3 号点，边长为 3。
• 具体情况如下图所示：
  
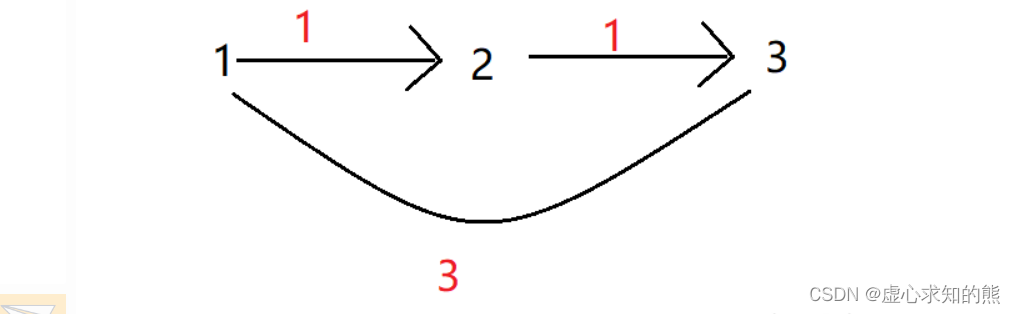
• 要求从 1 号点出发到 3 号点最多经过 1 条边的最短距离，通过图很容易就可以看出，最短距离就是 3，也就是 1 号点直接到 3 号点的距离。
• 因此，输出为 3。

2. 实现思路

• 由 bellman-ford 算法的步骤，也就是两层循环，外层循环题目控制的是 k，也就是 1，内层循环所有的边。也就说只会进行一次迭代。
• 看一下内层循环的过程，首先一共有三条边，所以内层循环要循环三次。我们看一下内层循环后的结果。注意：这里是没有备份 dist 数组的结果。

	1号点	2号点	3号点
内层循环第一次执行	0	∞	∞
内层循环第二次执行	0	1	∞
内层循环第三次执行	0	1	2

• 由上表可得，如果没有备份 dist 数组的话，最短距离就变成了 2。内层循环只迭代了一次，但是在更新的过程中会发生”串联”。比如说先更新 2 号点，然后用 2 号点更新 3 号点距离起点的距离，这样就发生了”串联”，3 号点不能被 2 号点更新，这样就不满足题目要求了，因为题目要求最多不经过 1 条边。
• 为了解决“串联”问题的发生，保证更新的时候只用上一次循环的结果就行，所以先备份一下。
• 备份之后 last 数组存的就是上一次循环的结果，用上一次循环的结果来更新距离。
• 所以写成 dist[b]=min(dist[b],last[a]+w) 来更新距离。

3. 代码注解

• int back[N]；备份数组防止串联。
• memset(dist,0x3f,sizeof dist)；初始化距离。
• memcpy(last, dist, sizeof dist)；将 dist 数组的内容复制到 last 数组当中，数据类型为 dist 的数据类型。
• dist[n] > 0x3f3f3f3f / 2；是因为在图当中，可能会存在负权边，假设 5 号点到 n 号点的距离为 -2，5 号点是 0x3f3f3f3f，n 号点也是 0x3f3f3f3f，就有可能将 n 号点给更新为 0x3f3f3f3f-2，在数据量较小的情况下没有影响。
• 其他代码注解标识在实现代码当中。

4. 实现代码

#include <bits/stdc++.h>
using namespace std;

const int N = 510, M = 10010;


//使用结构体存储边的信息
struct Edge
{
    int a, b, c;
}edges[M];

int n, m, k;
int dist[N];
int last[N];

void bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);

    dist[1] = 0;
    for (int i = 0; i < k; i ++ )
    {
        memcpy(last, dist, sizeof dist);
        //更新所有的边
        for (int j = 0; j < m; j ++ )
        {
            auto e = edges[j];
            //使用backup:避免给a更新后立马更新b, 这样b一次性最短路径就多了两条边出来
            dist[e.b] = min(dist[e.b], last[e.a] + e.c);
        }
    }
}

int main()
{
    cin >> n >> m >> k;

    for (int i = 0; i < m; i ++ )
    {
        int a, b, c;
        cin >> a >> b >> c;
        edges[i] = {a, b, c};
    }

    bellman_ford();

    if (dist[n] > 0x3f3f3f3f / 2)
    {
        puts("impossible");
    }
    else 
    {
        cout << dist[n] << endl;
    }
    system("pause");
    return 0;
}