---

什么是树

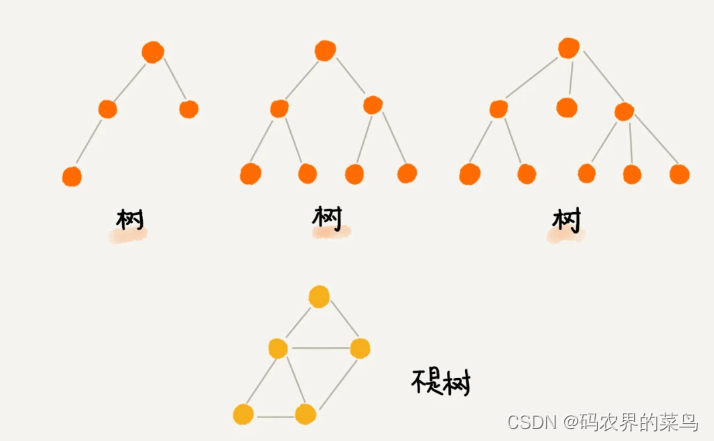
“树”这种数据结构真的很像我们现实生活中的“树”，这里面每个元素我们叫做“节点”；用来连接相邻节点之间的关系，我们叫做“父子关系”。

比如下面这幅图，A 节点就是 B 节点的父节点，B 节点是 A 节点的子节点。B、C、D 这三个节点的父节点是同一个节点，所以它们之间互称为兄弟节点。我们把没有父节点的节点叫做根节点，也就是图中的节点 E。我们把没有子节点的节点叫做叶子节点或者叶节点，比如图中的 G、H、I、J、K、L 都是叶子节点。

除此之外，关于“树”，还有三个比较相似的概念：高度（Height）、深度（Depth）、层（Level）。它们的定义是这样的：

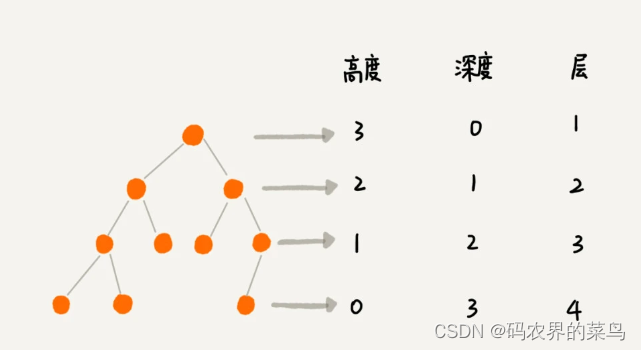
• “高度”这个概念，其实就是从下往上度量，比如我们要度量第 10 层楼的高度、第 13 层楼的高度，起点都是地面。所以，树这种数据结构的高度也是一样，从最底层开始计数，并且计数的起点是 0。
• “深度”这个概念在生活中是从上往下度量的，比如水中鱼的深度，是从水平面开始度量的。所以，树这种数据结构的深度也是类似的，从根结点开始度量，并且计数起点也是 0。
• “层数”跟深度的计算类似，不过，计数起点是 1，也就是说根节点位于第 1 层。

什么是二叉树

二叉树，顾名思义，每个节点最多有两个“叉”，也就是两个子节点，分别是左子节点和右子节点。不过，二叉树并不要求每个节点都有两个子节点，有的节点只有左子节点，有的节点只有右子节点。

如何表示（或者存储）一棵二叉树

想要存储一棵二叉树，我们有两种方法，一种是基于指针或者引用的二叉链式存储法，一种是基于数组的顺序存储法。

链式存储法

我们先来看比较简单、直观的链式存储法。从图中你应该可以很清楚地看到，每个节点有三个字段，其中一个存储数据，另外两个是指向左右子节点的指针。我们只要拎住根节点，就可以通过左右子节点的指针，把整棵树都串起来。这种存储方式我们比较常用。大部分二叉树代码都是通过这种结构来实现的。

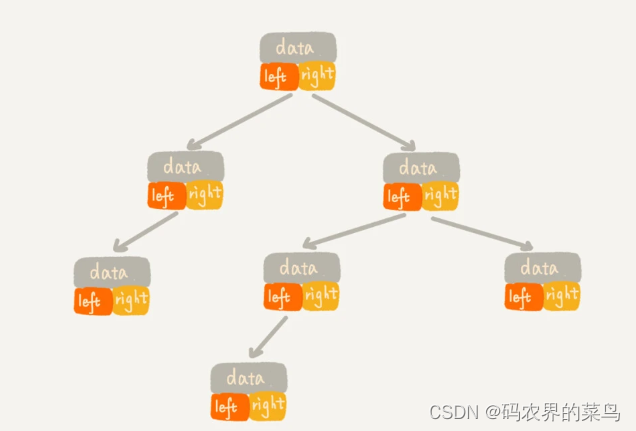
顺序存储法

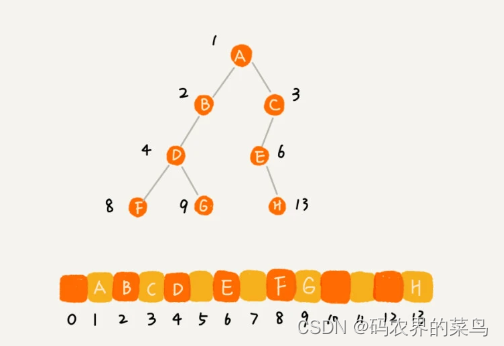
我们把根节点存储在下标 i = 1 的位置，那左子节点存储在下标 2 * i = 2 的位置，右子节点存储在 2 * i + 1 = 3 的位置。以此类推，B 节点的左子节点存储在 2 * i = 2 * 2 = 4 的位置，右子节点存储在 2 * i + 1 = 2 * 2 + 1 = 5 的位置。

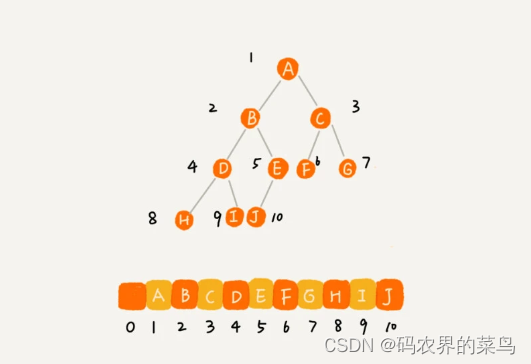
如果节点 X 存储在数组中下标为 i 的位置，下标为 2 * i 的位置存储的就是左子节点，下标为 2 * i + 1 的位置存储的就是右子节点。反过来，下标为 i/2 的位置存储就是它的父节点。通过这种方式，我们只要知道根节点存储的位置（一般情况下，为了方便计算子节点，根节点会存储在下标为 1 的位置），这样就可以通过下标计算，把整棵树都串起来。

二叉树的分类

二叉树的分类，我们通过下面这个图来看下：

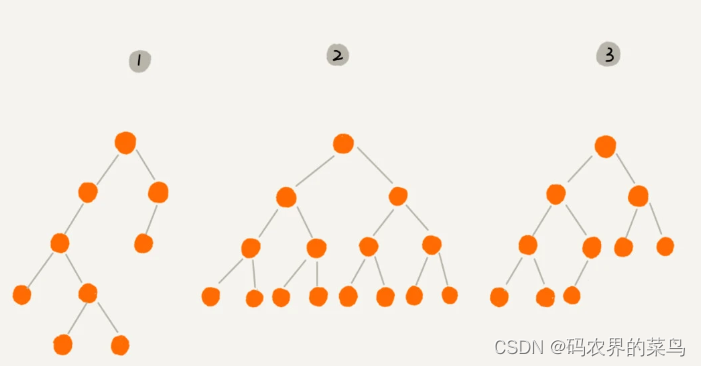
这个图里面，有两个比较特殊的二叉树，分别是编号 2 和编号 3 这两个。

其中，编号 2 的二叉树中，叶子节点全都在最底层，除了叶子节点之外，每个节点都有左右两个子节点，这种二叉树就叫做满二叉树。

编号 3 的二叉树中，叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大，这种二叉树叫做完全二叉树。

满二叉树很好理解，也很好识别，但是完全二叉树，有的人可能就分不清了。我画了几个完全二叉树和非完全二叉树的例子，你可以对比着看看。

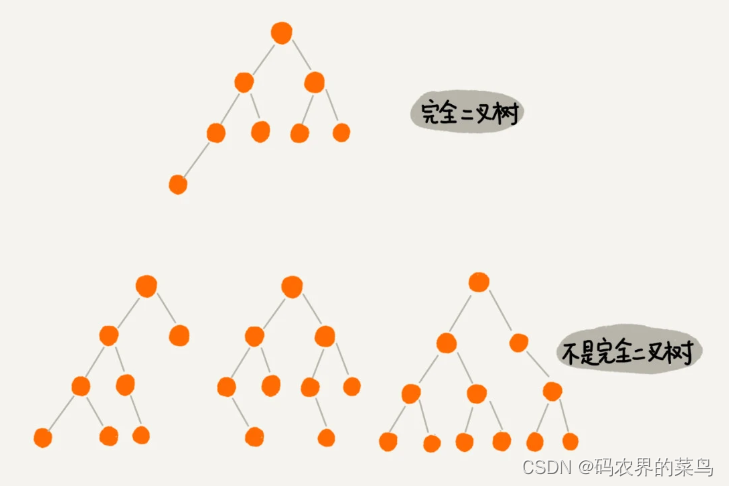
你可能会说，满二叉树的特征非常明显，我们把它单独拎出来讲，这个可以理解。但是完全二叉树的特征不怎么明显啊，单从长相上来看，完全二叉树并没有特别特殊的地方啊，更像是“芸芸众树”中的一种。

其实，当我们用数组来存储一个树的时候，完全二叉树的特别点就能体现出来了，比如上面我们用数组表示的那个图示中，其实就是一个完全二叉树，所以仅仅“浪费”了一个下标为 0 的存储位置。如果是非完全二叉树，其实会浪费比较多的数组存储空间。你可以看我举的下面这个例子：

所以，如果某棵二叉树是一棵完全二叉树，那用数组存储无疑是最节省内存的一种方式。因为数组的存储方式并不需要像链式存储法那样，要存储额外的左右子节点的指针。这也是为什么完全二叉树会单独拎出来的原因，也是为什么完全二叉树要求最后一层的子节点都靠左的原因。

二叉树的遍历

经典的方法有三种，前序遍历、中序遍历和后序遍历。其中，前、中、后序，表示的是节点与它的左右子树节点遍历打印的先后顺序。

• 前序遍历是指，对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。
• 中序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树。
• 后序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身。
  
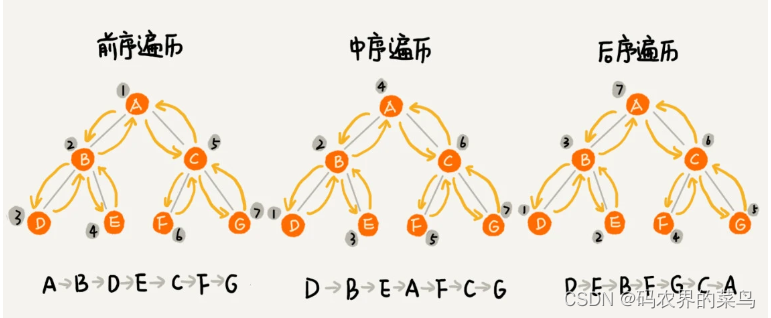
  实际上，二叉树的前、中、后序遍历就是一个递归的过程。比如，前序遍历，其实就是先打印根节点，然后再递归地打印左子树，最后递归地打印右子树。

二叉查找树

二叉查找树是二叉树中最常用的一种类型，也叫二叉搜索树。顾名思义，二叉查找树是为了实现快速查找而生的。不过，它不仅仅支持快速查找一个数据，还支持快速插入、删除一个数据。它是怎么做到这些的呢？

这些都依赖于二叉查找树的特殊结构。二叉查找树要求，在树中的任意一个节点，其左子树中的每个节点的值，都要小于这个节点的值，而右子树节点的值都大于这个节点的值。 我画了几个二叉查找树的例子，你一看应该就清楚了。

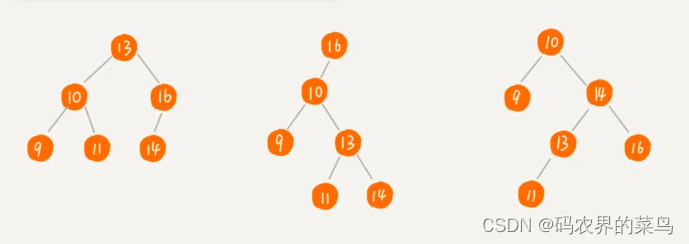
1. 二叉查找树的查找操作

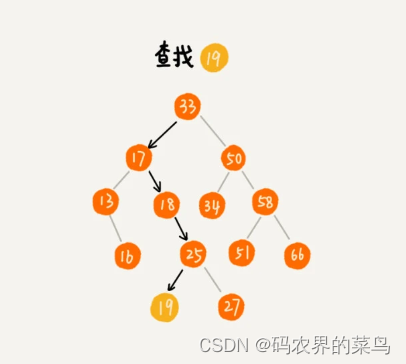
首先，我们看如何在二叉查找树中查找一个节点。我们先取根节点，如果它等于我们要查找的数据，那就返回。如果要查找的数据比根节点的值小，那就在左子树中递归查找；如果要查找的数据比根节点的值大，那就在右子树中递归查找。

2. 二叉查找树的插入操作

二叉查找树的插入过程有点类似查找操作。新插入的数据一般都是在叶子节点上，所以我们只需要从根节点开始，依次比较要插入的数据和节点的大小关系。

如果要插入的数据比节点的数据大，并且节点的右子树为空，就将新数据直接插到右子节点的位置；如果不为空，就再递归遍历右子树，查找插入位置。同理，如果要插入的数据比节点数值小，并且节点的左子树为空，就将新数据插入到左子节点的位置；如果不为空，就再递归遍历左子树，查找插入位置。

3. 二叉查找树的删除操作

二叉查找树的查找、插入操作都比较简单易懂，但是它的删除操作就比较复杂了 。针对要删除节点的子节点个数的不同，我们需要分三种情况来处理。

第一种情况是，如果要删除的节点没有子节点，我们只需要直接将父节点中，指向要删除节点的指针置为 null。比如图中的删除节点 55。

第二种情况是，如果要删除的节点只有一个子节点（只有左子节点或者右子节点），我们只需要更新父节点中，指向要删除节点的指针，让它指向要删除节点的子节点就可以了。比如图中的删除节点 13。

第三种情况是，如果要删除的节点有两个子节点，这就比较复杂了。我们需要找到这个节点的右子树中的最小节点，把它替换到要删除的节点上。然后再删除掉这个最小节点，因为最小节点肯定没有左子节点（如果有左子结点，那就不是最小节点了），所以，我们可以应用上面两条规则来删除这个最小节点。比如图中的删除节点 18。

4.支持重复数据的二叉查找树

前面讲二叉查找树的时候，我们默认树中节点存储的都是数字。很多时候，在实际的软件开发中，我们在二叉查找树中存储的，是一个包含很多字段的对象。我们利用对象的某个字段作为键值（key）来构建二叉查找树。我们把对象中的其他字段叫作卫星数据。

前面我们讲的二叉查找树的操作，针对的都是不存在键值相同的情况。那如果存储的两个对象键值相同，这种情况该怎么处理呢？我这里有两种解决方法。

第一种方法比较容易。二叉查找树中每一个节点不仅会存储一个数据，因此我们通过链表和支持动态扩容的数组等数据结构，把值相同的数据都存储在同一个节点上。

第二种方法比较不好理解，不过更加优雅。

每个节点仍然只存储一个数据。在查找插入位置的过程中，如果碰到一个节点的值，与要插入数据的值相同，我们就将这个要插入的数据放到这个节点的右子树，也就是说，把这个新插入的数据当作大于这个节点的值来处理。

当要查找数据的时候，遇到值相同的节点，我们并不停止查找操作，而是继续在右子树中查找，直到遇到叶子节点，才停止。这样就可以把键值等于要查找值的所有节点都找出来。

public class BinarySearchTree {
  private Node tree;

  public Node find(int data) {
    Node p = tree;
    while (p != null) {
      if (data < p.data) p = p.left;
      else if (data > p.data) p = p.right;
      else return p;
    }
    return null;
  }
  
  public void insert(int data) {
    if (tree == null) {
      tree = new Node(data);
      return;
    }

    Node p = tree;
    while (p != null) {
      if (data > p.data) {
        if (p.right == null) {
          p.right = new Node(data);
          return;
        }
        p = p.right;
      } else { // data < p.data
        if (p.left == null) {
          p.left = new Node(data);
          return;
        }
        p = p.left;
      }
    }
  }

  public void delete(int data) {
    Node p = tree; // p指向要删除的节点，初始化指向根节点
    Node pp = null; // pp记录的是p的父节点
    while (p != null && p.data != data) {
      pp = p;
      if (data > p.data) p = p.right;
      else p = p.left;
    }
    if (p == null) return; // 没有找到

    // 要删除的节点有两个子节点
    if (p.left != null && p.right != null) { // 查找右子树中最小节点
      Node minP = p.right;
      Node minPP = p; // minPP表示minP的父节点
      while (minP.left != null) {
        minPP = minP;
        minP = minP.left;
      }
      p.data = minP.data; // 将minP的数据替换到p中
      p = minP; // 下面就变成了删除minP了
      pp = minPP;
    }

    // 删除节点是叶子节点或者仅有一个子节点
    Node child; // p的子节点
    if (p.left != null) child = p.left;
    else if (p.right != null) child = p.right;
    else child = null;

    if (pp == null) tree = child; // 删除的是根节点
    else if (pp.left == p) pp.left = child;
    else pp.right = child;
  }

  public Node findMin() {
    if (tree == null) return null;
    Node p = tree;
    while (p.left != null) {
      p = p.left;
    }
    return p;
  }

  public Node findMax() {
    if (tree == null) return null;
    Node p = tree;
    while (p.right != null) {
      p = p.right;
    }
    return p;
  }
  
  public static class Node {
    private int data;
    private Node left;
    private Node right;

    public Node(int data) {
      this.data = data;
    }
  }
}

红黑树

红黑树其实是一种非常特殊的二叉查找树，由于二叉查找树在频繁的动态更新过程中，可能会出现树的高度远大于 log2n 的情况，从而导致各个操作的效率下降。极端情况下，二叉树会退化为链表，时间复杂度会退化到 O(n)。要解决这个复杂度退化的问题，我们需要设计一种平衡二叉查找树，而我们工程中最常用的平衡二叉查找树，其实就是红黑树。

什么是“平衡二叉查找树”

平衡二叉树的严格定义是这样的：二叉树中任意一个节点的左右子树的高度相差不能大于 1。从这个定义来看，上一节我们讲的完全二叉树、满二叉树其实都是平衡二叉树，但是非完全二叉树也有可能是平衡二叉树。

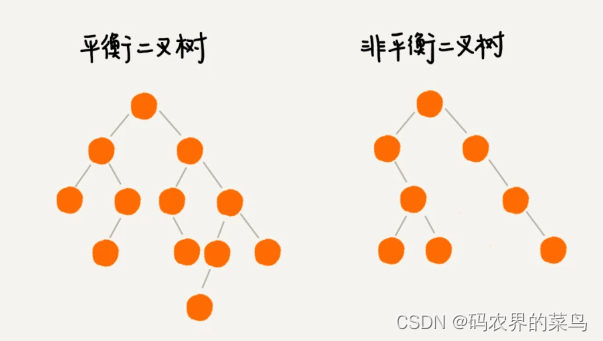
平衡二叉查找树不仅满足上面平衡二叉树的定义，还满足二叉查找树的特点。

但是很多平衡二叉查找树其实并没有严格符合上面的定义（树中任意一个节点的左右子树的高度相差不能大于 1），比如我们下面要讲的红黑树，它从根节点到各个叶子节点的最长路径，有可能会比最短路径大一倍。

我们学习数据结构和算法是为了应用到实际的开发中的，所以，我觉得没必去死抠定义。对于平衡二叉查找树这个概念，我觉得我们要从这个数据结构的由来，去理解“平衡”的意思。

发明平衡二叉查找树这类数据结构的初衷是，解决普通二叉查找树在频繁的插入、删除等动态更新的情况下，出现时间复杂度退化的问题。

所以，平衡二叉查找树中“平衡”的意思，其实就是让整棵树左右看起来比较“对称”、比较“平衡”，不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些，相应的插入、删除、查找等操作的效率高一些。

所以，如果我们现在设计一个新的平衡二叉查找树，只要树的高度不比 log2n 大很多（比如树的高度仍然是对数量级的），尽管它不符合我们前面讲的严格的平衡二叉查找树的定义，但我们仍然可以说，这是一个合格的平衡二叉查找树。

如何定义一棵“红黑树”

红黑树的英文是“Red-Black Tree”，简称 R-B Tree。它是一种不严格的平衡二叉查找树。

顾名思义，红黑树中的节点，一类被标记为黑色，一类被标记为红色。除此之外，一棵红黑树还需要满足这样几个要求：

• 根节点是黑色的；
• 每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存储数据；
• 任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的；
• 每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点；

这里的第二点要求“叶子节点都是黑色的空节点”，稍微有些奇怪，它主要是为了简化红黑树的代码实现而设置的。

红黑树的节点怎么是红，怎么是黑，我们引入一篇博客来解释：
https://www.cnblogs.com/tiancai/p/9072813.html