一、红黑树

 

---

 

 1.1、红黑树的定义（左根右，根叶黑，不红红，黑路同）

        前提，对于一棵二叉排序树(或者说二叉搜索树)，如果满足以下定义则是红黑树：

        ①每个结点或是红色，或是黑色的。

        ②根结点是黑色的。

        ③叶结点 (虚构的外部结点、NULL结点) 都是黑色的。

        ④不存在两个相邻的红结点（即红结点的父结点和孩子结点均是黑色的)。

        ⑤对每个结点，从该结点到任一叶结点的简单路径上，所含黑结点的数量相同。

        简记为：左根右（二叉排序树），根叶黑，不红红，黑路同（黑高相同） 

        黑高bh：从某结点出发（不包括）到达叶节点的任一简单路径上的黑结点总数 

 

        补充︰

        红黑树中任意一个叶结点的深度 = 从根开始到叶子结点的简单路径上，所含的红+黑结点数之和，又根据第⑤点，那任意两个叶节点的深度差就等于从根开始到这两个叶节点所经过的红色节点数之差，这就解释了为什么红黑树的结点平衡因子的绝对值有可能远大于1。

 

---

 

1.2、 红黑树与平衡二叉树的比较

        红黑树和平衡二叉树：都是特殊的二叉排序树，且都是自平衡的(即插入和删除时会根据定义自发的调整树而不需要人手动调整)，树高都是O(logn)级别（树高可以认为和最坏情况下查找的时间是相等的)，插入和删除复杂度都是O(logn)。 

        平衡二叉树：对于平衡的要求更高（即平衡因子只能是-1，0，1)，树高一般比红黑树低

        插入和删除调整的次数更多，需要花费的时间更多。

        红黑树：的对于平衡的要求低一点，由红黑因子来限制（平衡因子的绝对值有可能大于1)，一般树高也会高于平衡二叉树,但插入和删除操作花的时间更少。

        时间复杂度：比如删除操作时间复杂度是O(logn)，考试中可以看作所花时间为C*logn，那红黑树和平衡二叉树的删除复杂度相等都是O(logn)，但红黑树所花时间更少，可以理解为他的常数C更小，请记住时间复杂度不是确定的数, 前面常数C的具体值是不确定的。

        

 

---

 

1.3、红黑树插入

         

 

• 父子如果都是红色就会吵架出问题(不红红)
• 新插入结点为红（根节点的话需要调整为黑)
• 若父亲为黑不需要调整
• 父亲为红时不满足红黑树性质,需要调整，两种情况
  • ①同辈(父和叔）有强有弱则同辈解决（按平衡二叉树规则旋转)
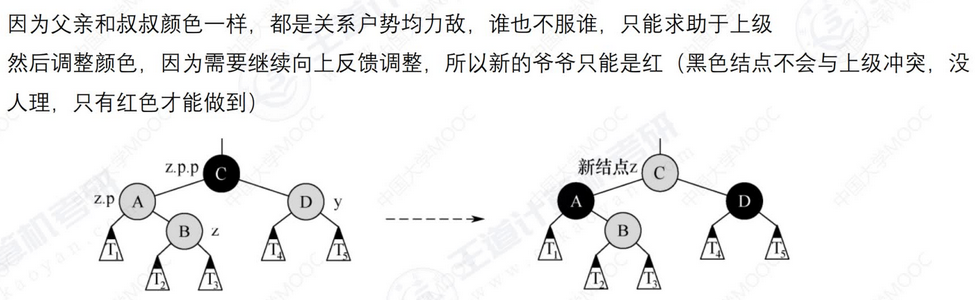
  • ②同辈势均力敌则交给长辈处理（都是红则把爷爷看作新节点上级去处理)
  • 要么旋转自己处理，要么交给长辈处理，且这两种情况都需要染色，根据是否需要交给长辈处理染色

         

 黑叔：

        

 红叔：

        

 

---

 

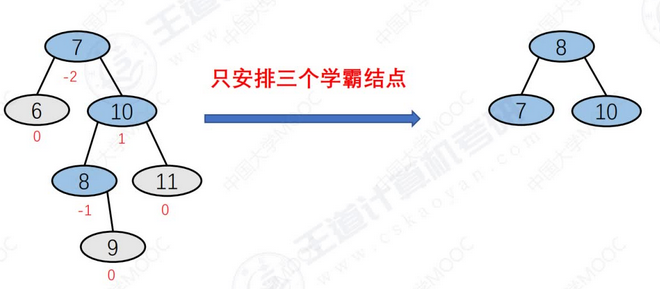
二、平衡二叉树旋转

 

 

 

---

 

---

 

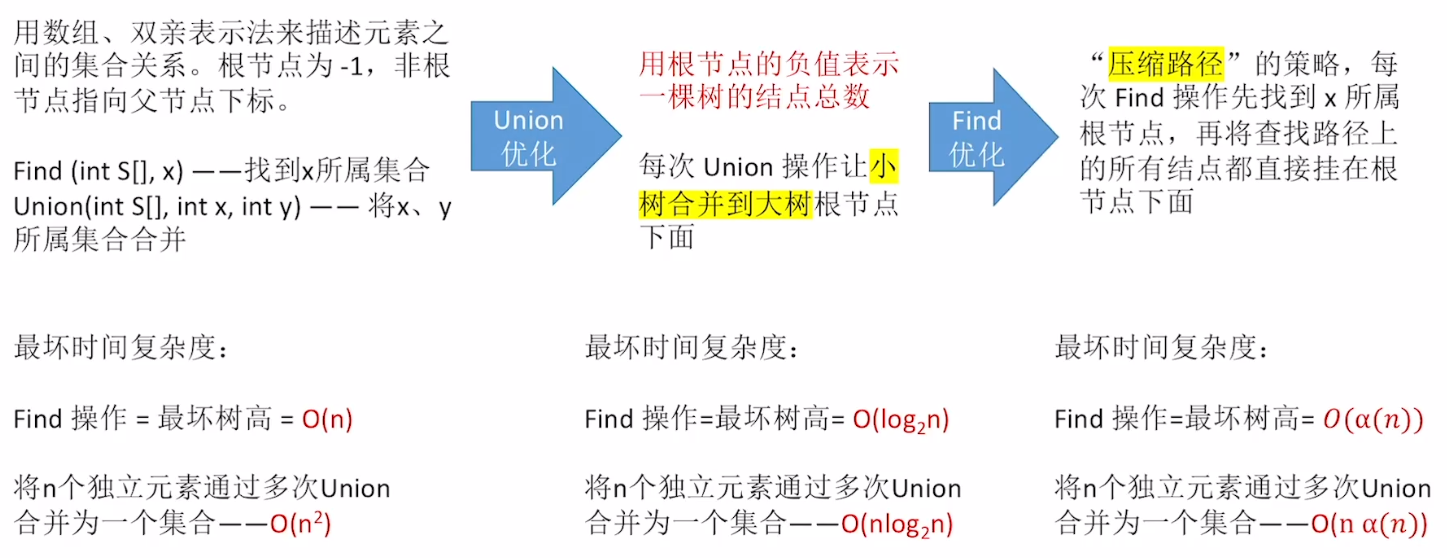
三、并查集

 

 

• 三要素
  • 逻辑结构 —— 集合
  • 初始化（所有数组元素初始化为-1）、查、并
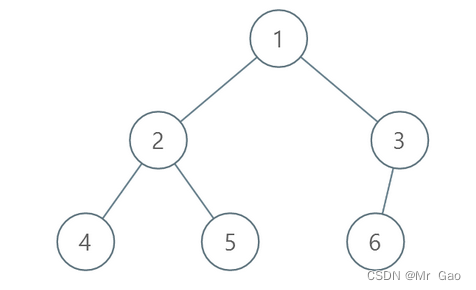
  • 存储结构 —— 顺序存储，双亲表示法
• 优化
  • 

 

---

内容参考于 —— 王道