2471. 逐层排序二叉树所需的最少操作数目-层次遍历+选择排序

给你一个 值互不相同 的二叉树的根节点 root 。

在一步操作中，你可以选择 同一层 上任意两个节点，交换这两个节点的值。

返回每一层按 严格递增顺序 排序所需的最少操作数目。

节点的 层数 是该节点和根节点之间的路径的边数。

示例 1 ：

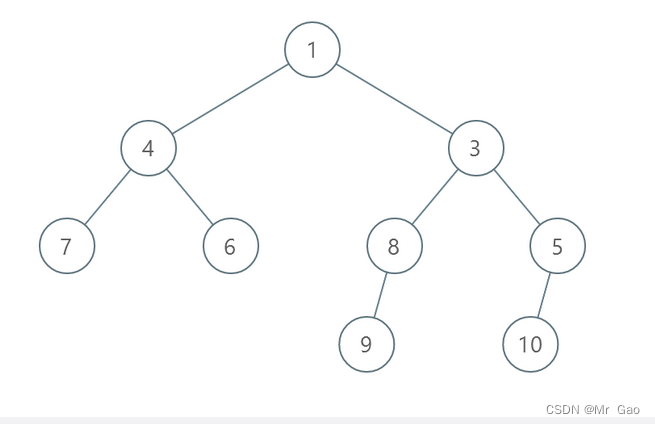
输入：root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
输出：3
解释：

• 交换 4 和 3 。第 2 层变为 [3,4] 。
• 交换 7 和 5 。第 3 层变为 [5,6,8,7] 。
• 交换 8 和 7 。第 3 层变为 [5,6,7,8] 。
  共计用了 3 步操作，所以返回 3 。
  可以证明 3 是需要的最少操作数目。

示例 2 ：

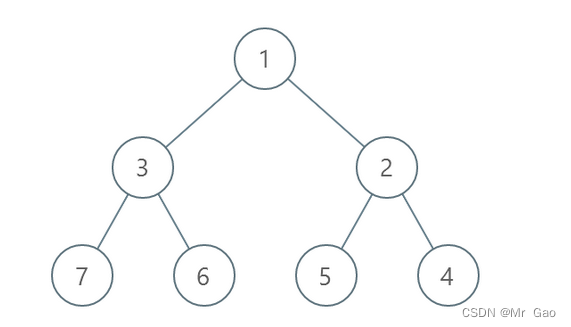
输入：root = [1,3,2,7,6,5,4]
输出：3
解释：

• 交换 3 和 2 。第 2 层变为 [2,3] 。
• 交换 7 和 4 。第 3 层变为 [4,6,5,7] 。
• 交换 6 和 5 。第 3 层变为 [4,5,6,7] 。
  共计用了 3 步操作，所以返回 3 。
  可以证明 3 是需要的最少操作数目。

示例 3 ：

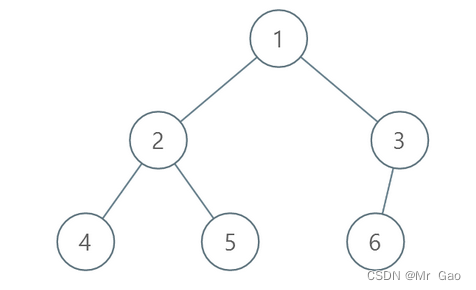
输入：root = [1,2,3,4,5,6]
输出：0
解释：每一层已经按递增顺序排序，所以返回 0 。

这题考法也是挺有新意的，解题代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
 #define size 100000
int  bubble_sort(int *a,int asize){
    if(asize==1){
        return 0;
    }
    int re=0;
    int r=0;
     for(int i=0;i<asize-1;i++){
         if(a[i]<=a[i+1]){
             r=1;
         }
     }
     if(r==0){
         return asize/2;
     }
   
    for(int i=0;i<asize-1;i++){
        int min_index=i;
         for(int j=i+1;j<asize;j++){
             if(a[j]<a[min_index]){
                 min_index=j;
             }
             
        }
        if(min_index!=i){
            re++;
            int t=a[min_index];
            a[min_index]=a[i];
            a[i]=t;

        }

    }
  //  printf("%d ",re);
   
    return re;

}
int minimumOperations(struct TreeNode* root){
    struct TreeNode* Q[size],*p;
    int front=0,rear=0;
    Q[rear]=root;
    rear=(rear+1)%size;
     Q[rear]=NULL;
    rear=(rear+1)%size;
    int count=0;
    int *a=(int *)malloc(sizeof(int)*size);
    int re=0;
    
    while(front!=rear){
        p=Q[front];
        front=(front+1)%size;
        if(p==NULL&&front!=rear){
             Q[rear]=NULL;
             rear=(rear+1)%size;
             re=re+ bubble_sort(a,count);
             count=0;
        }
       else if(p==NULL&&front==rear){
             re=re+ bubble_sort(a,count);
           break;
       }
       if(p){
           a[count++]=p->val;
           if(p->left){
               Q[rear]=p->left;
                rear=(rear+1)%size;
              

           }
           if(p->right){
                Q[rear]=p->right;
                rear=(rear+1)%size;
              
               
           }
       }

    }
    return re;





}