走进射线管积分：探索数学与现实世界的神秘桥梁

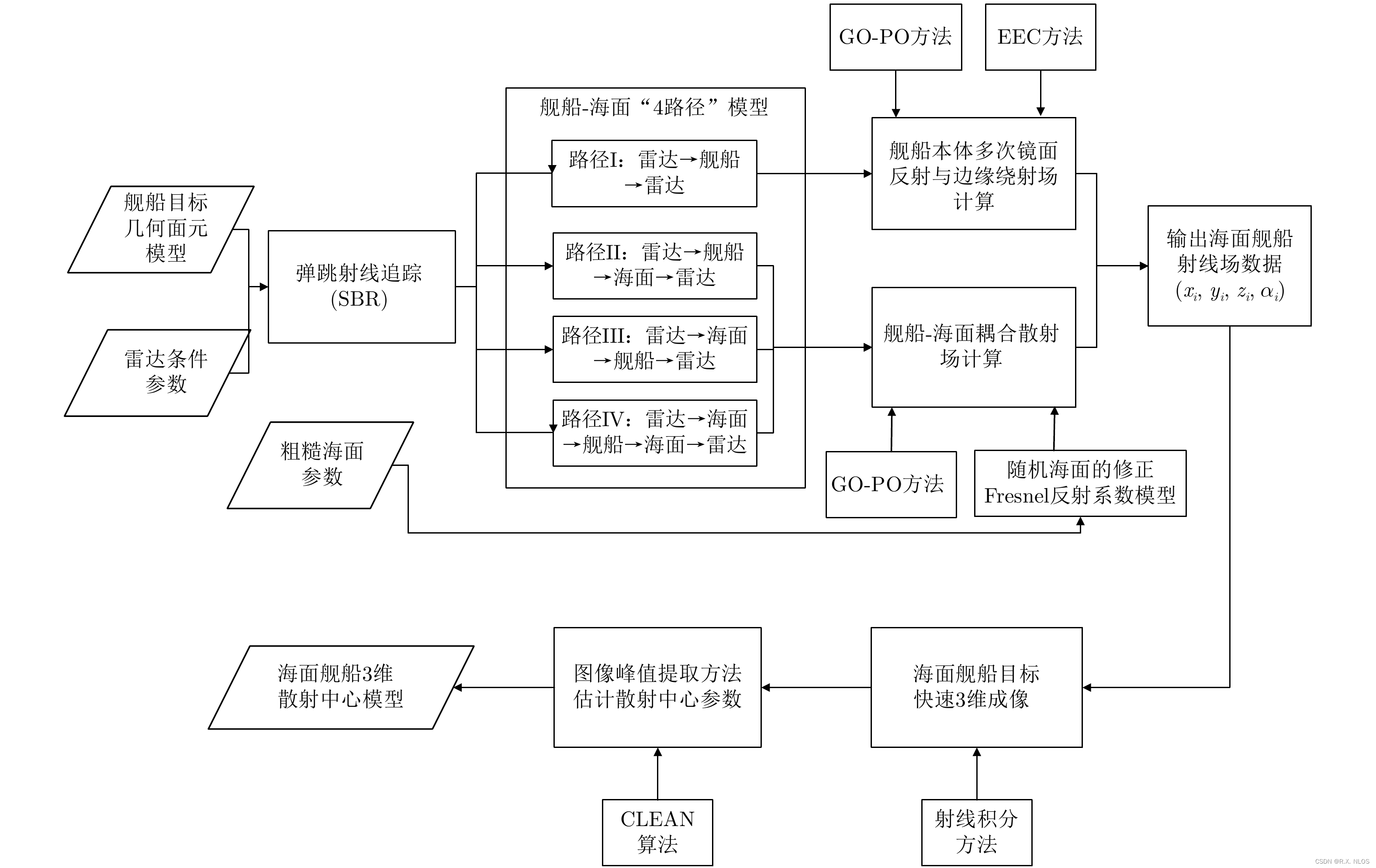
在这里插入图片描述

射线管积分雷达成像

射线管积分（Ray Tube Integration）是一种强大的数学工具，用于处理各种科学和工程问题。它的核心思想是将空间分割为一系列连续的射线管，并在每个射线管上进行积分，从而获得对整个空间的全面理解。

背景介绍

射线管积分的应用是多种多样的，包括电磁学、光学、声学等领域。它们是理解许多物理问题的基础，因为他们可以将复杂的空间问题简化为可解的一维问题。

例如，想象一束光线通过一个透明物体。我们可以把这个物体想象成一个由无数个射线管组成的集合，每个射线管都包含一条光线。通过分析每个射线管的光学性质，我们可以了解整个物体的光学行为。

这就像是我们试图理解一个复杂的森林。我们可能无法同时关注每一棵树，但是我们可以选择一条路径（或一束“射线”）穿过森林，然后重复这个过程，最终我们可以得到对整个森林的全面理解。

原理介绍和推导

射线管积分的基本定义是：

$\int Td\Omega = \int \int T ds d\Omega$

其中， $T$ 是一个标量或向量场， $d\Omega$ 是射线管的横截面积， $d s$ 是射线管的长度。

这个公式的推导基于微积分的基本原理。首先，我们需要定义一个新的积分测度 $d\Omega$ ，这个测度的定义是：

$d\Omega = \frac{dS}{r^2}$

其中， $d S$ 是射线管的实际面积， $r$ 是射线管的长度。这个测度的意义是，它衡量的是射线管的“视角”，而不是它的实际面积。

然后，我们可以用 $d\\Omega$ 来定义射线管的积分。这个积分的定义是：

$\int Td\Omega = \int \int T ds d\Omega$

这个公式的意义是，它计算的是场 $T$ 沿着射线管的积分。这是一个一维的积分，因此比在原始空间中计算积分要简单得多。

研究现状

尽管射线管积分的理论已经存在了一段时间，但是其在实践中的应用仍然在不断发展。例如，在电磁学中，射线管积分是理解和计算电磁波传播的关键工具。在光学中，射线管积分被用来分析复杂的光学系统，例如透镜和镜子。

近年来，射线管积分的应用在包括计算机图形学、无线通信、医疗成像等领域得到了扩展。在计算机图形学中，射线管积分被用来生成逼真的光照和阴影效果。在无线通信中，射线管积分被用来预测无线信号的传播路径和接收强度。在医疗成像中，射线管积分被用来重构从CT或MRI扫描中获取的数据。

挑战

尽管射线管积分具有强大的理论基础，但在实践应用中仍然面临一些挑战。首先，射线管积分需要对空间进行密集的分割，这在计算上可能十分昂贵。此外，射线管的选择和排列也会影响积分的精度。

其次，射线管积分通常假设场量在射线管内是均匀的，这可能不适用于所有情况。例如，在含有散射或反射的介质中，场量可能在射线管内变化。

这就像试图用一组直线来近似一条曲线。虽然我们可以通过增加直线的数量来提高近似的精度，但这会增加计算的复杂性。此外，如果曲线在某些地方弯曲得非常陡，那么直线近似可能无法准确地捕捉到这些变化。

未来展望

尽管存在这些挑战，但射线管积分的前景仍然十分广阔。随着计算资源的增加和新算法的开发，我们期待射线管积分在更多的领域得到应用。

例如，未来我们可能会看到射线管积分在人工智能、机器学习和数据科学中的应用。通过将射线管积分与这些领域的技术结合，我们可能能够解决一些传统上难以处理的问题，例如高维数据分析和复杂系统模拟。

代码示例

以下是一个使用Python和NumPy库实现的简单射线管积分的例子：

import numpy as np

# Define a simple scalar field
def field(x, y):
    return x**2 + y**2

# Define the integration path (a straight line)
x = np.linspace(-1, 1, 100)
y = np.zeros_like(x)

# Calculate the integral along the path
integral = np.trapz(field(x, y), x)

print('The integral is:', integral)