机器学习笔记之优化算法——Baillon Haddad Theorem简单认识
引言
本节将简单认识 Baillon Haddad Theorem \text{Baillon Haddad Theorem} Baillon Haddad Theorem(白老爹定理),并提供相关证明。
Baillon Haddad Theorem \text{Baillon Haddad Theorem} Baillon Haddad Theorem简单认识
如果函数
f
(
⋅
)
f(\cdot)
f(⋅)在其定义域内可微,并且是凸函数,则存在如下等价条件:
以下几个条件之间相互等价。
-
关于 f ( ⋅ ) f(\cdot) f(⋅)的梯度 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足 L \mathcal L L-利普希兹连续;
{ ∀ x , x ^ ∈ R n , ∃ L : s . t . ∣ ∣ f ( x ) − f ( x ^ ) ∣ ∣ ≤ L ⋅ ∣ ∣ x − x ^ ∣ ∣ ∃ ξ ∈ ( x , x ^ ) ⇒ ∣ ∣ f ( x ) − f ( x ^ ) ∣ ∣ ∣ ∣ x − x ^ ∣ ∣ = f ′ ( ξ ) ≤ L \begin{cases} \forall x,\hat x \in \mathbb R^n ,\exist \mathcal L: \quad s.t.||f(x) - f(\hat x)|| \leq \mathcal L \cdot ||x - \hat x|| \\ \quad \\ \begin{aligned} \exist \xi \in (x,\hat x) \Rightarrow \frac{||f(x) - f(\hat x)||}{||x - \hat x||} = f'(\xi) \leq \mathcal L \end{aligned} \end{cases} ⎩ ⎨ ⎧∀x,x^∈Rn,∃L:s.t.∣∣f(x)−f(x^)∣∣≤L⋅∣∣x−x^∣∣∃ξ∈(x,x^)⇒∣∣x−x^∣∣∣∣f(x)−f(x^)∣∣=f′(ξ)≤L
关于利普希兹连续详见二次上界引理。从逻辑的角度理解,这意味着:函数 f ( ⋅ ) f(\cdot) f(⋅)中斜率的变化量被利普希兹常数 L \mathcal L L约束。从图像的角度模糊观察,由于 L \mathcal L L的限制,不会出现斜率过于陡峭的情况。
见下图。从x ⇒ y x \Rightarrow y x⇒y的过程中,∇ f ( x ) ⇒ ∇ f ( y ) \nabla f(x) \Rightarrow \nabla f(y) ∇f(x)⇒∇f(y)发生了剧烈的变化。这本质上说明f ( ⋅ ) f(\cdot) f(⋅)在[ x , y ] [x,y] [x,y]区间内过于陡峭的原因。

-
关于函数 G ( x ) = L 2 x T x − f ( x ) \begin{aligned}\mathcal G(x) = \frac{\mathcal L}{2} x^T x - f(x)\end{aligned} G(x)=2LxTx−f(x)同样是凸函数。
观察 G ( x ) \mathcal G(x) G(x),可以发现它由两部分组成:系数是 L 2 \begin{aligned}\frac{\mathcal L}{2}\end{aligned} 2L,关于变量 x x x的二次项结果;以及 f ( x ) f(x) f(x)自身。而二次函数 L 2 x T x \begin{aligned}\frac{\mathcal L}{2}x^Tx\end{aligned} 2LxTx其自身一定是个凸函数。该条件意味着:这两个凸函数的差也是凸函数。
如果从逻辑角度对 L 2 x T x − f ( x ) \begin{aligned}\frac{\mathcal L}{2}x^Tx - f(x)\end{aligned} 2LxTx−f(x)进行认知:两个凸函数之间做减法,若 f ( x ) f(x) f(x)的陡峭程度要高于 L 2 x T x \begin{aligned}\frac{\mathcal L}{2}x^Tx\end{aligned} 2LxTx,这势必使得减法结果可能不是凸函数;因而该等价条件的本质依然是:约束 f ( x ) f(x) f(x)斜率的变化率,而该变化率的约束与利普希兹常数 L \mathcal L L存在关联关系。
-
关于函数的梯度 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)具有余强制性 ( Co-coercive ) (\text{Co-coercive}) (Co-coercive)。即:
[ ∇ f ( x ) − ∇ f ( y ) ] T ( x − y ) ≥ 1 L ∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ 2 \left[\nabla f(x) - \nabla f(y)\right]^T(x - y) \geq \frac{1}{\mathcal L} ||\nabla f(x) - \nabla f(y)||^2 [∇f(x)−∇f(y)]T(x−y)≥L1∣∣∇f(x)−∇f(y)∣∣2
首先解释一下强制性 ( Coercive ) (\text{Coercive}) (Coercive)。它也被称作强单调性 ( Strongly monotonicity ) (\text{Strongly monotonicity}) (Strongly monotonicity)。从名字可以看出来——它比一般的单调性更强。关于 f ( ⋅ ) : R ↦ R f(\cdot) :\mathbb R \mapsto \mathbb R f(⋅):R↦R,其单调性的定义表示为:自变量的差异性与对应函数差异性之间同号。关于n n n维的特征空间f ( ⋅ ) : R n ↦ R n f(\cdot):\mathbb R^n \mapsto \mathbb R^n f(⋅):Rn↦Rn,那么此时的f ( x ) − f ( y ) f(x) - f(y) f(x)−f(y)与x − y x - y x−y都是向量。对应单调性的定义即:[ f ( x ) − f ( y ) ] T ( x − y ) ≥ 0 [f(x) - f(y)]^T(x - y) \geq 0 [f(x)−f(y)]T(x−y)≥0
∀ x , y ∈ R s . t . [ f ( x ) − f ( y ) ] ⋅ ( x − y ) ≥ 0 \forall x,y \in \mathbb R \quad s.t. [f(x) - f(y)] \cdot (x - y) \geq 0 ∀x,y∈Rs.t.[f(x)−f(y)]⋅(x−y)≥0
而强单调性在单调性同号的基础上,进行了更强的约束:将式子右侧的 0 0 0替换为一个恒正的值。该值通常表示为:系数 α \alpha α与 x x x的增量 ∣ ∣ x − y ∣ ∣ 2 ||x - y||^2 ∣∣x−y∣∣2的乘积形式:
[ f ( x ) − f ( y ) ] T ( x − y ) ≥ α ⋅ ∣ ∣ x − y ∣ ∣ 2 [f(x) - f(y)]^T (x - y) \geq \alpha \cdot ||x - y||^2 [f(x)−f(y)]T(x−y)≥α⋅∣∣x−y∣∣2
若该值使用 f ( x ) f(x) f(x)的增量进行表示,我们称之为余强制性,也被称作逆向强单调性 ( Inverse Strongly monotonicity ) (\text{Inverse Strongly monotonicity}) (Inverse Strongly monotonicity):
[ f ( x ) − f ( y ) ] T ( x − y ) ≥ α ⋅ ∣ ∣ f ( x ) − f ( y ) ∣ ∣ 2 [f(x) - f(y)]^T (x - y) \geq \alpha \cdot ||f(x) - f(y)||^2 [f(x)−f(y)]T(x−y)≥α⋅∣∣f(x)−f(y)∣∣2
回顾等价条件 3 3 3:不等式左侧就是 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)单调性的定义;不等式右侧则是关于余强制性的表述。需要关注的点在于:参与描述正值的系数 α \alpha α与利普希兹常数 L \mathcal L L之间存在关联关系: α = 1 L \begin{aligned}\alpha = \frac{1}{\mathcal L}\end{aligned} α=L1。
证明过程
通过证明:条件
1
⇒
1 \Rightarrow
1⇒条件
2
2
2,条件
2
⇒
2 \Rightarrow
2⇒条件
3
3
3,条件
3
⇒
3 \Rightarrow
3⇒条件
1
1
1来实现
3
3
3个条件之间的等价关系。
证明:条件 1 ⇒ 1 \Rightarrow 1⇒ 条件 2 2 2
若
f
(
⋅
)
f(\cdot)
f(⋅)是凸函数,在定义域内可微;并且梯度函数
∇
f
(
⋅
)
\nabla f(\cdot)
∇f(⋅)满足
L
\mathcal L
L-利普希兹连续,求证:函数
G
(
x
)
=
L
2
x
T
x
−
f
(
x
)
\begin{aligned}\mathcal G(x) = \frac{\mathcal L}{2} x^Tx - f(x)\end{aligned}
G(x)=2LxTx−f(x)是凸函数。
关于凸函数的一种证法在于,证明该函数的梯度满足单调性。之所以引入梯度的另一个原因是可以将
L
2
x
T
x
\begin{aligned}\frac{\mathcal L}{2} x^Tx\end{aligned}
2LxTx化成一次项。
证明过程:由
G
(
x
)
=
L
2
x
T
x
−
f
(
x
)
\begin{aligned}\mathcal G(x) = \frac{\mathcal L}{2} x^Tx -f(x)\end{aligned}
G(x)=2LxTx−f(x)可知,关于
G
(
x
)
\mathcal G(x)
G(x)梯度
∇
G
(
x
)
\nabla \mathcal G(x)
∇G(x)可表示为:
∇
G
(
x
)
=
L
⋅
x
−
∇
f
(
x
)
\nabla \mathcal G(x) = \mathcal L \cdot x - \nabla f(x)
∇G(x)=L⋅x−∇f(x)
至此,观察
∇
G
(
x
)
\nabla \mathcal G(x)
∇G(x)的单调性:
仅需证明
I
≥
0
\mathcal I \geq 0
I≥0恒成立即可。
∀
x
1
,
x
2
∈
R
n
⇒
I
=
[
∇
G
(
x
1
)
−
∇
G
(
x
2
)
]
T
(
x
1
−
x
2
)
\forall x_1,x_2 \in \mathbb R^n \Rightarrow \mathcal I = [\nabla \mathcal G(x_1) - \nabla \mathcal G(x_2)]^T (x_1 - x_2)
∀x1,x2∈Rn⇒I=[∇G(x1)−∇G(x2)]T(x1−x2)
将上述梯度结果代入,有:
继续展开~
I
=
[
L
⋅
x
1
−
∇
f
(
x
1
)
−
L
⋅
x
2
+
∇
f
(
x
2
)
]
T
(
x
1
−
x
2
)
=
L
⋅
(
x
1
−
x
2
)
T
(
x
1
−
x
2
)
−
[
∇
f
(
x
1
)
−
∇
f
(
x
2
)
]
T
(
x
1
−
x
2
)
\begin{aligned} \mathcal I & = [\mathcal L \cdot x_1 - \nabla f(x_1) - \mathcal L \cdot x_2 + \nabla f(x_2)]^T (x_1 - x_2) \\ & = \mathcal L\cdot (x_1 - x_2)^T(x_1 - x _2) - [\nabla f(x_1) - \nabla f(x_2)]^T(x_1 - x_2) \end{aligned}
I=[L⋅x1−∇f(x1)−L⋅x2+∇f(x2)]T(x1−x2)=L⋅(x1−x2)T(x1−x2)−[∇f(x1)−∇f(x2)]T(x1−x2)
观察后一项:
−
[
∇
f
(
x
1
)
−
∇
f
(
x
2
)
]
T
(
x
1
−
x
2
)
-[\nabla f(x_1) - \nabla f(x_2)]^T (x_1 - x_2)
−[∇f(x1)−∇f(x2)]T(x1−x2),这明显是两个向量的内积形式。可以根据柯西施瓦茨不等式,得到如下结果:
该部分同样可以使用向量乘法描述:
a
T
b
=
∣
a
∣
⋅
∣
b
∣
⋅
cos
θ
≤
∣
a
∣
⋅
∣
b
∣
a^Tb = |a|\cdot|b| \cdot \cos \theta \leq |a| \cdot |b|
aTb=∣a∣⋅∣b∣⋅cosθ≤∣a∣⋅∣b∣因为
cos
θ
∈
[
−
1
,
1
]
≤
1
\cos \theta \in [-1,1] \leq 1
cosθ∈[−1,1]≤1。
[
∇
f
(
x
1
)
−
∇
f
(
x
2
)
]
T
(
x
1
−
x
2
)
≤
∣
∣
∇
f
(
x
1
)
−
∇
f
(
x
2
)
∣
∣
⋅
∣
∣
x
1
−
x
2
∣
∣
[\nabla f(x_1) - \nabla f(x_2)]^T(x_1 - x_2) \leq ||\nabla f(x_1) - \nabla f(x_2)|| \cdot ||x_1 - x_2||
[∇f(x1)−∇f(x2)]T(x1−x2)≤∣∣∇f(x1)−∇f(x2)∣∣⋅∣∣x1−x2∣∣
加上负号与前一项,从而有:
至于
(
x
1
−
x
2
)
T
(
x
1
−
x
2
)
=
∣
∣
x
1
−
x
2
∣
∣
2
(x_1 - x_2)^T(x_1 - x_2) = ||x_1 - x_2||^2
(x1−x2)T(x1−x2)=∣∣x1−x2∣∣2,两向量重合,夹角为
0
0
0。
I
≥
L
⋅
∣
∣
x
1
−
x
2
∣
∣
2
−
∣
∣
∇
f
(
x
1
)
−
∇
f
(
x
2
)
∣
∣
⋅
∣
∣
x
1
−
x
2
∣
∣
\mathcal I \geq \mathcal L \cdot ||x_1 - x_2||^2 - ||\nabla f(x_1) - \nabla f(x_2)|| \cdot ||x_1 - x_2||
I≥L⋅∣∣x1−x2∣∣2−∣∣∇f(x1)−∇f(x2)∣∣⋅∣∣x1−x2∣∣
由于梯度函数
∇
f
(
⋅
)
\nabla f(\cdot)
∇f(⋅)满足
L
\mathcal L
L-利普希兹连续,因而将
∣
∣
∇
f
(
x
1
)
−
∇
f
(
x
2
)
∣
∣
≤
L
⋅
∣
∣
x
1
−
x
2
∣
∣
||\nabla f(x_1) - \nabla f(x_2)|| \leq \mathcal L \cdot ||x_1 - x_2||
∣∣∇f(x1)−∇f(x2)∣∣≤L⋅∣∣x1−x2∣∣,对上式中的
∣
∣
∇
f
(
x
1
)
−
∇
f
(
x
2
)
∣
∣
||\nabla f(x_1) - \nabla f(x_2)||
∣∣∇f(x1)−∇f(x2)∣∣进行替换,最终不等号的方向不发生变化:
{
−
∣
∣
∇
f
(
x
1
)
−
∇
f
(
x
2
)
∣
∣
≥
−
L
⋅
∣
∣
x
1
−
x
2
∣
∣
I
≥
L
⋅
∣
∣
x
1
−
x
2
∣
∣
2
−
∣
∣
∇
f
(
x
1
)
−
∇
f
(
x
2
)
∣
∣
⋅
∣
∣
x
1
−
x
2
∣
∣
≥
L
⋅
∣
∣
x
1
−
x
2
∣
∣
2
−
(
L
⋅
∣
∣
x
1
−
x
2
∣
∣
)
⋅
∣
∣
∣
x
1
−
x
2
∣
∣
=
0
\begin{cases} -||\nabla f(x_1) - \nabla f(x_2)|| \geq -\mathcal L \cdot ||x_1 - x_2|| \\ \quad \\ \begin{aligned} \mathcal I & \geq \mathcal L \cdot ||x_1 - x_2||^2 - ||\nabla f(x_1) - \nabla f(x_2)|| \cdot ||x_1 - x_2|| \\ & \geq \mathcal L \cdot ||x_1 - x_2||^2 - (\mathcal L \cdot ||x_1 - x_2||) \cdot |||x_1 - x_2|| \\ & = 0 \end{aligned} \end{cases}
⎩
⎨
⎧−∣∣∇f(x1)−∇f(x2)∣∣≥−L⋅∣∣x1−x2∣∣I≥L⋅∣∣x1−x2∣∣2−∣∣∇f(x1)−∇f(x2)∣∣⋅∣∣x1−x2∣∣≥L⋅∣∣x1−x2∣∣2−(L⋅∣∣x1−x2∣∣)⋅∣∣∣x1−x2∣∣=0
最终可证明: I ≥ 0 ⇒ \mathcal I \geq 0 \Rightarrow I≥0⇒梯度函数 ∇ G ( x ) \nabla \mathcal G(x) ∇G(x)有单调性。从而函数 G ( x ) \mathcal G(x) G(x)是凸函数。
证明:条件 3 ⇒ 3 \Rightarrow 3⇒条件 1 1 1
若梯度函数 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)有余强制性,那么该梯度函数 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足 L \mathcal L L-利普希兹连续。
证明过程:基于
∇
f
(
⋅
)
\nabla f(\cdot)
∇f(⋅)余强制性,结合柯西施瓦茨不等式,有:
使用柯西施瓦茨不等式将不等式左侧表示为模的乘积形式。
{
[
∇
f
(
x
)
−
∇
f
(
y
)
]
T
(
x
−
y
)
≥
1
L
∣
∣
∇
f
(
x
)
−
∇
f
(
y
)
∣
∣
2
⇓
∣
∣
∇
f
(
x
1
)
−
∇
f
(
x
2
)
∣
∣
⋅
∣
∣
x
1
−
x
2
∣
∣
≥
[
∇
f
(
x
1
)
−
∇
f
(
x
2
)
]
T
(
x
1
−
x
2
)
≥
1
L
∣
∣
∇
f
(
x
1
)
−
∇
f
(
x
2
)
∣
∣
2
\begin{cases} \begin{aligned} \left[\nabla f(x) - \nabla f(y)\right]^T(x - y) & \geq \frac{1}{\mathcal L} ||\nabla f(x) - \nabla f(y)||^2 \\ & \Downarrow \\ ||\nabla f(x_1) - \nabla f(x_2)|| \cdot ||x_1 - x_2|| & \geq [\nabla f(x_1) - \nabla f(x_2)]^T (x_1 - x_2) \\ & \geq \frac{1}{\mathcal L} ||\nabla f(x_1) - \nabla f(x_2)||^2 \end{aligned} \end{cases}
⎩
⎨
⎧[∇f(x)−∇f(y)]T(x−y)∣∣∇f(x1)−∇f(x2)∣∣⋅∣∣x1−x2∣∣≥L1∣∣∇f(x)−∇f(y)∣∣2⇓≥[∇f(x1)−∇f(x2)]T(x1−x2)≥L1∣∣∇f(x1)−∇f(x2)∣∣2
消去
∣
∣
∇
f
(
x
1
)
−
∇
f
(
x
2
)
∣
∣
||\nabla f(x_1) - \nabla f(x_2)||
∣∣∇f(x1)−∇f(x2)∣∣,整理有:
∣
∣
∇
f
(
x
1
)
−
∇
f
(
x
2
)
∣
∣
≤
L
⋅
∣
∣
x
1
−
x
2
∣
∣
||\nabla f(x_1) - \nabla f(x_2)|| \leq \mathcal L \cdot ||x_1 - x_2||
∣∣∇f(x1)−∇f(x2)∣∣≤L⋅∣∣x1−x2∣∣
从而得证:
∇
f
(
⋅
)
\nabla f(\cdot)
∇f(⋅)满足
L
\mathcal L
L-利普希兹连续。
证明:条件 2 ⇒ 2 \Rightarrow 2⇒条件 3 3 3
若 G ( x ) = L 2 x T x − f ( x ) \begin{aligned}\mathcal G(x) = \frac{\mathcal L}{2}x^Tx - f(x)\end{aligned} G(x)=2LxTx−f(x)是凸函数,那么关于梯度函数 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)有余强制性。
证明思路:在证明之前,引入几个辅助变量:
将余强制性不等式左侧
[
∇
f
(
x
1
)
−
∇
f
(
x
2
)
]
T
(
x
1
−
x
2
)
[\nabla f(x_1) - \nabla f(x_2)]^T (x_1 - x_2)
[∇f(x1)−∇f(x2)]T(x1−x2)记作
Δ
\Delta
Δ,并将其分解为如下形式:
其中将x 1 − x 2 x_1 - x_2 x1−x2转化成− ( x 2 − x 1 ) -(x_2 - x_1) −(x2−x1),并将负号提出来。其中[ ∇ f ( x 1 ) − ∇ f ( x 2 ) ] T = { [ ∇ f ( x 1 ) ] T − [ ∇ f ( x 2 ) ] T } [\nabla f(x_1) - \nabla f(x_2)]^T = \left\{[\nabla f(x_1)]^T - [\nabla f(x_2)]^T\right\} [∇f(x1)−∇f(x2)]T={[∇f(x1)]T−[∇f(x2)]T}。
Δ = [ f ( x 1 ) + f ( x 2 ) ] − [ f ( x 1 ) + f ( x 2 ) ] ⏟ = 0 − { [ ∇ f ( x 1 ) ] T − [ ∇ f ( x 2 ) ] T } ( x 2 − x 1 ) = f ( x 2 ) − { f ( x 1 ) + [ ∇ f ( x 1 ) ] T ( x 2 − x 1 ) } ⏟ Δ 1 + f ( x 1 ) − { f ( x 2 ) + [ ∇ f ( x 2 ) ] T ( x 1 − x 2 ) } ⏟ Δ 2 = Δ 1 + Δ 2 \begin{aligned} \Delta & = \underbrace{[f(x_1) + f(x_2)] - [f(x_1) + f(x_2)]}_{=0} - \left\{[\nabla f(x_1)]^T - [\nabla f(x_2)]^T\right\}(x_2 - x_1) \\ & = \underbrace{f(x_2) - \{f(x_1) + [\nabla f(x_1)]^T (x_2 - x_1)\}}_{\Delta_1} + \underbrace{f(x_1) - \left\{f(x_2) + [\nabla f(x_2)]^T(x_1 - x_2)\right\}}_{\Delta_2} \\ & = \Delta_1 + \Delta_2 \end{aligned} Δ==0 [f(x1)+f(x2)]−[f(x1)+f(x2)]−{[∇f(x1)]T−[∇f(x2)]T}(x2−x1)=Δ1 f(x2)−{f(x1)+[∇f(x1)]T(x2−x1)}+Δ2 f(x1)−{f(x2)+[∇f(x2)]T(x1−x2)}=Δ1+Δ2
可以在图像中描述出 Δ 1 , Δ 2 \Delta_1,\Delta_2 Δ1,Δ2的表示:
- 其中 f ( x 1 ) + [ ∇ f ( x 1 ) ] T ( x 2 − x 1 ) f(x_1) + [\nabla f(x_1)]^T (x_2 - x_1) f(x1)+[∇f(x1)]T(x2−x1)表示过点 x 1 x_1 x1的 f ( ⋅ ) f(\cdot) f(⋅)的切线,与 x = x 2 x= x_2 x=x2相交后,到点 x 2 x_2 x2的距离。见黄色实线部分;
- 对应 Δ 1 \Delta_1 Δ1则表示: f ( x 2 ) f(x_2) f(x2)与 f ( x 1 ) + [ ∇ f ( x 1 ) ] T ( x 2 − x 1 ) f(x_1) + [\nabla f(x_1)]^T (x_2 - x_1) f(x1)+[∇f(x1)]T(x2−x1)之间的距离差值。见红色实线部分。
- 同理,关于
Δ
2
\Delta_2
Δ2的图像描述表示为:
对应的Δ 2 \Delta_2 Δ2表示为图中的绿色实线部分。
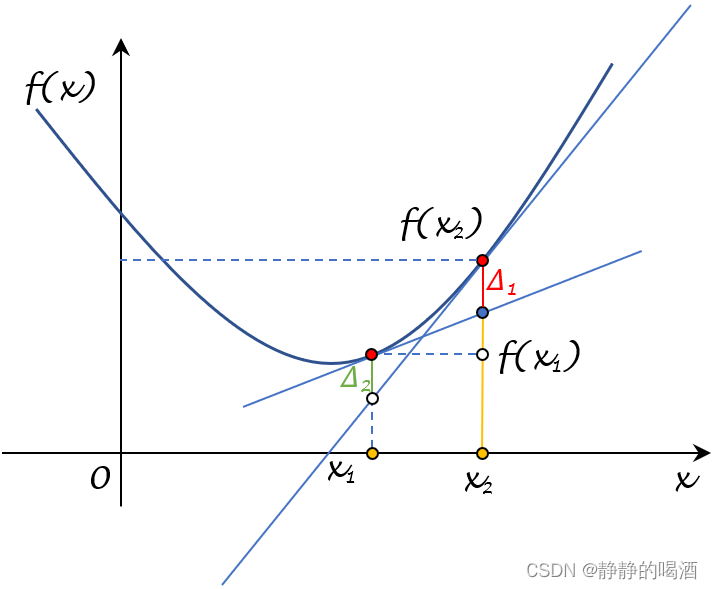
如果 Δ 1 \Delta_1 Δ1或者 Δ 2 \Delta_2 Δ2满足: Δ 1 ; Δ 2 ≥ 1 2 L ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ 2 \begin{aligned}\Delta_1;\Delta_2 \geq \frac{1}{2\mathcal L} ||\nabla f(x_1) - \nabla f(x_2)||^2\end{aligned} Δ1;Δ2≥2L1∣∣∇f(x1)−∇f(x2)∣∣2即可。
证明过程:
这里以
Δ
1
\Delta_1
Δ1为例,将
Δ
1
\Delta_1
Δ1展开,有:
Δ
1
=
f
(
x
2
)
−
[
∇
f
(
x
1
)
]
T
x
2
⏟
1
−
{
f
(
x
1
)
−
[
∇
f
(
x
1
)
]
T
x
1
}
⏟
2
\begin{aligned} \Delta_1 & = \underbrace{f(x_2) - [\nabla f(x_1)]^T x_2}_{1} - \underbrace{\left\{f(x_1) - [\nabla f(x_1)]^T x_1 \right\}}_{2} \end{aligned}
Δ1=1
f(x2)−[∇f(x1)]Tx2−2
{f(x1)−[∇f(x1)]Tx1}
可以发现,上述的
1
,
2
1,2
1,2两个部分存在相同的格式。因此假设一个函数:
关于函数
H
x
1
(
Z
)
\mathcal H_{x_1}(\mathcal Z)
Hx1(Z),其中
Z
\mathcal Z
Z是自变量,而内部的
x
1
x_1
x1被视作可变参数。
H
x
1
(
Z
)
=
f
(
Z
)
−
[
∇
f
(
x
1
)
]
T
Z
\mathcal H_{x_1}(\mathcal Z) = f(\mathcal Z) - [\nabla f(x_1)]^T \mathcal Z
Hx1(Z)=f(Z)−[∇f(x1)]TZ
从而
Δ
1
\Delta_1
Δ1可表示为:
Δ
1
=
H
x
1
(
x
2
)
−
H
x
1
(
x
1
)
\Delta_1 = \mathcal H_{x_1}(x_2) - \mathcal H_{x_1}(x_1)
Δ1=Hx1(x2)−Hx1(x1)
观察
H
x
1
(
Z
)
\mathcal H_{x_1}(\mathcal Z)
Hx1(Z)函数,其中
f
(
Z
)
f(\mathcal Z)
f(Z)是关于
Z
\mathcal Z
Z的凸函数;而
−
[
∇
f
(
x
1
)
]
T
Z
-[\nabla f(x_1)]^T \mathcal Z
−[∇f(x1)]TZ本质上是关于
Z
\mathcal Z
Z的一次函数,自然也是凸函数。根据保凸运算可知,
H
x
1
(
Z
)
\mathcal H_{x_1}(\mathcal Z)
Hx1(Z)一定是一个凸函数;并且由于
f
(
Z
)
f(\mathcal Z)
f(Z)与
−
[
∇
f
(
x
1
)
]
T
Z
-[\nabla f(x_1)]^T \mathcal Z
−[∇f(x1)]TZ均在
Z
\mathcal Z
Z定义域内可微,因而
H
x
1
(
Z
)
\mathcal H_{x_1}(\mathcal Z)
Hx1(Z)同样可微。因而
H
x
1
(
Z
)
\mathcal H_{x_1}(\mathcal Z)
Hx1(Z)关于
Z
\mathcal Z
Z的梯度
∇
H
x
1
(
Z
)
\nabla \mathcal H_{x_1}(\mathcal Z)
∇Hx1(Z)可表示为:
∇
H
x
1
(
Z
)
=
∇
f
(
Z
)
−
∇
f
(
x
1
)
\begin{aligned}\nabla \mathcal H_{x_1}(\mathcal Z) = \nabla f(\mathcal Z) - \nabla f(x_1) \end{aligned}
∇Hx1(Z)=∇f(Z)−∇f(x1)
当
Z
=
x
1
\mathcal Z = x_1
Z=x1时,有:
∇
H
x
1
(
x
1
)
=
0
\nabla \mathcal H_{x_1}(x_1) = 0
∇Hx1(x1)=0。这意味着:
Z
=
x
1
\mathcal Z = x_1
Z=x1是函数
H
x
1
(
Z
)
\mathcal H_{x_1}(\mathcal Z)
Hx1(Z)的极值点。而又因为
H
x
1
(
Z
)
\mathcal H_{x_1}(\mathcal Z)
Hx1(Z)的凸函数性质,因而该点一定是最小值点。记
H
x
1
(
Z
)
\mathcal H_{x_1}(\mathcal Z)
Hx1(Z)的最小值结果为
H
x
1
∗
\mathcal H_{x_1}^*
Hx1∗,从而可得:
H
x
1
∗
=
H
x
1
(
x
1
)
\mathcal H_{x_1}^* = \mathcal H_{x_1}(x_1)
Hx1∗=Hx1(x1)
根据条件
2
2
2:
G
(
Z
)
=
L
2
Z
T
Z
−
f
(
Z
)
\begin{aligned}\mathcal G(\mathcal Z) = \frac{\mathcal L}{2} \mathcal Z^T \mathcal Z - f(\mathcal Z) \end{aligned}
G(Z)=2LZTZ−f(Z)是凸函数,将
f
(
Z
)
=
H
x
1
(
Z
)
+
[
∇
f
(
x
1
)
]
T
Z
f(\mathcal Z) = \mathcal H_{x_1}(\mathcal Z) + [\nabla f(x_1)]^T \mathcal Z
f(Z)=Hx1(Z)+[∇f(x1)]TZ代入到条件
2
2
2中有:
这里将变量符号
x
x
x替换成变量符号
Z
\mathcal Z
Z,便于下面的计算,并将
Z
T
Z
\mathcal Z^T\mathcal Z
ZTZ使用
∣
∣
Z
∣
∣
2
||\mathcal Z||^2
∣∣Z∣∣2替代。
G
(
Z
)
=
L
2
∣
∣
Z
∣
∣
2
−
f
(
Z
)
=
L
2
∣
∣
Z
∣
∣
2
−
H
x
1
(
Z
)
−
[
∇
f
(
x
1
)
]
T
Z
⇒
G
(
Z
)
+
[
∇
f
(
x
1
)
]
T
Z
=
L
2
∣
∣
Z
∣
∣
2
−
H
x
1
(
Z
)
\begin{aligned} \mathcal G(\mathcal Z) & = \frac{\mathcal L}{2}||\mathcal Z||^2 - f(\mathcal Z) \\ & = \frac{\mathcal L}{2}||\mathcal Z||^2 - \mathcal H_{x_1}(\mathcal Z) - [\nabla f(x_1)]^T \mathcal Z \\ & \quad \\ \Rightarrow \mathcal G(\mathcal Z) + & [\nabla f(x_1)]^T \mathcal Z = \frac{\mathcal L}{2}||\mathcal Z||^2 - \mathcal H_{x_1}(\mathcal Z) \end{aligned}
G(Z)⇒G(Z)+=2L∣∣Z∣∣2−f(Z)=2L∣∣Z∣∣2−Hx1(Z)−[∇f(x1)]TZ[∇f(x1)]TZ=2L∣∣Z∣∣2−Hx1(Z)
观察上式的等号左侧:
G
(
Z
)
+
[
∇
f
(
x
1
)
]
T
Z
\mathcal G(\mathcal Z) + [\nabla f(x_1)]^T \mathcal Z
G(Z)+[∇f(x1)]TZ,同样可以如法炮制
H
x
1
(
Z
)
=
f
(
Z
)
+
[
∇
f
(
x
1
)
]
T
Z
\mathcal H_{x_1}(\mathcal Z) = f(\mathcal Z) + [\nabla f(x_1)]^T \mathcal Z
Hx1(Z)=f(Z)+[∇f(x1)]TZ一样,定义一个符号
G
x
1
(
Z
)
\mathcal G_{x_1}(\mathcal Z)
Gx1(Z),使得:
G
x
1
(
Z
)
=
G
(
Z
)
+
[
∇
f
(
x
1
)
]
T
Z
\mathcal G_{x_1}(\mathcal Z) = \mathcal G(\mathcal Z) + [\nabla f(x_1)]^T \mathcal Z
Gx1(Z)=G(Z)+[∇f(x1)]TZ
观察
G
x
1
(
Z
)
\mathcal G_{x_1}(\mathcal Z)
Gx1(Z)的相关性质:
- 关于第一项,根据条件 2 2 2描述: G ( Z ) \mathcal G(\mathcal Z) G(Z)自身是凸函数,可微;
- 关于第二项与 H x 1 ( Z ) \mathcal H_{x_1}(\mathcal Z) Hx1(Z)的第二项相同:关于 Z \mathcal Z Z的一次函数 [ ∇ f ( x 1 ) ] T Z [\nabla f(x_1)]^T \mathcal Z [∇f(x1)]TZ同样是凸函数,并在自身定义域内可微。
综上,依然可以根据保凸运算,关于函数
G
x
1
(
Z
)
\mathcal G_{x_1}(\mathcal Z)
Gx1(Z)也是凸函数,并在定义域内可微。从而该函数的梯度
∇
G
x
1
(
Z
)
\nabla \mathcal G_{x_1}(\mathcal Z)
∇Gx1(Z)表示如下:
∇
G
x
1
(
Z
)
=
L
2
⋅
2
⋅
Z
−
∇
H
x
1
(
Z
)
=
L
⋅
Z
−
∇
H
x
1
(
Z
)
\begin{aligned} \nabla \mathcal G_{x_1}(\mathcal Z) & = \frac{\mathcal L}{2} \cdot 2 \cdot \mathcal Z - \nabla \mathcal H_{x_1}(\mathcal Z) \\ & = \mathcal L \cdot \mathcal Z - \nabla \mathcal H_{x_1}(\mathcal Z) \end{aligned}
∇Gx1(Z)=2L⋅2⋅Z−∇Hx1(Z)=L⋅Z−∇Hx1(Z)
根据
G
x
1
(
Z
)
\mathcal G_{x_1}(\mathcal Z)
Gx1(Z)凸函数的性质,在
Z
\mathcal Z
Z定义域内取
z
1
≤
z
2
,
z
1
,
z
2
∈
R
z_1 \leq z_2,z_1,z_2 \in \mathbb R
z1≤z2,z1,z2∈R,必然有:
G
x
1
(
z
2
)
≥
G
x
1
(
z
1
)
+
[
∇
G
x
1
(
z
1
)
]
T
(
z
2
−
z
1
)
\mathcal G_{x_1}(z_2) \geq \mathcal G_{x_1}(z_1) + \left[\nabla \mathcal G_{x_1}(z_1)\right]^T(z_2 - z_1)
Gx1(z2)≥Gx1(z1)+[∇Gx1(z1)]T(z2−z1)
从上述图像中观察更加直观。也就是说:
Δ
1
≥
0
\Delta_1 \geq 0
Δ1≥0恒成立。将上述
G
x
1
(
Z
)
=
L
2
∣
∣
Z
∣
∣
2
−
H
x
1
(
Z
)
\begin{aligned}\mathcal G_{x_1}(\mathcal Z) = \frac{\mathcal L}{2}||\mathcal Z||^2 - \mathcal H_{x_1}(\mathcal Z)\end{aligned}
Gx1(Z)=2L∣∣Z∣∣2−Hx1(Z)代入,有:
L
2
∣
∣
z
2
∣
∣
2
−
H
x
1
(
z
2
)
⏟
G
x
1
(
z
2
)
≥
L
2
∣
∣
z
1
∣
∣
2
−
H
x
1
(
z
1
)
⏟
G
x
1
(
x
1
)
+
[
L
⋅
z
1
−
∇
H
x
1
(
z
1
)
]
T
⏟
[
G
x
1
(
z
1
)
]
T
⋅
(
z
2
−
z
1
)
\underbrace{\frac{\mathcal L}{2} ||z_2||^2 - \mathcal H_{x_1}(z_2)}_{\mathcal G_{x_1}(z_2)} \geq \underbrace{\frac{\mathcal L}{2}||z_1||^2 - \mathcal H_{x_1}(z_1)}_{\mathcal G_{x_1}(x_1)} + \underbrace{[\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1)]^T}_{[\mathcal G_{x_1}(z_1)]^T} \cdot (z_2 - z_1)
Gx1(z2)
2L∣∣z2∣∣2−Hx1(z2)≥Gx1(x1)
2L∣∣z1∣∣2−Hx1(z1)+[Gx1(z1)]T
[L⋅z1−∇Hx1(z1)]T⋅(z2−z1)
至此,描述
G
x
1
(
Z
)
\mathcal G_{x_1}(\mathcal Z)
Gx1(Z)凸函数性质的式子全部由
H
x
1
(
Z
)
\mathcal H_{x_1}(\mathcal Z)
Hx1(Z)进行代替。经过整理,有:
对比一下二次上界引理,它们确实比较相似,但并不是。因为
L
2
∣
∣
z
2
∣
∣
2
−
L
2
∣
∣
z
1
∣
∣
2
\begin{aligned}\frac{\mathcal L}{2}||z_2||^2 - \frac{\mathcal L}{2}||z_1||^2\end{aligned}
2L∣∣z2∣∣2−2L∣∣z1∣∣2与
L
2
∣
∣
z
2
−
z
1
∣
∣
2
\begin{aligned}\frac{\mathcal L}{2}||z_2 - z_1||^2\end{aligned}
2L∣∣z2−z1∣∣2绝大多数情况不相等。
H
x
1
(
z
2
)
≤
L
2
∣
∣
z
2
∣
∣
2
−
L
2
∣
∣
z
1
∣
∣
2
+
H
x
1
(
z
1
)
+
[
∇
H
x
1
(
z
1
)
−
L
⋅
z
1
]
T
(
z
2
−
z
1
)
\mathcal H_{x_1}(z_2) \leq \frac{\mathcal L}{2}||z_2||^2 - \frac{\mathcal L}{2} ||z_1||^2 + \mathcal H_{x_1}(z_1) + \left[\nabla \mathcal H_{x_1}(z_1) - \mathcal L \cdot z_1\right]^T(z_2 - z_1)
Hx1(z2)≤2L∣∣z2∣∣2−2L∣∣z1∣∣2+Hx1(z1)+[∇Hx1(z1)−L⋅z1]T(z2−z1)
但该式子并不影响我们使用二次上界引理中的操作:将
z
1
z_1
z1视作上一次迭代产生的数值解,因而
z
1
z_1
z1是已知项,从而不等式右侧是关于
z
2
z_2
z2的函数,记作
ϕ
(
z
2
)
\phi(z_2)
ϕ(z2):
H
x
1
(
z
2
)
≤
ϕ
(
z
2
)
≜
L
2
∣
∣
z
2
∣
∣
2
−
L
2
∣
∣
z
1
∣
∣
2
+
H
x
1
(
z
1
)
+
[
∇
H
x
1
(
z
1
)
−
L
⋅
z
1
]
T
(
z
2
−
z
1
)
\mathcal H_{x_1}(z_2) \leq \phi(z_2) \triangleq \frac{\mathcal L}{2}||z_2||^2 - \frac{\mathcal L}{2} ||z_1||^2 + \mathcal H_{x_1}(z_1) + \left[\nabla \mathcal H_{x_1}(z_1) - \mathcal L \cdot z_1\right]^T(z_2 - z_1)
Hx1(z2)≤ϕ(z2)≜2L∣∣z2∣∣2−2L∣∣z1∣∣2+Hx1(z1)+[∇Hx1(z1)−L⋅z1]T(z2−z1)
再次观察
ϕ
(
z
2
)
\phi(z_2)
ϕ(z2)中与
z
2
z_2
z2相关的项(其中仅与
z
1
z_1
z1相关的项被视作常数):
- L 2 ∣ ∣ z 2 ∣ ∣ 2 \begin{aligned}\frac{\mathcal L}{2}||z_2||^2\end{aligned} 2L∣∣z2∣∣2是关于 z 2 z_2 z2的二次项,是凸函数;且二次项系数 L 2 ≥ 0 \begin{aligned}\frac{\mathcal L}{2} \geq 0\end{aligned} 2L≥0,必然存在最小值;
- [ ∇ H x 1 ( z 1 ) − L ⋅ z 1 ] T ( z 2 − z 1 ) \left[\nabla \mathcal H_{x_1}(z_1) - \mathcal L \cdot z_1\right]^T(z_2 - z_1) [∇Hx1(z1)−L⋅z1]T(z2−z1)是关于 z 1 z_1 z1的一次函数,同样是凸函数。
最终通过保凸运算,能够确定
ϕ
(
z
2
)
\phi(z_2)
ϕ(z2)是一个凸二次函数。由于
H
x
1
(
z
2
)
≤
ϕ
(
z
2
)
\mathcal H_{x_1}(z_2) \leq \phi(z_2)
Hx1(z2)≤ϕ(z2),必然也小于
ϕ
(
z
2
)
\phi(z_2)
ϕ(z2)的最小值,也就是下界
inf
{
ϕ
(
z
2
)
}
=
min
ϕ
(
z
2
)
\inf \{\phi(z_2)\} = \mathop{\min} \phi(z_2)
inf{ϕ(z2)}=minϕ(z2):
H
x
1
(
z
2
)
≤
inf
{
ϕ
(
z
2
)
}
\mathcal H_{x_1}(z_2) \leq \inf \{\phi(z_2)\}
Hx1(z2)≤inf{ϕ(z2)}
下面关于
inf
{
ϕ
(
z
2
)
}
\inf\{\phi(z_2)\}
inf{ϕ(z2)}进行求解:
- 求解梯度
∇
ϕ
(
z
2
)
\nabla \phi(z_2)
∇ϕ(z2):
∇ ϕ ( z 2 ) = L ⋅ z 2 + ∇ H x 1 ( z 1 ) − L ⋅ z 1 \nabla \phi(z_2) = \mathcal L \cdot z_2 + \nabla \mathcal H_{x_1}(z_1) - \mathcal L \cdot z_1 ∇ϕ(z2)=L⋅z2+∇Hx1(z1)−L⋅z1 - 令
∇
ϕ
(
z
2
)
≜
0
\nabla \phi(z_2) \triangleq 0
∇ϕ(z2)≜0,有:
也就是说:ϕ ( z 2 ; m i n ) = min ϕ ( z 2 ) \phi(z_{2;min}) = \min \phi(z_2) ϕ(z2;min)=minϕ(z2)。
z 2 ; m i n = z 1 − ∇ H x 1 ( z 1 ) L z_{2;min} =z_1 - \frac{\nabla \mathcal H_{x_1}(z_1)}{\mathcal L} z2;min=z1−L∇Hx1(z1) - 将
z
2
;
m
i
n
z_{2;min}
z2;min带回原式,得到
min
ϕ
(
z
2
)
\min \phi(z_2)
minϕ(z2)有:
ϕ ( z 2 ; m i n ) = L 2 ∣ ∣ L ⋅ z 1 − ∇ H x 1 ( z 1 ) L ∣ ∣ 2 − L 2 ∣ ∣ z 1 ∣ ∣ 2 + H x 1 ( z 1 ) + [ ∇ H x 1 ( z 1 ) − L ⋅ z 1 ] T [ − ∇ H x 1 ( z 1 ) L ] \phi(z_{2;min}) = \frac{\mathcal L}{2} ||\frac{\mathcal L\cdot z_1 - \nabla \mathcal H_{x_1}(z_1)}{\mathcal L}||^2 - \frac{\mathcal L}{2}||z_1||^2 + \mathcal H_{x_1}(z_1) + [\nabla \mathcal H_{x_1}(z_1) - \mathcal L \cdot z_1]^T\left[- \frac{\nabla \mathcal H_{x_1}(z_1)}{\mathcal L}\right] ϕ(z2;min)=2L∣∣LL⋅z1−∇Hx1(z1)∣∣2−2L∣∣z1∣∣2+Hx1(z1)+[∇Hx1(z1)−L⋅z1]T[−L∇Hx1(z1)] - 很明显,只剩下了已知项
z
1
z_1
z1。整理有:
提出公因式1 2 L [ L ⋅ z 1 − ∇ H x 1 ( z 1 ) ] \begin{aligned}\frac{1}{2\mathcal L}[\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1)]\end{aligned} 2L1[L⋅z1−∇Hx1(z1)]使用乘法分配律~
ϕ ( z 2 ; m i n ) = 1 2 L ∣ ∣ L ⋅ z 1 − ∇ H x 1 ( z 1 ) ∣ ∣ 2 − L 2 ∣ ∣ z 1 ∣ ∣ 2 + H x 1 ( z 1 ) + 1 L [ L ⋅ z 1 − ∇ H x 1 ( z 1 ) ] T ∇ H x 1 ( z 1 ) = 1 2 L [ L ⋅ z 1 − ∇ H x 1 ( z 1 ) ] T { L ⋅ z 1 − ∇ H x 1 ( z 1 ) + 2 ∇ H x 1 ( z 1 ) } + h x 1 ( z 1 ) − L 2 ∣ ∣ z 1 ∣ ∣ 2 = 1 2 L [ L ⋅ z 1 − ∇ H x 1 ( z 1 ) ] T { L ⋅ z 1 + ∇ H x 1 ( z 1 ) } ⏟ 分配律 + h x 1 ( z 1 ) − L 2 ∣ ∣ z 1 ∣ ∣ 2 = 1 2 L [ L 2 ⋅ ∣ ∣ z 1 ∣ ∣ 2 − ∣ ∣ ∇ H x 1 ( z 1 ) ∣ ∣ 2 ] + H x 1 ( z 1 ) − L 2 ∣ ∣ z 1 ∣ ∣ 2 = H x 1 ( z 1 ) − 1 2 L ∣ ∣ ∇ H x 1 ( z 1 ) ∣ ∣ 2 \begin{aligned} \phi(z_{2;min}) & = \frac{1}{2\mathcal L}||\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1)||^2 - \frac{\mathcal L}{2}||z_1||^2 + \mathcal H_{x_1}(z_1) + \frac{1}{\mathcal L} [\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1)]^T \nabla \mathcal H_{x_1}(z_1) \\ & = \frac{1}{2\mathcal L} [\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1)]^T \left\{\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1) + 2 \nabla \mathcal H_{x_1}(z_1)\right\} + h_{x_1}(z_1) - \frac{\mathcal L}{2}||z_1||^2 \\ & = \frac{1}{2\mathcal L} \underbrace{[\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1)]^T \left\{\mathcal L \cdot z_1 + \nabla \mathcal H_{x_1}(z_1) \right\}}_{分配律} + h_{x_1}(z_1) - \frac{\mathcal L}{2}||z_1||^2 \\ & = \frac{1}{2\mathcal L} \left[\mathcal L^2 \cdot ||z_1||^2 - ||\nabla \mathcal H_{x_1}(z_1)||^2\right] + \mathcal H_{x_1}(z_1) - \frac{\mathcal L}{2}||z_1||^2 \\ & = \mathcal H_{x_1}(z_1) - \frac{1}{2\mathcal L}||\nabla \mathcal H_{x_1}(z_1)||^2 \end{aligned} ϕ(z2;min)=2L1∣∣L⋅z1−∇Hx1(z1)∣∣2−2L∣∣z1∣∣2+Hx1(z1)+L1[L⋅z1−∇Hx1(z1)]T∇Hx1(z1)=2L1[L⋅z1−∇Hx1(z1)]T{L⋅z1−∇Hx1(z1)+2∇Hx1(z1)}+hx1(z1)−2L∣∣z1∣∣2=2L1分配律 [L⋅z1−∇Hx1(z1)]T{L⋅z1+∇Hx1(z1)}+hx1(z1)−2L∣∣z1∣∣2=2L1[L2⋅∣∣z1∣∣2−∣∣∇Hx1(z1)∣∣2]+Hx1(z1)−2L∣∣z1∣∣2=Hx1(z1)−2L1∣∣∇Hx1(z1)∣∣2
至此,我们找到了关于
H
x
1
(
z
2
)
\mathcal H_{x_1}(z_2)
Hx1(z2)的二次上界:
H
x
1
(
z
2
)
≤
H
x
1
(
z
1
)
−
1
2
L
∣
∣
∇
H
x
1
(
z
1
)
∣
∣
2
\mathcal H_{x_1}(z_2) \leq \mathcal H_{x_1}(z_1) - \frac{1}{2\mathcal L}||\nabla \mathcal H_{x_1}(z_1)||^2
Hx1(z2)≤Hx1(z1)−2L1∣∣∇Hx1(z1)∣∣2
在
H
x
1
(
⋅
)
\mathcal H_{x_1}(\cdot)
Hx1(⋅)函数的收敛过程中,其最小值
H
x
1
∗
\mathcal H_{x_1}^*
Hx1∗必然有:
通过数值解只能无限接近最小值。
H
x
1
∗
≤
H
x
1
(
z
2
)
≤
H
x
1
(
z
1
)
−
1
2
L
∣
∣
∇
H
x
1
(
z
1
)
∣
∣
2
\mathcal H_{x_1}^* \leq \mathcal H_{x_1}(z_2) \leq \mathcal H_{x_1}(z_1) - \frac{1}{2\mathcal L}||\nabla \mathcal H_{x_1}(z_1)||^2
Hx1∗≤Hx1(z2)≤Hx1(z1)−2L1∣∣∇Hx1(z1)∣∣2
因为
H
x
1
(
⋅
)
\mathcal H_{x_1}(\cdot)
Hx1(⋅)函数在
x
1
x_1
x1处取得最小值:
H
x
1
(
x
1
)
=
H
x
1
∗
\mathcal H_{x_1}(x_1) = \mathcal H_{x_1}^*
Hx1(x1)=Hx1∗,并且
z
1
z_1
z1与
x
1
x_1
x1定义域相同,不妨设:
z
1
=
x
2
z_1 = x_2
z1=x2,有:
H
x
1
(
x
1
)
≤
H
x
1
(
x
2
)
−
1
2
L
∣
∣
∇
H
x
1
(
x
2
)
∣
∣
2
⇒
H
x
1
(
x
2
)
−
H
x
1
(
x
1
)
≥
1
2
L
∣
∣
∇
H
x
1
(
x
2
)
∣
∣
2
\begin{aligned} & \mathcal H_{x_1}(x_1) \leq \mathcal H_{x_1}(x_2) - \frac{1}{2\mathcal L}||\nabla \mathcal H_{x_1}(x_2)||^2 \\ \Rightarrow & \mathcal H_{x_1}(x_2) - \mathcal H_{x_1}(x_1) \geq \frac{1}{2\mathcal L}||\nabla \mathcal H_{x_1}(x_2)||^2 \end{aligned}
⇒Hx1(x1)≤Hx1(x2)−2L1∣∣∇Hx1(x2)∣∣2Hx1(x2)−Hx1(x1)≥2L1∣∣∇Hx1(x2)∣∣2
由于
Δ
1
=
H
x
1
(
x
2
)
−
H
x
1
(
x
1
)
\Delta_1 = \mathcal H_{x_1}(x_2) - \mathcal H_{x_1}(x_1)
Δ1=Hx1(x2)−Hx1(x1),因而最终有:
将
∇
H
x
1
(
Z
=
x
2
)
=
∇
f
(
x
2
)
−
∇
f
(
x
1
)
\nabla \mathcal H_{x_1}(\mathcal Z = x_2) = \nabla f(x_2) - \nabla f(x_1)
∇Hx1(Z=x2)=∇f(x2)−∇f(x1)代入:
Δ
1
≥
1
2
L
∣
∣
∇
H
x
1
(
x
2
)
∣
∣
2
=
1
2
L
∣
∣
∇
f
(
x
2
)
−
∇
f
(
x
1
)
∣
∣
2
=
1
2
L
∣
∣
∇
f
(
x
1
)
−
∇
f
(
x
2
)
∣
∣
2
\begin{aligned} \Delta_1 & \geq \frac{1}{2\mathcal L}||\nabla \mathcal H_{x_1}(x_2)||^2 \\ & = \frac{1}{2\mathcal L} ||\nabla f(x_2) - \nabla f(x_1)||^2 \\ & = \frac{1}{2\mathcal L} ||\nabla f(x_1) - \nabla f(x_2)||^2 \end{aligned}
Δ1≥2L1∣∣∇Hx1(x2)∣∣2=2L1∣∣∇f(x2)−∇f(x1)∣∣2=2L1∣∣∇f(x1)−∇f(x2)∣∣2
当然,这仅仅证明了一半,我们同样需要针对
Δ
2
\Delta_2
Δ2执行上述流程:
和上述流程完全相同,只不过可变参数由
x
1
x_1
x1变成了
x
2
x_2
x2,这里不再赘述。
Δ
2
=
[
f
(
x
1
)
−
f
(
x
2
)
]
−
{
[
∇
f
(
x
2
)
]
T
x
1
−
[
∇
f
(
x
2
)
]
T
x
2
}
=
f
(
x
1
)
−
[
∇
f
(
x
2
)
]
T
x
1
⏟
1
−
{
f
(
x
2
)
−
[
∇
f
(
x
2
)
]
T
x
2
}
⏟
2
=
H
x
2
(
x
1
)
−
H
x
2
(
x
2
)
\begin{aligned} \Delta_2 & = [f(x_1) - f(x_2)] - \left\{[\nabla f(x_2)]^T x_1 - [\nabla f(x_2)]^T x_2 \right\} \\ & = \underbrace{f(x_1) - [\nabla f(x_2)]^T x_1}_{1} - \underbrace{\{f(x_2) - [\nabla f(x_2)]^T x_2\}}_{2} \\ & = \mathcal H_{x_2}(x_1) - \mathcal H_{x_2}(x_2) \end{aligned}
Δ2=[f(x1)−f(x2)]−{[∇f(x2)]Tx1−[∇f(x2)]Tx2}=1
f(x1)−[∇f(x2)]Tx1−2
{f(x2)−[∇f(x2)]Tx2}=Hx2(x1)−Hx2(x2)
最终也可以得到一个类似结果:
Δ
2
≥
1
2
L
∣
∣
∇
f
(
x
1
)
−
∇
f
(
x
2
)
∣
∣
2
\Delta_2 \geq \frac{1}{2\mathcal L} ||\nabla f(x_1) - \nabla f(x_2)||^2
Δ2≥2L1∣∣∇f(x1)−∇f(x2)∣∣2
从而最终可得:
Δ
1
+
Δ
2
≥
2
⋅
1
2
L
∣
∣
∇
f
(
x
1
)
−
∇
f
(
x
2
)
∣
∣
2
=
1
L
∣
∣
∇
f
(
x
1
)
−
∇
f
(
x
2
)
∣
∣
2
\begin{aligned} \Delta_1 + \Delta_2 & \geq 2 \cdot \frac{1}{2\mathcal L}||\nabla f(x_1) - \nabla f(x_2)||^2 \\ & = \frac{1}{\mathcal L} ||\nabla f(x_1) - \nabla f(x_2)||^2 \end{aligned}
Δ1+Δ2≥2⋅2L1∣∣∇f(x1)−∇f(x2)∣∣2=L1∣∣∇f(x1)−∇f(x2)∣∣2
即:
[
∇
f
(
x
1
)
−
∇
f
(
x
2
)
]
T
(
x
1
−
x
2
)
≥
1
L
∣
∣
∇
f
(
x
1
)
−
∇
f
(
x
2
)
∣
∣
2
[\nabla f(x_1) - \nabla f(x_2)]^T(x_1 - x_2) \geq \frac{1}{\mathcal L} ||\nabla f(x_1) - \nabla f(x_2)||^2
[∇f(x1)−∇f(x2)]T(x1−x2)≥L1∣∣∇f(x1)−∇f(x2)∣∣2
即梯度函数
∇
f
(
⋅
)
\nabla f(\cdot)
∇f(⋅)具备余强制性,证毕。
相关参考:
【优化算法】梯度下降法-白老爹定理(上)
【优化算法】梯度下降法-白老爹定理(下)