本篇特征值、特征向量笔记来源于MIT线性代数课程。

矩阵特征值与特征向量

• ✨引言
• ✨什么是特征向量呢？
• ✨表示
• ✨从特例看特征值与特征向量
• ✨如何求解方程
• ▶️ 思路：
• ✨对称矩阵例子：
• ✨对比观察两个矩阵及它们的特征值及特征向量：
• ✨旋转矩阵例子 =>复数特征值：

✨引言

对于方阵而言，现在要找一些特殊的数字，即特征值，和特殊的向量，即特征向量。

✨什么是特征向量呢？

给定矩阵A，矩阵A作用在向量上，得到向量Ax（A的作用，作用在一个向量上，这其实就类似于函数，输入向量x，得到向量Ax）
在这些向量中，我们感兴趣的是一些特殊的向量，即变换前后方向一致的向量。
对于大多数向量而言，变换后的Ax是对于x是不同方向的，但是有特定的向量能使Ax平行于x。这些特殊的向量就是特征向量。

✨表示

$$\mathrm{A}x=\lambda x$$
$$\begin{gathered} 其中，\lambda 为一系数。可以与原来向量x的方向相同, \\ 也可以相反,即\lambda 可以为正，可以为负，也可以为0。 \\ (\lambda 也甚至可以是复数) \end{gathered}$$
在上述方程中，
$$x就是特征向量，\lambda 就是特征值。$$

✨从特例看特征值与特征向量

1️⃣投影矩阵
给定一个平面M，投影矩阵P作用于三维空间中所有的向量，那么哪些是P的特征向量呢？
一，在平面M上的任意向量，经过投影矩阵的作用，这些向量的长度和方向不变，$$Px=x$$
即特征值为1。
二，任意垂直于平面M的向量，经过投影矩阵的作用，这些向量的方向不变，长度变为0，$$Px=0$$
即特征值为0。
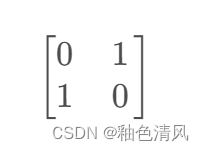
2️⃣矩阵A，交换向量的两个元素
$$\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]$$
特征值为1的特征向量
$$\left[\begin{array}{c}1\\ 1\end{array}\right]$$
特征值为-1的特征向量
$$\left[\begin{array}{c}1\\ -1\end{array}\right]$$

✨你发现了吗？
属于两个不同特征值的特征向量是垂直的！

✨引入：特征值的性质
n阶矩阵有n个特征值，在找这些特征值的时候，这里有一个特别的性质：
特征值之和等于矩阵元素对角线元素之和。(矩阵对角线元素之和也成为迹)
$${\lambda }_1+{\lambda }_2+\dots \dots +{\lambda }_n=a_{11}+a_{22}+\dots \dots +a_{nn}$$

在上述这个2阶矩阵中，若已知一个特征值为1，矩阵对角线元素之和为0，则可以知道另一个特征值为-1。

✨如何求解方程

$$\mathrm{A}x=\lambda x$$
首先，我们先将此移向：
$$(\mathrm{A}-\lambda I)x=0$$
$$\begin{gathered} \lambda 未知，x未知，但是对于不为0向量的x来说， \\ 这个式子说明了一点 \\ 一个矩阵，即\mathrm{A}-\lambda I作用于一个不为零的向量x后 \\ 向量变成了0，那么这个矩阵是奇异矩阵 \end{gathered}$$

奇异矩阵的性质:
奇异矩阵的行列式为0
非奇异矩阵（等价）：
1.行列式不为0
2.矩阵是满秩的
3.矩阵是可逆的

$$故可得，|\mathrm{A}-\lambda I|=0$$
由此，上述这个式子中就不含x了，从而得到一个关于$$\lambda$$的一个方程，该方程叫做特征方程或者特征值方程。

---

▶️ 思路：

▶️$$\begin{gathered} 这时我们可以先根据特征方程解出\lambda , \\ 而且不止一个\lambda , \\ 对于n阶矩阵来说，它可能有n个\lambda , \\ \lambda 可以是不同的值，当然也可以有重复的值 \\ 甚至会是同一个\lambda 重复n次 \end{gathered}$$
▶️$$\begin{gathered} 当我们根据特征方程求解出所有的\lambda \\ 之后我们将一个\lambda 回代，这时 \\ 矩阵\mathrm{A}-\lambda I是奇异的。 \\ 求解x利用消元法（已知一个奇异矩阵寻找零空间） \end{gathered}$$

▶️对零空间的理解：
首先，零空间并不是维度为0.
零空间不会独立存在的，它依赖于某个特定的矩阵A而存在。
（拿上面来说，我们就是在寻找矩阵A的零空间，即在矩阵A的作用下被映射到零点的所有向量的集合）

---

$$求解\lambda$$

✨对称矩阵例子：

对于对称矩阵A
$$\left[\begin{array}{cc}3& 1\\ 1& 3\end{array}\right]$$
下面我们来求解它的特征值。
<=>
$$\left[\begin{array}{cc}3-\lambda & 1\\ 1& 3-\lambda \end{array}\right]=0$$
<=>
$$(3-\lambda {)}^2-1=0(1)$$
<=>
$${\lambda }^2-6\lambda +8=0(2)$$
<=>
$$(\lambda -2)(\lambda -4)=0(3)$$
<=>
$${\lambda }_1=4,{\lambda }_2=2$$
因此我们可以得到矩阵A的两个特征值2和4。

接下来我们来求特征向量：
根据$(\mathrm{A}-\lambda I)x=0$，我们已知$\lambda$，即已知$(\mathrm{A}-\lambda I)$这个矩阵，它是一个奇异矩阵，作用于$x$ 使之为零向量，则$x$是相应零空间中的向量。

▶️首先，我们先来求解特征值是4对应的特征向量
$$A-4I$$
<=>
$$=\left[\begin{array}{cc}3-4& 1\\ 1& 3-4\end{array}\right]$$
<=>
$$=\left[\begin{array}{cc}-1& 1\\ 1& -1\end{array}\right]$$
现在来找它的零空间$X_1$等于多少？
使得$(\mathrm{A}-{\lambda }_{1}I)X_1=0$
显然$X_1$=
$$\left[\begin{array}{c}1\\ 1\end{array}\right]$$
▶️接下来，我们先来求解特征值是2对应的特征向量
$$A-2I$$
<=>
$$=\left[\begin{array}{cc}3-2& 1\\ 1& 3-2\end{array}\right]$$
<=>
$$=\left[\begin{array}{cc}1& 1\\ 1& 1\end{array}\right]$$
接下来我们寻找它的零空间的向量$X_2$
通过观察，我们可以看出$X_2$为
$$\left[\begin{array}{c}1\\ -1\end{array}\right]$$

✨对比观察两个矩阵及它们的特征值及特征向量：

$$\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]$$
${\lambda }_1=-1,{\lambda }_2=1$
$$\left[\begin{array}{cc}3& 1\\ 1& 3\end{array}\right]=0(2)$$
${\lambda }_1=2,{\lambda }_2=4$
记第一个矩阵为$A_1$，第二个矩阵为$A_2$，则有
$$A_1+3I=A_2$$
$A_1和A_2特征向量相同$
且它们特征值的关系为:
$${\lambda }_{A11}+3={\lambda }_{A21}$$
$${\lambda }_{A12}+3={\lambda }_{A22}$$
这值得我们细细研究：
如果有：
$$\mathrm{A}x=\lambda x（1）$$
则
$$(\mathrm{A}+3I)x=Ax+3x=\lambda x+3x=(\lambda +3)x（2）$$
由此，我们可以得出，
特征向量$x$是两个矩阵共同的特征向量
由(2)，可得，$A+3I$的特征值为$\lambda +3$
由此，我们可以得出，若矩阵$A和B$存在$A=B+3\lambda$

✨旋转矩阵例子 =>复数特征值：

$$Q=\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$$
根据上面我们得到的结论，矩阵的两个特征值${\lambda }_1和{\lambda }_2$，特征值之和等于矩阵的迹(即矩阵的对角线元素之和)，特征值之积等于矩阵行列式的值，即
$${\lambda }_1+{\lambda }_2=0（1）$$
$${\lambda }_1{\lambda }_2=-1（2）$$
在复数域，我们解出：
$${\lambda }_1=i,{\lambda }_2=-i$$
研究它的意义在于，我们由原来的一个实矩阵，扩展至它的特征值为一对复数。
而出现复数的原因，我们可以直观理解为与矩阵的对称性有关。

相比于前面的举例提到的，如果矩阵是对称的，就不会有复数特征值。


如果我们规定矩阵是对称的或者接近对称的，那么特征值就是实数。
如果越不对称，就如上述的旋转矩阵Q，这种矩阵特征值为纯虚数。
这两种是极端情况。
那么其余的就是介于对称和反对称的矩阵，即部分对称，部分反对称。
举个例子：

$$\left[\begin{array}{cc}3& 1\\ 0& 3\end{array}\right]$$
对于这个矩阵，它的两个特征值：
$${\lambda }_1+{\lambda }_2=3+3=6（1）$$
$${\lambda }_1{\lambda }_2=3\ast 3-0=9（2）$$
从而，我们解出，
$${\lambda }_1=3，{\lambda }_2=3$$
当然，如果你直接观察出这是一个三角矩阵并了解它的性质，可以直接从矩阵得出它的特征值。
三角矩阵的特征值即为对角线的元素，从而，
$${\lambda }_1=3，{\lambda }_2=3$$