数学思维导图怎么画？数学思维导图可以帮助我们更好地组织和理解各种数学概念。不仅是学生和教师可以受益，数学思维导图也可以在研究和工作中发挥作用。这种工具可以帮助你清晰地表示各种数学概念和关系，并将它们可视化，以便更容易理解。那么今天就给大家介绍一下数学思维导图的绘制方法。

 

使用【迅捷画图】创建数学思维导图非常简单且易于使用。它提供了各种绘图模板和工具，让你可以轻松地创建各种类型的图表和图形。以下是一些有用的技巧和步骤，可以帮助你更好地创建数学思维导图：

第一步：选择合适的模板：在创建新文档时，选择“数学思维导图”模板。这将为你提供一个基本框架，以便开始添加各种形状和文本框，以表示不同的数学概念和关系。

 

第二步：使用各种形状和线条：使用不同的形状和线条来表示数学概念和关系。例如，你可以使用圆形来表示一个概念，使用箭头来表示两个概念之间的关系，使用线条来表示某个概念的属性。

 

第三步：使用颜色和图标：使用颜色和图标来帮助你更好地区分和理解各种数学概念。例如，你可以使用不同的颜色来表示不同的概念，使用图标来表示某个概念的属性。

 

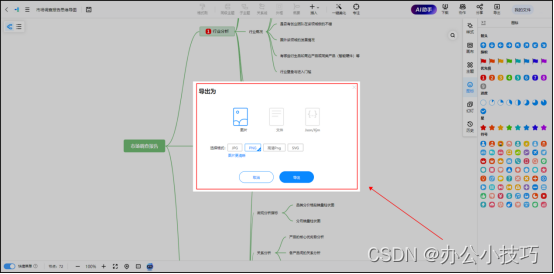
第四步：保存和共享：将导图保存为图像或PDF格式，以便在需要时轻松地共享和打印。你还可以将导图嵌入到文档或网页中，以便更好地展示和共享。

 

数学思维导图怎么画？总之，使用这款绘图工具创建数学思维导图非常简单且直观。