目录

摘要

论文阅读

1、标题和现存问题

2、准备知识

3、模型结构

4、实验准备

5、实验结果

深度学习

1、构建图数据

2、GCN模型

3、当前实验结果

总结

---

摘要

本周在论文阅读上，阅读了一篇时空图卷积网络:交通预测的深度学习框架的论文。文章的时空图卷积网络没有应用规则的卷积和递归单位，而是在图上公式化了问题，并建立了具有完整卷积结构的模型，从而可以以更少的参数更快的训练速度，实验结果表明模型十分优秀。在深度学习上，解决了之前遗留下的问题，并继续探究GCN。

This week,in terms of thesis reading,perusaling a paper on spatiotemporal graph convolutional networks: a deep learning framework for traffic prediction.The spatiotemporal graph convolutional network in the article does not apply regular convolution and recursive units, but formulates the problem on the graph and establishes a model with a complete convolutional structure, which can train faster with fewer parameters.The experimental results indicate that the model is very excellent.In deep learning, resolving the remaining issues and continued to explore GCN.

论文阅读

1、标题和现存问题

标题：时空图卷积网络:交通预测的深度学习框架

现存问题：以往对中长期流量预测的研究大致可以分为两大类:动态建模和数据驱动方法。动态建模为了达到稳态，仿真过程不仅需要复杂的系统编程，而且需要消耗大量的计算能力，模型的假设不实际和模型的简化也降低了预测的精度。经典的统计模型和机器学习模型是数据驱动方法的两个主要代表。这些方法对高度非线性的交通流具有约束可表示性。常规模型只能处理网格结构(如图像、视频)，而不能处理一般的域。同时，用于序列学习的递归网络需要迭代训练，这就引入了误差的逐步积累。

2、准备知识

交通预测是一个典型的时间序列预测问题，预测下一个H个时间步中最可能的交通度量值(如速度或交通流量)为:

 

在一个图上定义交通网络，并重点研究结构化的交通时间序列，每个 vt 表示时间步长为 t 的当前交通状态帧，以图结构数据矩阵的形式记录。

 

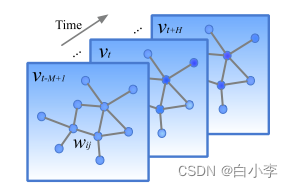
文章基于谱图卷积的概念引入了图卷积算子“∗G”的概念，即信号x∈Rn与核的乘积Θ：

 

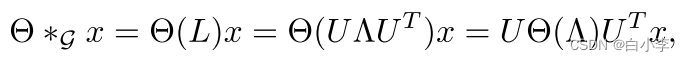
3、模型结构

STGCN由多个时空卷积块组成，每个卷积块形成一个“三明治”结构，中间有两个门控序列卷积层和一个空间图卷积层。

 

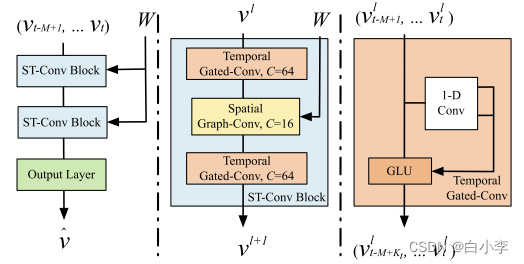
框架 STGCN由两个时空卷积块(ST-Conv块)和一个全连接的输出层组成。每个 ST-Conv 块包含两个时间门控卷积层和中间的一个空间图卷积层。在每个块内部采用剩余连接和瓶颈策略。

图的卷积可以写为：

 

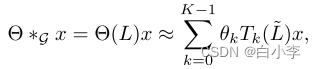
构造一个更深层的结构来恢复深度的空间信息，而不受限于由多项式给出的显式参数化。由于神经网络的缩放和归一化，我们可以进一步假设λmax≈2。因此，上式可以改写为：

 

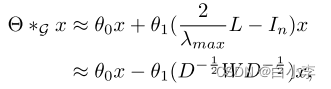
垂直应用具有一阶近似的图卷积堆栈，可以实现与水平方向上的k本地化卷积类似的效果，所有这些都利用了中心节点的(K−1)阶邻域的信息。在这种情况下，K是一个模型中连续的过滤操作或卷积层数。此外，分层线性结构是参数经济和高效的大规模图，因为近似的阶数限制在1。

文章在时间轴上采用整个卷积结构来捕捉交通流的时间动态行为。这种特殊的设计允许并行和可控的训练过程通过多层卷积结构形成的层次表示。时间卷积层包含一个一维的因果卷积，它带有一个宽度为kt的核，后面是一个非线性的门控线性单元(GLU)。对于图G中的每个节点，时间卷积在没有填充的情况下探索输入元素的Kt邻居，这导致序列的长度每次缩短Kt-1。因此，每个节点的时间卷积输入可以看作是一个长度为m的序列，时间门控卷积可以定义为:

 

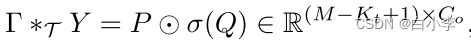
为了融合时空特征，构造时空卷积块(ST-Conv块)，对图结构时间序列进行联合处理。区块本身可以根据特定情况的规模和复杂性进行堆叠或扩展。模型中间的空间层是连接两个时间层的桥梁，时间层通过时间卷积实现从图卷积到空间状态的快速传播。“三明治”结构也有助于网络充分应用瓶颈策略，通过图卷积层对信道C进行降尺度和升尺度，实现尺度压缩和特征压缩。在每个ST-Conv块内采用层归一化，防止过拟合。对于block的输入输出：

 

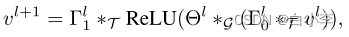
STGCN用于流量预测的损失函数为:

 

模型STGCN的主要特征总结如下:

•STGCN是一种处理结构化时间序列的通用框架。它不仅可以解决交通网络建模和预测问题，而且可以应用于更一般的时空序列学习任务。

•时空块结合了图形卷积和门控时间卷积，可以提取最有用的空间特征，并连贯地捕获最本质的时间特征。

•该模型完全由卷积结构组成，因此以更少的参数和更快的训练速度实现了对输入的并行化。更重要的是，这种经济架构允许模型以更高的效率处理大规模网络

4、实验准备

数据集： BJER4 是用双环探测器从北京市东四环主要区域采集的。

PeMSD7 是由部署在加利福尼亚州高速公路系统主要城市地区的39000 多个传感器站实时收集到的。

两个数据集的标准时间间隔设置为 5 分钟。因此，道路图的每个节点每天包含 288 个数据点。数据清理后，用线性插值方法补全缺失值。另外，采用Z-Score方法对数据输入进行标准化处理。在BJER4 中，利用传感器站部署图构建了北京东四环线路系统的路网拓扑。通过对每条道路的隶属关系、方向和出发地点的整理， 环线系统可以数字化为有向图。

在PeMSD7 中，道路图的邻接矩阵是根据交通网络中车站之间的距离计算的。加权邻接矩阵W可以表示为:

 

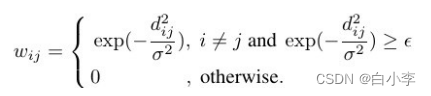
为了消除非典型交通，实验仅采用工作日的交通数据。。所有的测试都使用 60 分钟作为历史时间窗口，也就是 12 个观测数据点(M = 12)来预测未来15、30和45分钟(H = 3、6、9)的交通状况。

评估指标和基线测量和评估不同方法的性能，平均绝对误差(MAE)，平均绝对百分比误差(MAPE)，和均方根误差(RMSE)。

5、实验结果

不同方法在数据集BJER4上的性能比较：

 

不同方法在数据集PeMSD7上的性能比较：

 

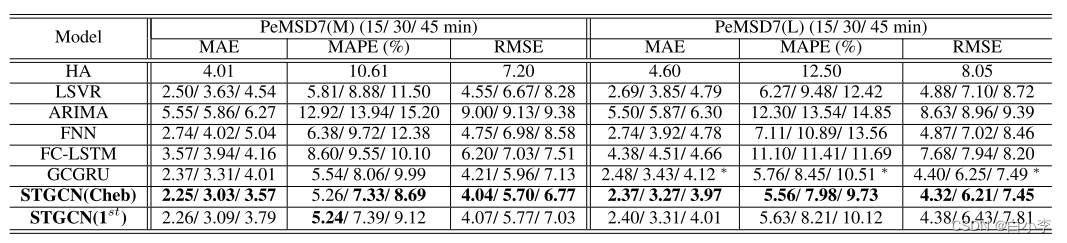
文章所提出的模型在三个评价指标中均取得了最佳的性能，且具有统计学意义(双尾t检验，α = 0.01, P < 0.01)。我们可以很容易地观察到，传统的统计和机器学习方法可能在短期预测方面表现良好，但由于错误积累、记忆问题和空间信息的缺乏，它们的长期预测并不准确。由于ARIMA模型不能处理复杂的时空数据，其性能最差。深度学习方法通常比传统的机器学习模型获得更好的预测结果。STGCN在数据集PeMSD7上的优势比BJER4更明显，因为PeMS的传感器网络更加复杂和结构化，模型可以有效地利用空间结构进行更准确的预测。

比较基于图卷积的三种方法 :GCGRU、 STGCN(Cheb) 和STGCN(1st)在早高峰和晚高峰时间的预测。

 

文章的STGCN方案比其他方法更准确地捕捉了交通高峰期的趋势;而且它能比其他车辆更早地检测到交通高峰期的结束。由于有效的图卷积和堆叠时间卷积结构，我们的模型能够快速响应交通网络的动态变化，而不像大多数循环网络那样过度依赖历史平均。

在我们的方案中，可以看到沿时间轴的卷积的好处：

 

STGCN采用默认设置。文章模型STGCN只消耗272秒，而rnn型的模型GCGRU在PeMSD7(M)上消耗3824秒。这种训练速度的14倍加速主要得益于应用时间卷积而不是循环结构。由于一阶逼近不局限于多项式的参数化，模型的优点也逐渐显现出来。与STGCN(Cheb)相比，模型STGCN(1)在更大的数据集上加速约20%，性能十分优秀。

深度学习

1、构建图数据

每个城市都相当于一个图，每一行数据都为一个节点，由于大气等数据是时序的，即每个节点按照线性关系，逐步连接下去，即一个接着一个，最后形成的图为一个线型图。每个城市都做这样的处理，广西有着14个市，即最后形成了14个图，将这些图放入一个数组中。同时根据市之间的邻近关系，将其连接起来。这就形成了我们所需要的图数据。同时按照数据以8比2的比例进行分割，形成了所需的训练数据和图数据。

 

连接关系说明：依据广西省地图对市之间进行连接，相邻的市之间，会有一条边将其连接起来；根据地图从下往上，从左往右进行连接，连接一次后则完成两个市的连接关系，例如从北海开始，与防城港、钦州、玉林连接后，当轮至防城港或钦州时不会与北海再连接一次。

连接关系：

1、 将北海与防城港、钦州、玉林连接。

2、 将防城港与钦州、崇左、南宁连接。

3、 将钦州与南宁、玉林连接。

4、 将崇左与南宁、百色连接。

5、 将南宁与贵港、来宾、河池、百色连接。

6、 将贵港与来宾、梧州连接。

7、 将梧州与贺州、来宾连接。

8、 将来宾与河池、柳州连接。

9、 将贺州与桂林连接。

10、将百色与河池相连

11、将河池与柳州相连

12、将柳州与桂林相连

2、GCN模型

图卷积网络（Graph Convolutional Network，简称 GCN）是一种用于图数据的深度学习模型，主要用于处理节点之间存在关系的数据，如社交网络、推荐系统、分子结构等。GCN 基于图结构，可以在节点上执行类似于卷积神经网络（CNN）的操作，但是适用于图数据的特殊性质。GCN 的主要思想是将节点的特征与其邻居节点的特征进行聚合，以便获取更丰富的上下文信息。通过多层的图卷积层，GCN 可以逐步地传播信息，捕捉到不同距离的节点之间的关系，从而实现节点特征的有效表征。

GCN 的核心概念和原理：

1、邻居聚合： 在每一层的图卷积中，每个节点会聚合其邻居节点的特征。这通过计算节点的邻居节点特征的加权平均来实现，权重可以使用图结构和/或特定的学习参数来确定。

2、权重共享： 类似于卷积神经网络，GCN 也使用权重共享的方式来处理不同节点。这意味着在图中的不同位置使用相同的权重参数，从而在不同节点上执行相同的特征转换操作。

3、多层堆叠： GCN 可以通过堆叠多个图卷积层来实现更强大的特征学习。在每一层，节点的特征都会被更新和改进，以便捕获更多的上下文信息。

4、图池化： 类似于 CNN 中的池化层，GCN 也可以使用图池化层来减少图的规模并提取更高级的特征。

5、非线性激活： 通常在 GCN 的每一层后会添加非线性激活函数，如 ReLU，以引入非线性变换，增强模型的表达能力。

6、节点分类和特征学习： GCN 最常见的应用是节点分类，即将节点分为不同的类别。通过训练 GCN，模型能够学习到节点的有用特征，从而实现准确的节点分类。

GCN在对于处理和预测时序性数据的优势（以大气数据为例子）

1、处理空间关系： 大气变化通常具有空间相关性，即相邻地区之间的气象数据存在相关性。GCN 可以捕捉站点之间的空间关系，通过聚合相邻站点的特征来提取空间信息，从而更准确地预测大气变化。

2、适应不规则结构： 大气站点的分布通常是不规则的，而且站点之间的连接关系可能因地理位置而异。GCN 可以适应不规则的图结构，无论站点之间的连接是怎样的，都能够有效地进行信息传播和特征学习。

3、多尺度信息： GCN 可以通过堆叠多层图卷积来捕捉不同尺度的信息。这对于预测大气变化很有用，因为不同时间尺度和空间尺度的气象变化对预测都有影响，而多层的 GCN 可以逐步地提取这些信息。

4、特征学习： 大气数据通常具有高维度的特征，而且这些特征之间的复杂关系可能不容易用传统方法捕捉。GCN 可以在多层卷积中学习特征的表征，从而更好地理解和利用这些复杂的特征。

5、迁移学习和泛化能力： GCN 可以从一个地区的数据中学习到的模式和特征迁移到其他地区，从而提高模型的泛化能力。这对于在新的地区进行大气变化预测非常有用，尤其是在数据有限的情况下。

6、数据不完整性和噪声： 大气数据可能会存在缺失值和噪声。GCN 具有一定的鲁棒性，可以在部分数据缺失或有噪声的情况下仍然有效地进行预测。

对于预测时序性数据，GCN具有其他模型所不具备的优势。

3、当前实验结果

训练的损失变化折线图：由图可以看出在模型的训练效果很好，而且收敛得很快，在200个epoch后就已经到了一个很低的值。

 

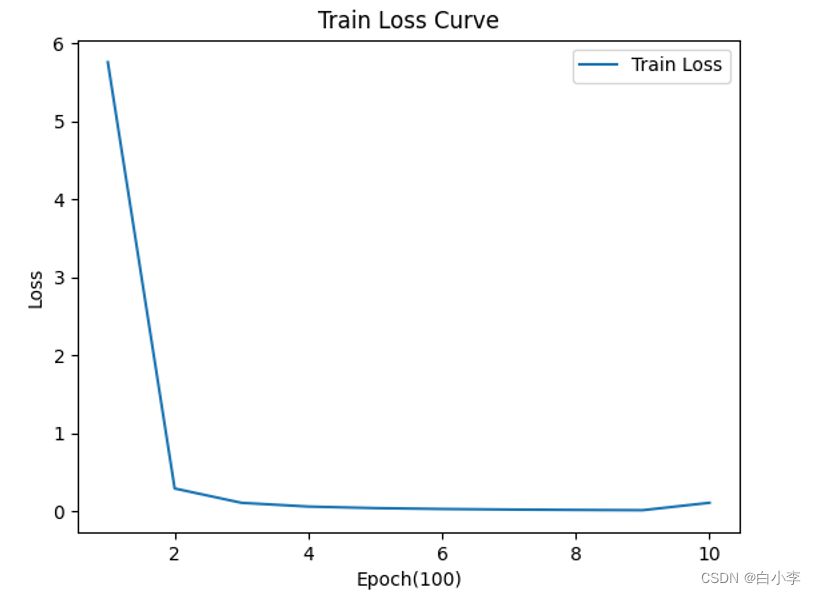
证明了模型的泛化能力很强，效果优异。

GCN主要用于处理图结构数据，能够充分利用节点之间的连接和特征信息。LSTM和GRU等时序型模型则更适用于序列数据，对于将广西各个市之间连接起来，毫无疑问这是作为图数据进行处理效果更佳。

总结

本周解决了之前不好处理时序型图数据的问题，成功构建了图数据，模型效果挺好。接下来完成项目的可视化过程。同时探究图之间的影响关系，研究模型是否能自己学习网络边权重，得多找点论文阅读沉淀下。