LeetCode 周赛上分之旅 #41 结合离散化的线性 DP 问题

⭐️ 本文已收录到 AndroidFamily，技术和职场问题，请关注公众号 [彭旭锐] 和 BaguTree Pro 知识星球提问。

学习数据结构与算法的关键在于掌握问题背后的算法思维框架，你的思考越抽象，它能覆盖的问题域就越广，理解难度也更复杂。在这个专栏里，小彭与你分享每场 LeetCode 周赛的解题报告，一起体会上分之旅。

本文是 LeetCode 上分之旅系列的第 41 篇文章，往期回顾请移步到文章末尾~

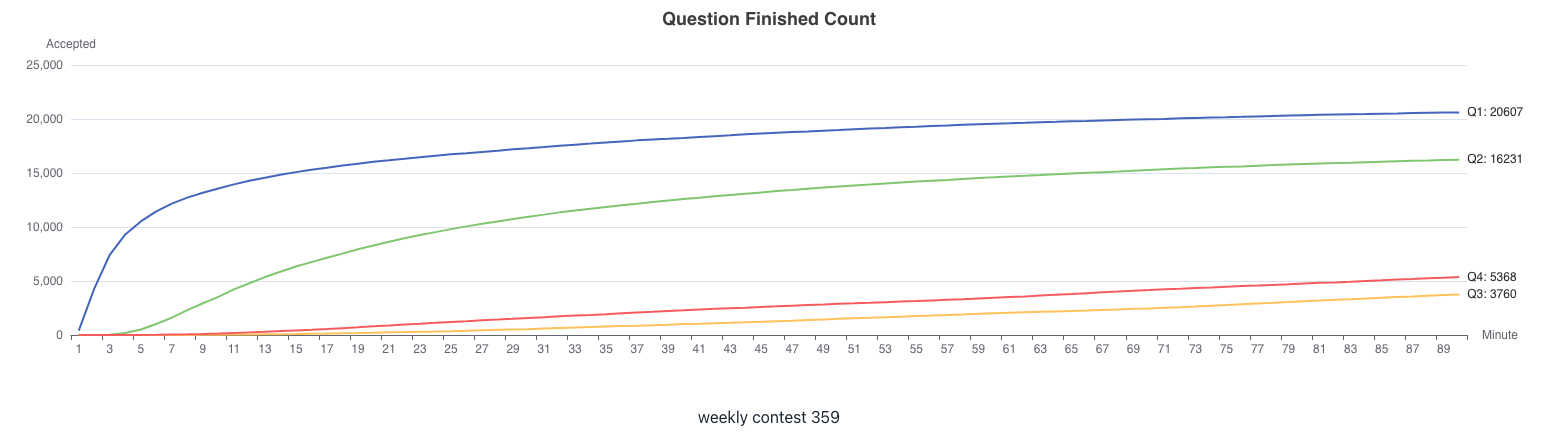
周赛 359

T1. 判别首字母缩略词（Easy）

标签：模拟、字符串

T2. k-avoiding 数组的最小总和（Medium）

标签：散列表、贪心、数学

T3. 销售利润最大化（Medium）

标签：排序、桶排序、双指针、线性 DP、离散化

T4. 找出最长等值子数组（Medium）

标签：分桶、双指针

T1. 判别首字母缩略词（Easy）

https://leetcode.cn/problems/check-if-a-string-is-an-acronym-of-words/

题解（模拟）

class Solution {
public:
    bool isAcronym(vector<string>& words, string s) {
        if (words.size() != s.length()) return false;
        for (int i = 0; i < words.size(); i++) {
            if (words[i][0] != s[i]) return false;
        }
        return true;
    }
};

复杂度分析：

时间复杂度： $O (n)$ 线性遍历；
空间复杂度： $O (1)$ 仅使用常量级别空间。

T2. k-avoiding 数组的最小总和（Medium）

https://leetcode.cn/problems/determine-the-minimum-sum-of-a-k-avoiding-array/

题解一（散列表 + 贪心）

从 1 开始从小到大枚举，如果当前元素 cur 与已选列表不冲突，则加入结果中。为了验证是否冲突，我们使用散列表在 O(1) 时间复杂度判断。

class Solution {
    fun minimumSum(n: Int, k: Int): Int {
        val set = HashSet<Int>()
        var sum = 0
        var cur = 1
        repeat(n) {
            while (!set.isEmpty() && set.contains(k - cur)) cur++
            sum += cur
            set.add(cur)
            cur++
        }
        return sum
    }
}

复杂度分析：

时间复杂度： $O (n)$ 线性遍历；
空间复杂度： $O (n)$ 散列表空间。

题解二（数学）

这道题还可以继续挖掘数学规律，我们发现当我们从 1 开始从小到大枚举时，每选择一个数的同时必然会使得另一个数 k - x 不可选。例如：

选择 1，则 k - 1 不可选；
选择 2，则 k - 2 不可选；
…
选择 k / 2，则 k - k / 2 不可选。

可以发现，最终选择的元素被分为两部分：

小于 k 的部分：选择所有和为 k 的配对中的较小值，即 1、2、3 … k / 2；
大于等于 k 的部分：与其他任意正整数相加都不会等于 k，因此大于等于 k 的数必然可以选择，即 k、k + 1、k + 2、…、k + n - m - 1共 n - m 个数。

我们令 m = min(k / 2, n)，使用求和公式可以 O(1) 求出两部分的总和：

小于 k 的部分： $m (m + 1) /2$
大于等于 k 的部分： $(n - m) * (2 * k + n - m - 1) /2$

class Solution {
    fun minimumSum(n: Int, k: Int): Int {
        val m = Math.min(n, k / 2)
        return m * (m + 1) / 2 + (n - m) * (2 * k + n - m - 1) / 2
    }
}

复杂度分析：

时间复杂度： $O (1)$
空间复杂度： $O (1)$

T3. 销售利润最大化（Medium）

https://leetcode.cn/problems/maximize-the-profit-as-the-salesman/

问题分析

对于区间 [0, n) 的房子，如果我们选择 [i, j, gold] 的 offer，那么原问题的解就变成 gold + [0, i) + (j, n) 的两个子问题的解；

定义 dp[i] 表示到 [i] 为止可以收获的最大销售利润，则对于第 [i] 间房子有卖和不卖两种选择：

不卖，那么 dp[i] = dp[i - 1]
卖，那么 dp[i] = dp[i - 1] + gold。然而题目的销售 offer 是按照区间销售而不是按照单个房子销售，如果第 i 个房子没有处于 offer 的 end 端点的话，我们是不能卖出的。

因此，我们需要找到枚举 start 端点（从后往前遍历）或枚举 end 端点（从前往后遍历）的方法，并使用转移方程 dp[i] = max(dp[i], dp[start] + gold) 更新答案。

题解一（排序 + 线性 DP + 双指针）

第一种方法，我们先对所有 offer 按照 end 端点排序，并使用 j 指针指向当前终止时间最早的 offer。在动态规划的过程中，当 i 指针与 j 指针的 end 端点重合时，可以尝试更新结果。

class Solution {
    fun maximizeTheProfit(n: Int, offers: List<List<Int>>): Int {
        val m = offers.size
        // 排序
        Collections.sort(offers) { e1, e2 ->
            e1[1] - e2[1]
        }
        var j = 0
        // 线性 DP
        val dp = IntArray(n + 1)
        for (i in 1 .. n) {
            // 不卖
            dp[i] = dp[i - 1]
            // 卖
            while (j < m && i - 1 == offers[j][1]) { // while：可能存在终点重叠的区间
                dp[i] = Math.max(dp[i], dp[offers[j][0]] + offers[j][2])
                ++j
            }
        }
        return dp[n]
    }
}

复杂度分析：

时间复杂度： $O (m l g m + n + m)$ 排序预处理时间为 $O (m l g m)$ ，动态规划时间为 $O (n + m)$ ；
空间复杂度： $O (n)$ 排序递归栈空间 + DP 数组空间。

题解二（桶排序 + 线性 DP）

第二种方法，同样是对所有 offer 按照 end 端点排序，但我们使用桶排序优化。

class Solution {
    fun maximizeTheProfit(n: Int, offers: List<List<Int>>): Int {
        // 分桶
        val buckets = Array(n) { LinkedList<IntArray>() }
        for (offer in offers) {
            buckets[offer[1]].add(intArrayOf(offer[0], offer[2]))
        }
        // 线性 DP
        val dp = IntArray(n + 1)
        for (i in 1 .. n) {
            // 不卖
            dp[i] = dp[i - 1]
            // 卖
            for (e in buckets[i - 1]) {
                dp[i] = Math.max(dp[i], dp[e[0]] + e[1])
            }
        }
        return dp[n]
    }
}

复杂度分析：

时间复杂度： $O (n + m)$ 预处理时间为 $O (n + m)$ ，其中包含 $O (n)$ 时间的数组创建时间，使用散列表可以优化预处理时间到 $O (m)$ 。动态规划中求最值部分每个 offer 最多访问 1 次整体时间，因此动态规划的时间复杂度为 $O (n + m)$ ；
空间复杂度： $O (n)$ DP 数组和分桶数组空间。

题解三（线性 DP + 离散化）

如果 n 的值域非常大的话，以上两种解法的时间和空间可能无法满足。我们发现由于影响题目的关键点仅在与 offer 的 start 端点和 end 端点，而中间空白的点或者被覆盖的点是无关紧要的。

因此，我们可以使用离散化的技巧，将所有 offer 的 start 端点和 end 端点去重后组合成新的坐标轴 points，将在 [0, n) 上的线性 DP 转换为在 [0, m) 上的线性 DP。

class Solution {
    fun maximizeTheProfit(n: Int, offers: List<List<Int>>): Int {
        // 对 start 和 end 离散化
        val pointSet = HashSet<Int>()
        for (offer in offers) {
            pointSet.add(offer[0])
            pointSet.add(offer[1])
        }
        // 排序
        val points = pointSet.toMutableList()
        points.sort()
        // 端点 -> id
        val m = points.size
        val ids = HashMap<Int, Int>()
        for (id in 0 until m) {
            ids[points[id]] = id
        }
        // 分桶
        val buckets = Array(m) { LinkedList<IntArray>() }
        for (offer in offers) {
            val start = offer[0]
            val end = offer[1]
            val gold = offer[2]
            buckets[ids[end]!!].add(intArrayOf(ids[start]!!, gold))
        }
        // 线性 DP
        val dp = IntArray(m + 1)
        for (i in 1 .. m) {
            // 不卖
            dp[i] = dp[i - 1]
            // 卖
            for (e in buckets[i - 1]) {
                dp[i] = Math.max(dp[i], dp[e[0]] + e[1])
            }
        }
        return dp[m]
    }
}

复杂度分析：

时间复杂度： $O (m l g m + m)$ 预处理时间为 $O (m l g m)$ ，瓶颈在排序，线性 DP 时间为 $O (m)$ ；
空间复杂度： $O (m)$ 离散化节点空间、分桶空间和线性 DP 空间都是 $O (m)$ 时间复杂度。

相似题目：

1235. 规划兼职工作
1751. 最多可以参加的会议数目 II
2008. 出租车的最大盈利
2054. 两个最好的不重叠活动

T4. 找出最长等值子数组（Medium）

https://leetcode.cn/problems/find-the-longest-equal-subarray/

题解（分桶 + 同向双指针）

这道题比 T3 还稍微简单一些。

分桶： 我们知道目标子数组一定发生在元素值相等的位置，因此我们可以先把所有元素下标按元素值分桶，再使用滑动窗口来寻找分桶内删除次数不超过 k 可以构造的最大连续子数组。
滑动窗口： 使用同向双指针维护目标滑动窗口，当向右扩展窗口右端点时增加删除量 delete，如果 delete 大于 k 则需要缩小左端点，过程中记录连续相等子数组的最大长度。

class Solution {
    fun longestEqualSubarray(nums: List<Int>, k: Int): Int {
        val n = nums.size
        // 分桶
        val buckets = Array(n + 1) { ArrayList<Int>() }
        for ((i, num) in nums.withIndex()) {
            buckets[num].add(i)
        }
        // 同向双指针
        var ret = 1
        for (bucket in buckets) {
            val m = bucket.size
            var delete = 0
            var i = 0
            for (j in 1 until m) {
                // 增加删除量
                delete += bucket[j] - bucket[j - 1] - 1
                while (delete > k) {
                    // 恢复删除量
                    delete -= bucket[i + 1] - bucket[i] - 1
                    // 收缩左指针
                    i++
                }
                ret = Math.max(ret, j - i + 1)
            }
        }
        return ret
    }
}

复杂度分析：

时间复杂度： $O (n)$ 分桶时间为 $O (n)$ ，所有分桶的同向双指针时间总和为 $O (n)$ ；
空间复杂度： $O (n)$ 分桶空间。

推荐阅读

LeetCode 上分之旅系列往期回顾：

LeetCode 单周赛第 358 场 · 结合中心扩展的单调栈贪心问题
LeetCode 单周赛第 357 场 · 多源 BFS 与连通性问题
LeetCode 双周赛第 111 场 · 按部就班地解决动态规划问题
LeetCode 双周赛第 110 场 · 结合排序不等式的动态规划