问题描述
由Dijkstra提出并解决的哲学家就餐问题是典型的同步问题。该问题描述的是五个哲学家共用一张圆桌，分别坐在周围的五张椅子上，在圆桌上有五个碗和五只筷子，他们的生活方式是交替的进行思考和进餐。平时，一个哲学家进行思考，饥饿时便试图取用其左右最靠近他的筷子，只有在他拿到两只筷子时才能进餐。进餐完毕，放下筷子继续思考。
如下图所示：
## 问题分析
-
关系分析
在此处，筷子是互斥的信号量，在同一时间只能由一双筷子被使用。
此外，每位哲学家只有在手上有一双筷子(两只)才能进餐，因为这筷子不是简单的单一信号量，而是应该用数组新式表现出来。 -
信号量设置
设置chopsticks为筷子的互斥信号量,用chopsticks[i]表示左手边的筷子，chopsticks[(i+1)%5]表示右手边的筷子。
假设代码如下，那么会发生什么问题呢？
semaphore chopsticks[5]={1,1,1,1,1};
Pi(){//Pi表示是第i个哲学家的进程，因为每个哲学家进程都实现同样的操作，因此不变化。
//thinking
P(chopsticks[i]);
P(chopsticks[(i+1)%5]);
//eating
V(chopsticks[i])
V(chopsticks[(i+1)%5]);
}
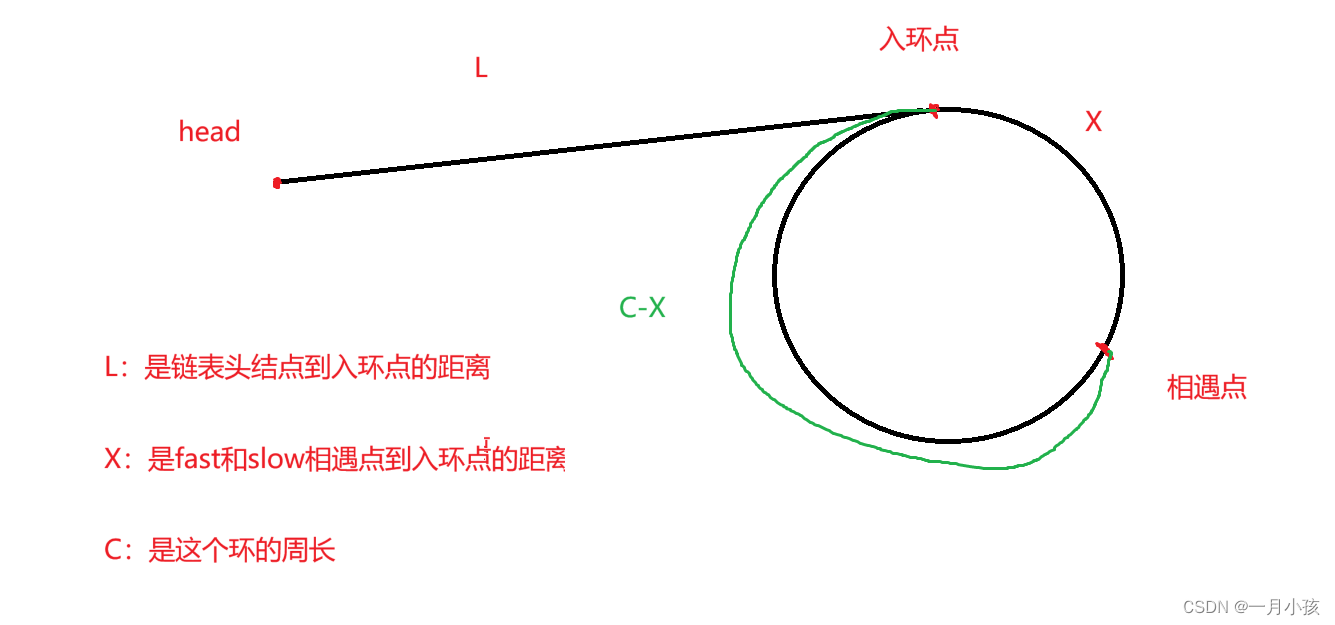
假设当第一位哲学家执行完P(chopsticks[i]);，也就是拿起一只筷子后，切换到了第二位哲学家的进程，而他也在执行了同样的操作后切换到了第三个哲学家，以此类推。就会变成下图的情况：
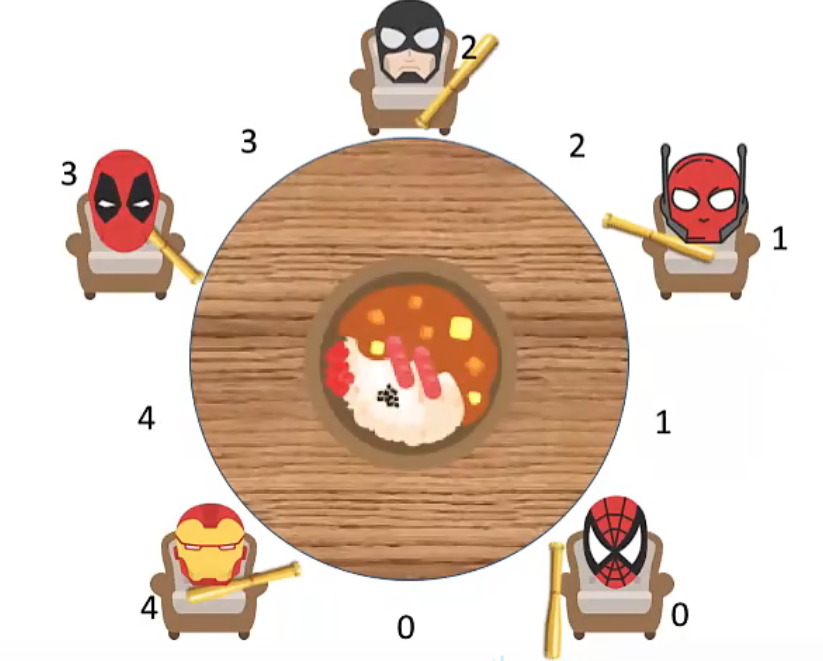
每个人手里都拿着一只筷子，但于此同时又都在等待其他人手里的筷子，最终这种循环等待的情况会造成死锁(此处不展开讨论死锁)。
那么大致的解决方案有三种：
- 保证至少有一位哲学家手中有一双筷子(两只)，可以进行就餐并就餐完毕后释放资源
- 保证最多只有四位哲学家争夺筷子，不存在五个人，从而保证了必定有一只筷子是空闲的，也就一定会有人能够就餐。
- 按照哲学家编号分为奇偶筷子，最终会使得至少有一个哲学家有一双筷子
方案一
额外设置一个信号量mutex，用来保证至少有一位哲学家手中有一双筷子(两只)。
//保证至少有一个哲学家左右手都有筷子
semaphore chopsticks[5]={1,1,1,1,1};
semaphore mutex=1;
Pi(){
//thinking
P(mutex);
P(chopsticks[i]);
P(chopsticks[(i+1)%5]);
V(mutex);
//eating
V(chopsticks[i])
V(chopsticks[(i+1)%5]);
}
方案二
额外设置一个信号量limit，通过设置该信号量初值来保证只有四位哲学家争夺筷子。
//每次只允许四个哲学家进餐
semaphore chopsticks[5]={1,1,1,1,1};
semaphore limit=4;
Pi(){
//thinking
P(limit);
P(chopsticks[i]);
P(chopsticks[(i+1)%5]);
//eating
V(chopsticks[i])
V(chopsticks[(i+1)%5]);
V(limit);
}
方案三
判断序号，如果是偶数序号的人先右后左，如果是奇数则先左后右。
semaphore chopsticks[5]={1,1,1,1,1};
Pi(){
if(i%2==0){//如果是偶数
P(chopsticks[(i+1)%5]);
P(chopsticks[i]);
//eating
V(chopsticks[(i+1)%5]);
V(chopsticks[i]);
}
else{//如果是奇数
P(chopsticks[i]);
P(chopsticks[(i+1)%5]);
//eating
V(chopsticks[i]);
V(chopsticks[(i+1)%5]);
}
}
