今日主要总结一下动态规划的一道题目，123. 买卖股票的最佳时机 III

题目：123. 买卖股票的最佳时机 III

Leetcode题目地址
题目描述：
给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入：prices = [3,3,5,0,0,3,1,4]
输出：6
解释：在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。
随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这个情况下, 没有交易完成, 所以最大利润为 0。
示例 4：

输入：prices = [1]
输出：0

提示：

1 <= prices.length <= 105
0 <= prices[i] <= 105

本题重难点

这道题目相对一文搞懂动态规划之121. 买卖股票的最佳时机问题和一文搞懂动态规划之122. 买卖股票的最佳时机 II问题难了不少。

关键在于至多买卖两次，这意味着可以买卖一次，可以买卖两次，也可以不买卖。

接来下我用动态规划五部曲详细分析一下：

1. 确定dp数组以及下标的含义
   一天一共就有五个状态，
   a. 没有操作
   b. 第一次买入
   c. 第一次卖出
   d. 第二次买入
   e. 第二次卖出
   dp[i][j]中 i表示第i天，j为 [0 - 4] 五个状态，dp[i][j]表示第i天状态j所剩最大现金。

2. 确定递推公式
   需要注意：dp[i][1]，表示的是第i天，买入股票的状态，并不是说一定要第i天买入股票，这是很多同学容易陷入的误区。
   达到dp[i][1]状态，有两个具体操作：
   操作一：第i天买入股票了，那么dp[i][1] = dp[i-1][0] - prices[i]
   操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][1] = dp[i - 1][1]
   那么dp[i][1]究竟选 dp[i-1][0] - prices[i]，还是dp[i - 1][1]呢？
   一定是选最大的，所以 dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][1]);
   同理dp[i][2]也有两个操作：
   操作一：第i天卖出股票了，那么dp[i][2] = dp[i - 1][1] + prices[i]
   操作二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i][2] = dp[i - 1][2]
   所以dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])
   同理可推出剩下状态部分：
   dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
   dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);

3. dp数组如何初始化
   第0天没有操作，这个最容易想到，就是0，即：dp[0][0] = 0;
   第0天做第一次买入的操作，dp[0][1] = -prices[0];
   第0天做第一次卖出的操作，这个初始值应该是多少呢？
   首先卖出的操作一定是收获利润，整个股票买卖最差情况也就是没有盈利即全程无操作现金为0，
   从递推公式中可以看出每次是取最大值，那么既然是收获利润如果比0还小了就没有必要收获这个利润了。
   所以dp[0][2] = 0;
   第0天第二次买入操作，初始值应该是多少呢？应该不少同学疑惑，第一次还没买入呢，怎么初始化第二次买入呢？
   第二次买入依赖于第一次卖出的状态，其实相当于第0天第一次买入了，第一次卖出了，然后在买入一次（第二次买入），那么现在手头上没有现金，只要买入，现金就做相应的减少。
   所以第二次买入操作，初始化为：dp[0][3] = -prices[0];
   同理第二次卖出初始化dp[0][4] = 0;

4. 确定遍历顺序
   从递归公式其实已经可以看出，一定是从前向后遍历，因为dp[i]，依靠dp[i - 1]的数值。

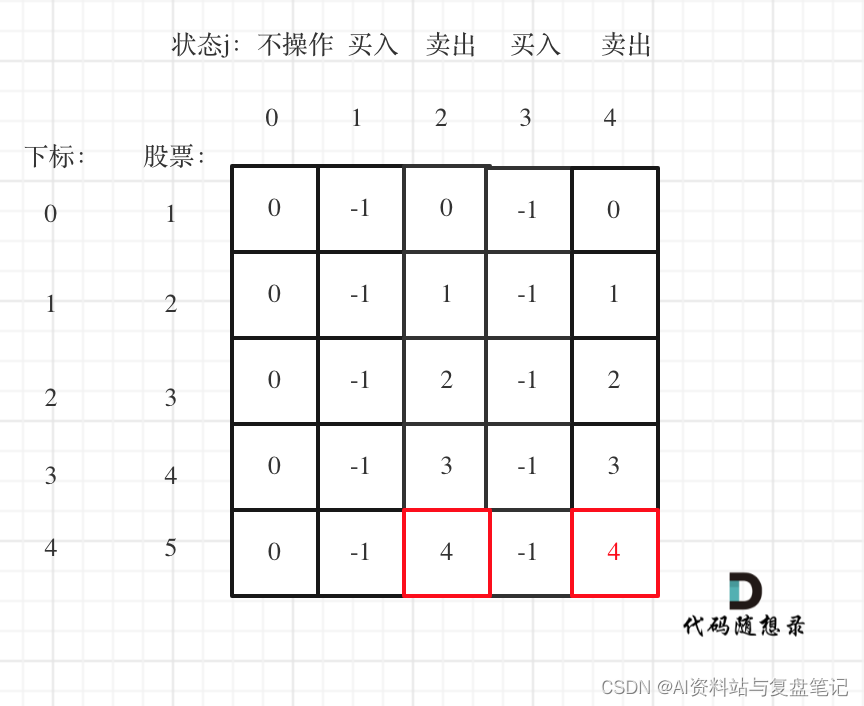
5. 举例推导dp数组

以输入[1,2,3,4,5]为例

方法一、 动态规划未优化代码

C++代码

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.size() == 0) return 0;
        vector<vector<int>>dp(prices.size(), vector<int>(5, 0));
        dp[0][1] = - prices[0];
        dp[0][3] = - prices[0];
        for(int i = 1; i < prices.size(); i++){
            dp[i][0] = dp[i - 1][0];
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
        }
        return dp[prices.size() - 1][4];
    }
};

方法二、 动态规划优化代码

其实仔细分析可以发现这五个状态其实可以简化成四种状态，因为第一种状态一直不操作其实资金一直是0，即dp[i][0]和dp[i - 1][0]一直等于0可以省略这一种状态不写！
从递推公式可以看出，dp[i]只是依赖于dp[i - 1]的状态。
那么我们只需要记录 当前天的dp状态和前一天的dp状态就可以了，可以使用滚动数组来节省空间，代码如下：

C++代码

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.size() == 0) return 0;
        vector<int>dp(4, 0);
        dp[0] = - prices[0];
        dp[2] = - prices[0];
        for(int i = 1; i < prices.size(); i++){
            dp[0] = max(dp[0], -prices[i]);
            dp[1] = max(dp[1], dp[0] + prices[i]);
            dp[2] = max(dp[2], dp[1] - prices[i]);
            dp[3] = max(dp[3], dp[2] + prices[i]);
        }
        return dp[3];
    }
};

大家会发现dp[2]利用的是当天的dp[1]。 但结果也是对的。

我来简单解释一下：

dp[1] = max(dp[1], dp[0] - prices[i]); 如果dp[1]取dp[1]，即保持买入股票的状态，那么 dp[2] = max(dp[2], dp[1] + prices[i]);中dp[1] + prices[i] 就是今天卖出。

如果dp[1]取dp[0] - prices[i]，今天买入股票，那么dp[2] = max(dp[2], dp[1] + prices[i]);中的dp[1] + prices[i]相当于是今天再卖出股票，一买一卖收益为0，对所得现金没有影响。相当于今天买入股票又卖出股票，等于没有操作，保持昨天卖出股票的状态了。

---

总结

动态规划
英文：Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。
动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的

对于动态规划问题，可以拆解为如下五步曲，这五步都搞清楚了，才能说把动态规划真的掌握了！

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

这篇文章主要总结了一些动态规划解决123. 买卖股票的最佳时机 III问题，依然是使用动规五部曲，做每道动态规划题目这五步都要弄清楚才能更清楚的理解题目！

在买卖股票的最佳时机问题的整个系列题目中使用贪心算法仅仅可以解决某个具体场景的问题，但是并不通用，而动态规划思想解决买卖股票的最佳时机整个系列问题是通用连续递进的，最好掌握一下，并且最后给出了使用滚动数组优化空间复杂度的代码！
欢迎大家关注本人公众号：编程复盘与思考随笔
(关注后可以免费获得本人在csdn发布的资源源码)