目录

1. 二分查找-I

2. 二维数组中的查找

3. 寻找峰值

4. 数组中的逆序对

5.  旋转数组的最小数字

6. 比较版本号

---

1. 二分查找-I

题目链接：二分查找-I_牛客题霸_牛客网 (nowcoder.com)

题目要求：

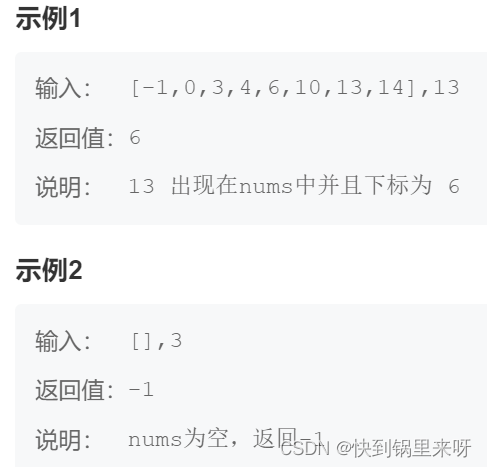
上代码

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param nums int整型一维数组 
     * @param target int整型 
     * @return int整型
     */
    public int search (int[] nums, int target) {
        int left = 0;
        int right = nums.length-1;
        while(left <= right) {
            int mid = (right+left)/2;
            if(target > nums[mid]) {
                left = mid + 1;
            }else if(target < nums[mid]) {
                right = mid - 1; 
            }else{
                return mid;
            }
        }
        return -1;
    }
}

---

2. 二维数组中的查找

题目链接：二维数组中的查找_牛客题霸_牛客网 (nowcoder.com)

题目要求：

 题目分析：

（1）暴力法

这个是我自己写的方法，就是直接暴力做的，外面一个 for 遍历行，里面一个 while 进行 每一行中的二分查找，时间复杂度是（m + logn） 空间复杂度O（1）

上代码

public class Solution {
    public boolean Find(int target, int [][] array) {
        for(int i = 0; i < array.length; i++) {
            int left = 0, right = array[0].length-1;
            while(left <= right) {
                int mid = (left + right)/2;
                if(target < array[i][mid]) {
                    right = mid - 1; 
                }else if(target > array[i][mid]) {
                    left = mid + 1;
                }else if(target == array[i][mid]){
                    return true;
                }
            }
        }
        return false;
    }
}

（2）线性查找 

然后看了一下别人的方法，主要就是从 右上角开始找，或左下角开始找

比如从 右上角开始找   ，题中说了，每行 每列 都是依次增加的 

这种方法一个while就可以，时间复杂度低 O（m+n），同理 如果从左下角开始走也一样

上代码

        public boolean Find(int target, int [][] array) {
            if(array == null || array.length == 0 || array[0].length == 0) {
                return false;
            }
            int rows = 0; //行
            int column = array[0].length - 1; //列
            while(rows < array.length && column >= 0) {
                if(array[rows][column] == target) {
                    return true;
                }else if(array[rows][column] < target) {
                    rows++;
                }else {
                    column--;
                }
            }
            return false;
    }
}

---

3. 寻找峰值

题目链接：寻找峰值_牛客题霸_牛客网 (nowcoder.com)

题目要求：

 题目分析：

（1）暴力法

题中说的是 峰值元素 是大于右边元素，和左边元素的

如果只是 根据条件，进行for循环遍历数组（注意不要数组越界的问题），发现测试用例不能全部跑过去，

出现了比如【2，9】峰值9，返回下标1；比如【9，2】峰值9，返回下标1

所以还要判断的一种情况是，

如果for循环遍历到最后，还没出现峰值，那么就是单调递增（此时判断后两个元素大小），峰值就是最后一个

如果for循环遍历到最后，还没出现峰值，那么就是单调递减（此时判断前两个元素大小），峰值就是第一个

这么写的原因是题中说 nums[-1] = nums[n] = 负无穷，也就是走到数组边界外时，是最小的

所以还要判断的一种情况就是 数组边界是不是 “峰值” 的问题

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param nums int整型一维数组 
     * @return int整型
     */
     public int findPeakElement (int[] nums) {
        int len = nums.length;
        for(int i = 1; i < len; i++) {
            if(i < len-1 && nums[i-1] < nums[i] && nums[i+1] < nums[i]) {
                return i;
            }else if(i == len - 1 && nums[0] > nums[1]) {
                return 0;
            }else if(i == len - 1 && nums[len-1] > nums[len-2]) {
                return len-1;
            }
        }
        return 0;
    }
 }

（2）二分法 

这个我看别人写的，是用 二分法做的，

找到数组中间节点mid，如果中间节点小于右边，说明峰值在右边，left就要收缩到mid+1

如果中间节点大于右边，说明峰值可能是mid自己，也可能是mid左边，right就要收缩到mid

到while 结束后，此时left 和 right 相等，随便返回谁都可以

        public int findPeakElement (int[] nums) {
            int left = 0;
            int right = nums.length - 1;
            while(left < right) {
                int mid = (left + right) / 2;
                //右边大，峰值在右 
                if(nums[mid] < nums[mid+1]) {
                    left = mid + 1;
                }else {
                    //左边大，峰值在左（也可能峰值就是自己）
                    right = mid;
                }
            }
            return right;
        }

---

4. 数组中的逆序对

题目链接：数组中的逆序对_牛客题霸_牛客网 (nowcoder.com)

题目要求：

题目分析：

题意就是,在数组中, 如果前一个数字 大于 后一个数字, 就计数+1,直到最后,就%1000000007

既然是要比较这样数组中每两个数字的大小,那就直接暴力两两比较

(1) 暴力

上代码

import java.util.*;

public class Solution {
    public int InversePairs(int [] array) {
        if(array.length == 0 || array.length == 1) {
            return 0;
        }
        int fast = 1;
        int slow = 0;
        long count = 0;
        while(slow < array.length-1) {
            if(array[slow] > array[fast]) {
                count++;
            }
            fast++;
            if(fast == array.length) {
                slow++;
                fast = slow + 1;
            }
        }
        return (int)(count%1000000007);
    }
}

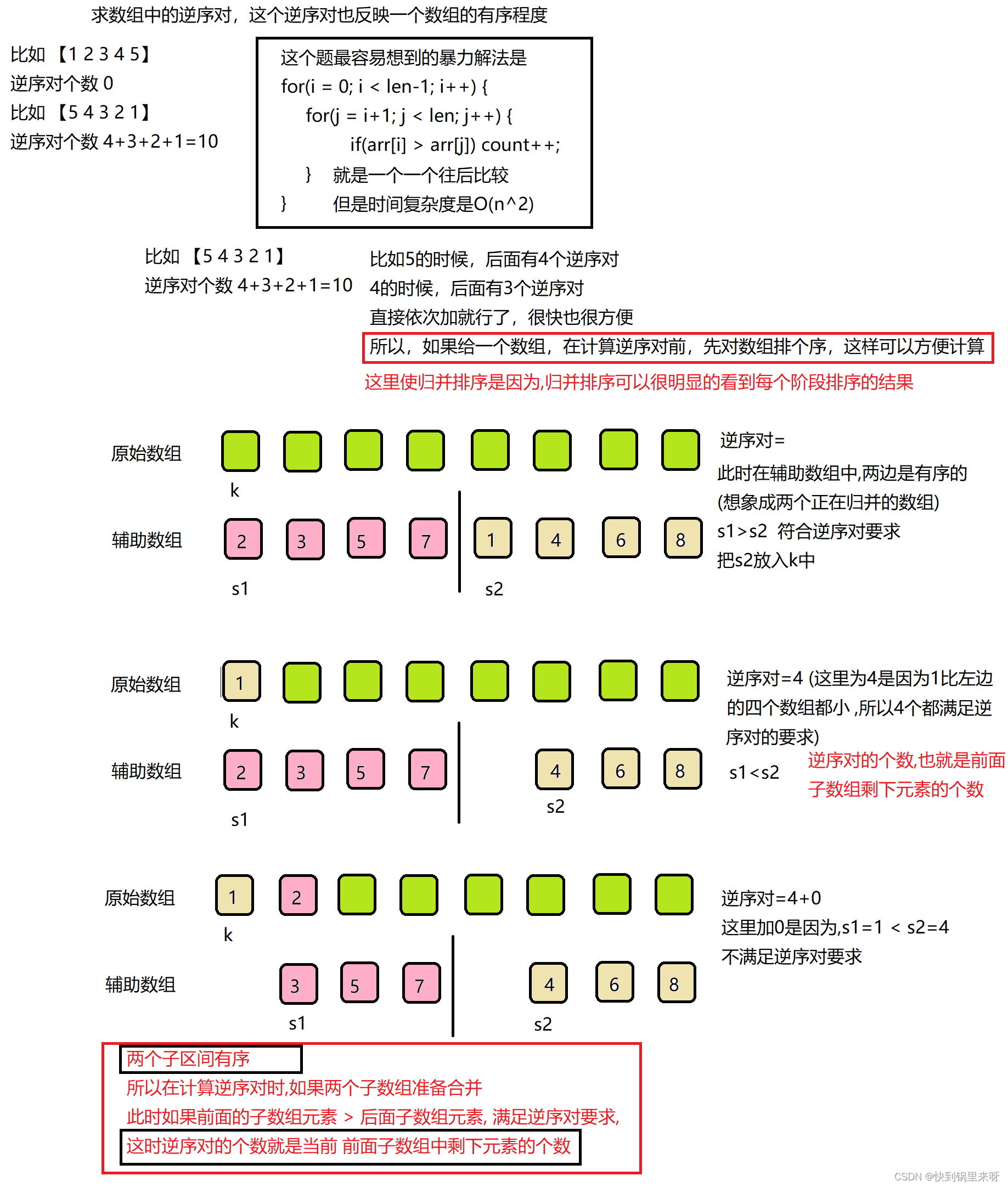
(2) 归并

因为这里的思路和归并一样,所以代码部分就是写个归并排序,然后在归并排序中进行合并比较时,前面大的时候,进行count计数(这里加的是前半部分剩余元素的个数)

具体归并代码也可以看看我这篇博客

http://t.csdn.cn/gqmuP

import java.util.*;

public class Solution {
    long count = 0;
    public int InversePairs(int [] array) {
        mergeSort(array, 0, array.length-1);
        return (int)(count%1000000007);
    }
    //分割
    private void mergeSort(int[] array, int left, int right) {
        if(left >= right) {
            return;
        }
        int mid = left + (right - left)/2;
        mergeSort(array,left,mid);
        mergeSort(array,mid+1,right);
        merge(array,left,right,mid);
    }
    private void merge(int[] array, int start, int end, int midIndex) {
        int[] tmpArr = new int[end-start+1];//辅助数组
        int k = 0;//tmpArr数组下标
        int s1 = start;
        int s2 = midIndex+1;
        while(s1 <= midIndex && s2 <= end) {
            if(array[s1] <= array[s2]) {
                tmpArr[k++] = array[s1++];
            }else {
                //多加这行代码,进行计数 
                count += (midIndex-s1+1);
                tmpArr[k++] = array[s2++];
            }
        }
        while(s1 <= midIndex) {
            tmpArr[k++] = array[s1++];
        }
        while(s2 <= end) {
            tmpArr[k++] = array[s2++];
        }
        //将排好序的辅助数组拷贝回去
        for(int i = 0; i < k; i++) {
            array[i+start] = tmpArr[i];
        }
    }
}

---

5.  旋转数组的最小数字

题目链接：旋转数组的最小数字_牛客题霸_牛客网 (nowcoder.com)

题目要求：

题目分析：

上代码

public class Solution {
    public int minNumberInRotateArray(int [] array) {
        int left = 0;
        int right = array.length-1;
        while(left < right) {
            int mid = (left + right)/2;
            //此时最小的数字在右边
            if(array[mid] > array[right]) {
                left = mid + 1;
                //无法判断在右边哪里,一个一个试
            }else if(array[mid] == array[right]) {
                right--;
            }else {
                //最小数组在左边
                right = mid;
            }
        }
        return array[left];
    }
}

6. 比较版本号

题目链接：比较版本号_牛客题霸_牛客网 (nowcoder.com)

题目要求：

 题目分析：

(1) 分割截取

可以利用split将.进行分割,转为字符串数组

因为版本号长度不一, 要进行比较的话,可以将短的版本号,后面取0 方便比较

下面就是将字符串数组中的每个字符串元素,转为整数进行比较了

上代码

import java.util.*;


public class Solution {
    public int compare (String version1, String version2) {
        String[] v1 = version1.split("\\.");
        String[] v2 = version2.split("\\.");
        for(int i = 0; i < v1.length || i < v2.length; i++) {
            //较短的版本号后面取0
            String str1 = i < v1.length ? v1[i] : "0";
            String str2 = i < v2.length ? v2[i] : "0";
            int v11 = Integer.parseInt(str1);
            int v22 = Integer.parseInt(str2);
            //比较数字大小
            if(v11 > v22) {
                return 1;
            }
            if(v11 < v22) {
                return -1;
            }
        }
        return 0;
    }
}

(2) 双指针遍历截取比较

import java.util.*;


public class Solution {
    public int compare (String version1, String version2) {
        int n1 = version1.length();
        int n2 = version2.length();
        int i = 0, j = 0;
        while(i < n1 || j < n2) {
            //截取version1的.前面的数字
            long num1 = 0;
            while(i < n1 && version1.charAt(i) != '.') {
                num1 = num1*10 + (version1.charAt(i) - '0');
                i++;
            }
            //跳过.
            i++;
            long num2 = 0;
            while(j < n2 && version2.charAt(j) != '.') {
                num2 = num2*10 + (version2.charAt(j) - '0');
                j++;
            }
            j++;
            if(num1 > num2) {
                return 1;
            }
            if(num1 < num2) {
                return -1;
            }
        }
    return 0;
    }
}