题目

我们正在玩一个猜数游戏，游戏规则如下：
我从 1 到 n 之间选择一个数字。你来猜我选了哪个数字。如果你猜到正确的数字，就会赢得游戏。如果你猜错了，那么我会告诉你，我选的数字比你的更大或者更小，并且你需要继续猜数。每当你猜了数字x并且猜错了的时候，你需要支付金额为x的现金。如果你花光了钱，就会输掉游戏。给你一个特定的数字n，返回能够确保你获胜的最小现金数，不管我选择那个数字。

示例

在这里插入图片描述

输入：n = 10
输出：16

题解

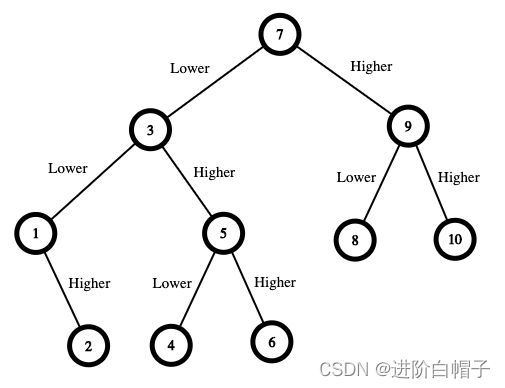
这里还是首先人工找确定一个大体的过程。以上图示例进行说明，开始的时候一共有10个可选数据。比如选择1之后只有比1大的子序列从2到10，选择2序列被分成两个。接下现是对划分后的子序列继续执行相同的操作。可见这至少是一个递归过程。递归函数的目标是给定一个可选数据列，计算获胜的最小现金数。这个递归也与最终所求的问题一致。
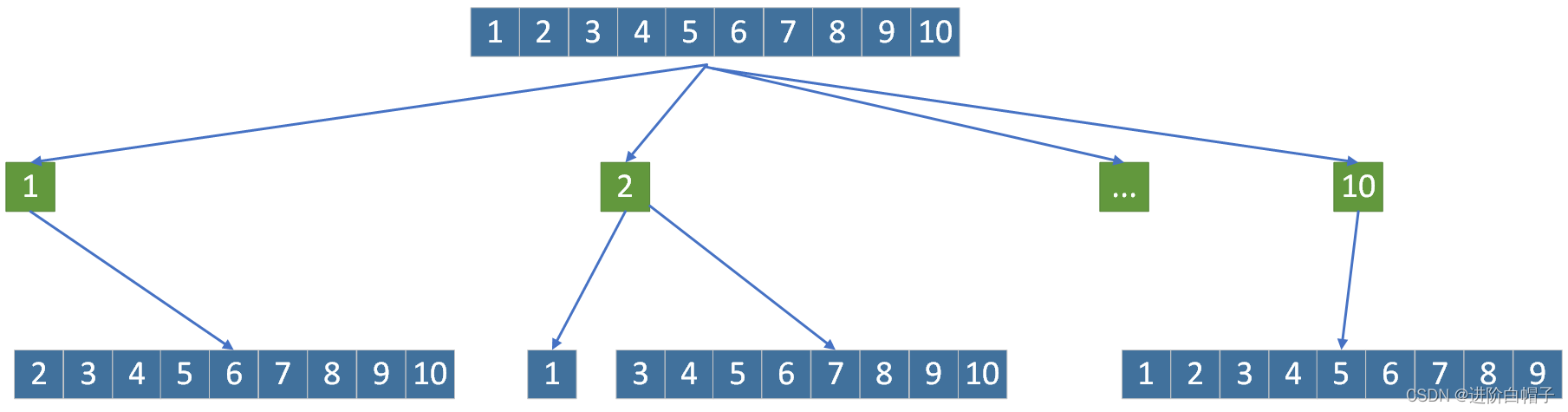
在这里插入图片描述
那么我们来分析一下这个递归函数如何写。递归函数的输入只包含了一个数据列，这个数据列明显是1到n的一个子序列，因此，需要用两个变量确定该序列start,与end。dfs(start,end)表示[start,start+1,…,end]这个数据如果获胜需要支付的最小现金数。比如初始[1,…,10]数据列，猜x获胜有3种情况：

猜对了，确实是x，那么需要支持0
猜错，正确的数据比x小，这就转化成了求[1,…,x-1]这个数据列获胜需要支付的最小现金数。支付的现金数=x+dsf(1,x-1)。
猜错，正确的数据比x大，这就转化成了求[x+1,…,n]这个数据列获胜需要支付的最小现金数。支付的现金数=x+dsf(x+1,n)。
因此，要想获得胜利的话，需要取这三种情况的最大值。对于猜x中的x可以是从1到n的所有数。而x所有的可选择的数中需要选择最小的一个即可以得到获胜需要支付的最小现金数。
递归方程可以写为：

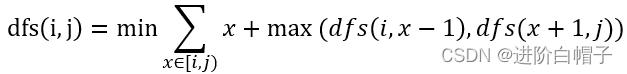
最后，这道题目的边界有些特殊。
1 i=j表示最后剩下一下数了，那一定能猜对，因此不需要支持现金所以为0；
2 i=j-1，这种情况表示只剩下两个数，这里有两种选择。选择i的话，选对了不需要支持现金，选错了需要支持i。选择j的话选对了支持0,选错了支付j。这两种选择支个最小值，因此是i。
到这里递归函数的整个过程就比较明显了。

递归函数：

输入：数据列表
输出：获胜的最小支付现金数
过程：边界条件判定，递归过程。

代码

class Solution:
    def getMoneyAmount(self, n: int) -> int:
        #记忆化搜索
        @functools.lru_cache(maxsize=None)
        def dfs(start, end) :
            #边界条件
            if end-start <= 0 : return 0
            if end-start == 1 : return l
            #递归方程
            return min((i+max(sol(l,i-1), sol(i+1,r)) for i in range(l, r+1)))
        return sol(1,n)

整个过程还是比较简单的。比较好想到的。

动态规划

通常情况记忆化搜索+递归在能固定状态维度的情况下都能写成动态规划。但是这里相对需要注意的是动态规划状态方程的遍历顺序。
这里动态规划dp[i][j]表示的含义与前面的递归函数dfs是一样的，表示从i到j的数据列中想要获胜的最小支付现金数。这个根据前面的分析写下状态转移方程：
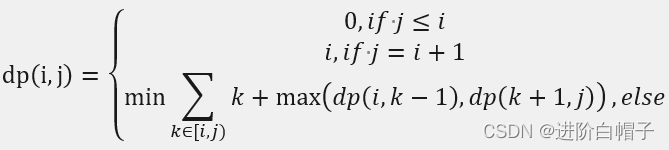
在这里插入图片描述
这里稍微有点绕人的地方就是边界问题。首先是j=i+1的情况需要确定。其次，遍历的时候k不能等于j，如果等于j的话就超出边界了。
首先，初始化dp状态矩阵如下图。

下面根据状态转移矩阵来尝试更新一下dp矩阵，先从左到右，从上到下更新。
第一步更新dp[1][1]。
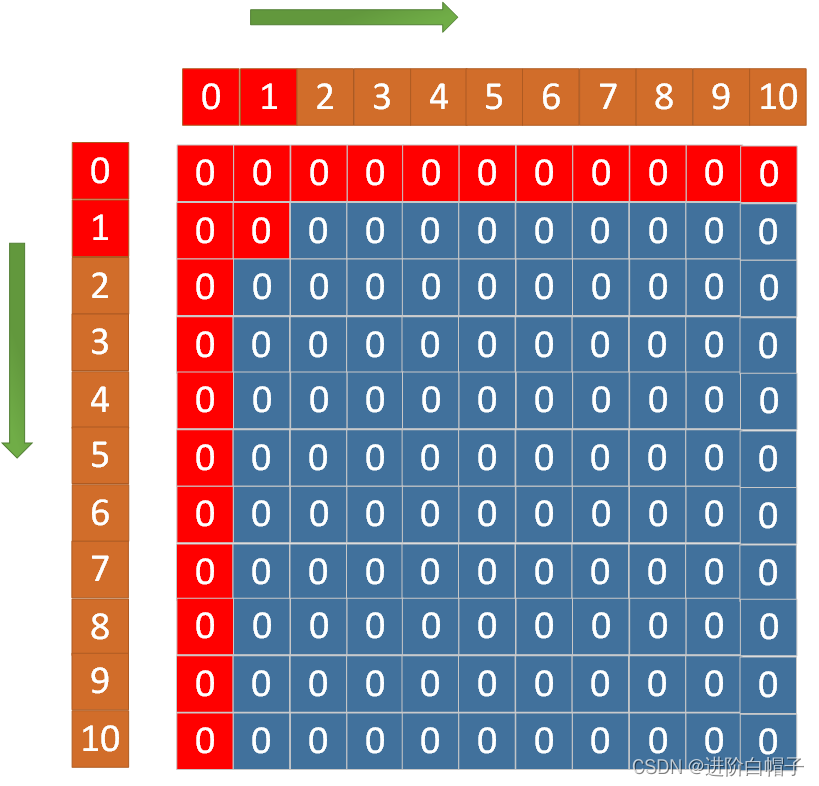
在这里插入图片描述
第2步更新dp[1][2]。dp[1][2]不依赖于其他状态，直接根据j=i+1来更新。

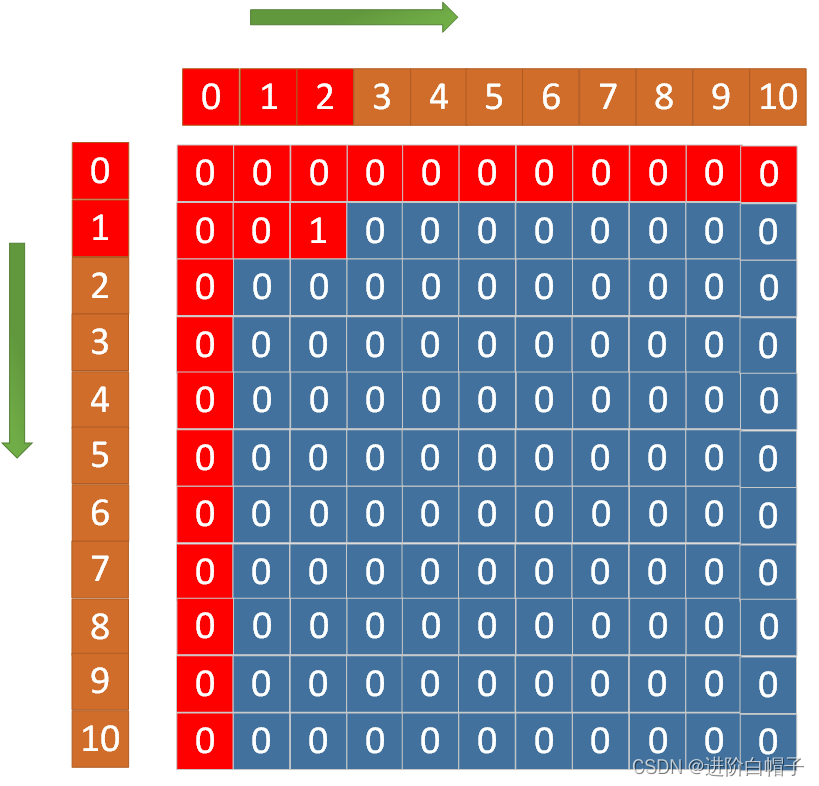
接下来是关键更新dp[1][3]，这里dp[1][3]根据公式依赖于dp[1][0],dp[1][3]，dp[1][1],dp[2][3]。但是dp[2][3]现在是一个未更新状态。因此这遍历过程是从左到右，从下往上。
现在就可以写代码了。

递归代码：

class Solution:
    def getMoneyAmount(self, n: int) -> int:
        #特殊情况
        if n==1:
            return 0
        #dp初始化
        dp=[[0]*(n+1) for _ in range(n+1) ]
        #i从下往上 j从左到右
        for i in range(n-1,0,-1):
            for j in range(i+1,n+1):
                #状态转移方程中的j=i+1的情况
                if j-i==1:
                    dp[i][j]=i
                else:
                    #状态转移方程
                    dp[i][j]=min([k+max(dp[i][k-1],dp[k+1][j]) for k in range(i,j)])
        return dp[1][n]

计算复杂性

时间复杂度： $O(n^3)$ ，其中 n 是给输入的参数。为什么是 $n^3$ ，可以看到代码中有i与j的两层for循环遍历最坏是 $n^2$ 。但是在状态转移方程中也存在一个关于k的for循环遍历。因此。时间复杂度是 $O(n^3)$ 。
空间复杂度： $O(n^2)$ ，是dp状态矩阵占用的空间。