OK，今天来讲一讲线段树~~

线段树是什么

线段树（$Segment$$Tree$）是一种二叉树，用于区间查询。线段树的每个节点表示一个区间，根节点表示整个区间，子节点表示区间的一半。线段树的典型应用是解决区间查询问题，例如区间最大值、区间最小值等。

线段树的实现

线段树的构建过程可以通过递归实现。给定一个数组$arr$，线段树的根节点表示$arr[0]$到$arr[n-1]$之间的区间和（或其他区间操作）。根节点的左子节点表示$arr[0]$到$arr[(n-1)/2]$之间的区间和，右子节点表示$arr[(n-1)/2+1]$到$arr[n-1]$之间的区间和。依次类推，直到区间被划分为长度为1的节点。

线段树的每个节点都会记录该节点表示的区间的一些统计信息，例如区间和、区间最大值、区间最小值等。该统计信息可以通过节点的左子节点和右子节点的统计信息来计算得到。

当要查询的区间与当前节点表示的区间有重叠时，查询操作会继续向下递归。当要查询的区间与当前节点表示的区间完全相等时，查询操作可以直接返回当前节点的统计信息。当要查询的区间在当前节点表示的区间的左半部分时，查询操作会向左子节点递归。当要查询的区间在当前节点表示的区间的右半部分时，查询操作会向右子节点递归。

当要更新的位置在当前节点表示的区间内时，更新操作会继续向下递归。当更新到叶子节点时，将该位置的值更新为给定的新值。然后，更新操作会向上递归，将更新后的值传递给父节点并重新计算父节点的统计信息。

线段树的时间复杂度

线段树的时间复杂度为$O(log(n))$，其中n为数组的长度。这是因为构建线段树需要对每个节点进行一次操作，总共需要$O(n)$的时间。查询操作的时间复杂度为$O(log(n))$，因为查询的过程类似于二分查找，每次将查询范围缩小一半，最多需要递归$log(n)$次。更新操作的时间复杂度也为$O(log(n))$。

线段树是一种非常强大的数据结构，可以用于解决各种区间查询问题。然而，线段树的应用并不局限于时间复杂度为$O(log(n))$的问题，它还可以结合其他数据结构和算法来实现更高效的解决方案。例如，线段树可以与离散化、树状数组等结合使用，用于解决动态区间查询问题。同时，线段树还可以用于解决一些特殊情况下的区间查询问题，例如动态维护滑动窗口中的最大值、最小值等。

线段树的应用

线段树的应用非常广泛，以下是一些常见的应用场景：

• 区间最小值/最大值查询：通过线段树可以在$O(log(n))$的时间内找到任意区间的最小值或最大值。这在处理动态数据的情况下非常有用，例如动态维护滑动窗口的最小值、最大值。

• 区间和查询：线段树可以用来快速计算区间内所有元素的和。这在求解数组范围内的连续子数组和、处理区间加法或区间更新操作等问题非常有用。

• 区间更新：线段树可以将区间内的某个值更新为新值。这在处理动态修改数据的情况下非常有用，例如修改数组某个位置的值，或者将区间内的所有元素增加某个固定值。

• 区间统计：除了求和、最小值、最大值等基本操作外，线段树还可以做更复杂的区间统计操作。例如，可以通过线段树求解区间内的第$k$小元素，或者统计区间内有多少个不同的元素等。

• 离散化：离散化是一种将连续的数据映射到离散的区间中的方法。通过使用线段树可以很方便地实现离散化操作，将大量的连续数据映射到有限的离散区间内，从而减小数据规模，提高查询效率。

• 区间交集查询：线段树可以用于判断两个区间是否有交集，以及计算出两个区间的交集。这在处理区间重叠问题、查找共同区间等场景下非常有用。

• 区间覆盖查询：线段树可以用于快速查找某个区间是否完全被覆盖，以及计算出所有覆盖某个区间的区间。这在处理区间合并、区间分割等问题非常有用。

线段树是一种非常强大而灵活的数据结构，可以根据需求进行扩展和优化。通过合理地设计数据结构和算法，线段树可以高效地解决各种区间查询问题，提高程序的性能和可扩展性。

线段树的节点结构

线段树的节点结构一般包含以下几个属性：

start 和 end：表示当前节点所代表的区间的起始和结束位置。
一个外挂：依题目而定

其他操作和优化

线段树还可以进行一些其他的操作和优化，例如：

• 惰性更新：使用标记来延迟更新，减少更新操作的次数，提高效率。
• 区间增量：维护区间值的增量，而不是直接修改区间的值，可以减少更新操作的次数。
• 动态修改：支持在原始数据的基础上进行修改，而不需要重新构建整个线段树。

例题——影子宽度

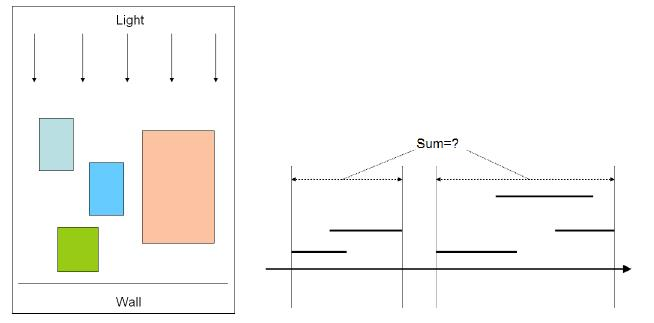
精灵王的桌子上零散地放着若干个盒子，桌子的后方是一堵墙。如下图所示。现在从桌子的前方射来一束平行光，把盒子的影子投射到了墙上。问影子的总宽度是多少？

输入输出格式

输入格式

• 第1行：盒子的个数N（1≤=N≤10000）。
• 第2…N+1行：每个盒子的起始位置S和结束位置T（1≤S, T≤100000）。

输出格式

• 第1行：包含一个整数，表示影子的总宽度。

输入输出样例

输入样例

4
1 2
3 5
4 6
5 6

输出样例

4

例题讲解

这题纯纯版题呀！！

#include <bits/stdc++.h>
using namespace std;
const int N=120000;
int n,m,maxx,minn,a[N],b[N],cover[4*N];
void insert(int idx,int ll,int rr,int x,int y) {
	if (x<=ll && y>=rr)		//如果区间范围包含当前线段
		cover[idx]=1;
	if(cover[idx]==1)	//如果当前线段已经被标记了
		return;
	int mid=(ll+rr)/2;
	if (y<=mid)
		insert(idx*2,ll,mid,x,y);	//左子树递归
	else if (x>=mid)
		insert(idx*2+1,mid,rr,x,y);		//右子树递归
	else {		//拆分成两边，分别递归
		insert(idx*2,ll,mid,x,y);
		insert(idx*2+1,mid,rr,x,y);
	}
}
int count(int idx,int ll,int rr,int x,int y) {
	if (cover[idx]==1)		//如果当前线段被标记
		return rr-ll;		//返回长度
	if (rr-ll>1) {		//如果当前线段还是一个线段
		int mid=(ll+rr)/2;
		int tx=count(idx*2,ll,mid,x,y);
		int ty=count(idx*2+1,mid,rr,x,y);
		return tx+ty;
	}
	return 0;
}
int main() {
	scanf ("%d",&n);
	for (int i=1;i<=n;i++) {
		scanf("%d%d",&a[i],&b[i]);
		if (a[i]>maxx)
			maxx=a[i];
		if (a[i]<minn)
			minn=a[i];
		if (b[i]>maxx)
			maxx=b[i];
		if (b[i]<minn)
			minn=b[i];
		//一堆判断，求最大边界和最小边界
		//有时候 是输入的数
	}
	for (int i=1;i<=n;i++)
		insert(1,minn,maxx,a[i],b[i]);		//标记线段
	printf("%d",count(1,minn,maxx,minn,maxx));		//输出结果
	return 0;
}