💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

电力系统中的环境经济调度问题是指在电力系统运行过程中，考虑到环境保护和经济效益的情况下，对发电机组的出力进行调度，以实现系统的可靠运行和最小的经济成本。

MOEA/D（Multi-Objective Evolutionary Algorithm based on Decomposition）是一种多目标优化算法，通过将多目标问题分解为一系列单目标子问题，并使用进化算法求解这些子问题，最终得到全局最优解的近似集合。

在基于MOEA/D求解电力系统中的环境经济调度问题的研究中，可以将环境保护和经济效益作为两个目标函数。环境保护目标可以通过减少发电机组的排放量来实现，例如减少二氧化碳、氮氧化物和颗粒物等污染物的排放量。经济效益目标可以通过降低发电成本来实现，例如减少燃料成本和运行维护成本等。

具体而言，可以将电力系统中的环境经济调度问题建模为一个多目标优化问题，其中目标函数包括最小化发电成本和最小化污染物排放量。约束条件包括电力系统的供需平衡、各发电机组的出力范围限制、发电机组的启停次数限制等。

然后，可以使用MOEA/D算法对该多目标优化问题进行求解。首先，将多目标问题分解为一系列单目标子问题，每个子问题都是一个单目标优化问题，例如最小化发电成本或最小化污染物排放量。然后，使用进化算法对每个子问题进行求解，得到一组近似最优解。最后，通过比较和选择这些近似最优解，得到全局最优解的近似集合。

通过基于MOEA/D的方法求解电力系统中的环境经济调度问题，可以同时考虑环境保护和经济效益的因素，得到一组最优的发电机组出力方案，以实现电力系统的可靠运行和最小的经济成本。这对于提高电力系统的可持续发展和环境保护具有重要意义。

📚2 运行结果

 

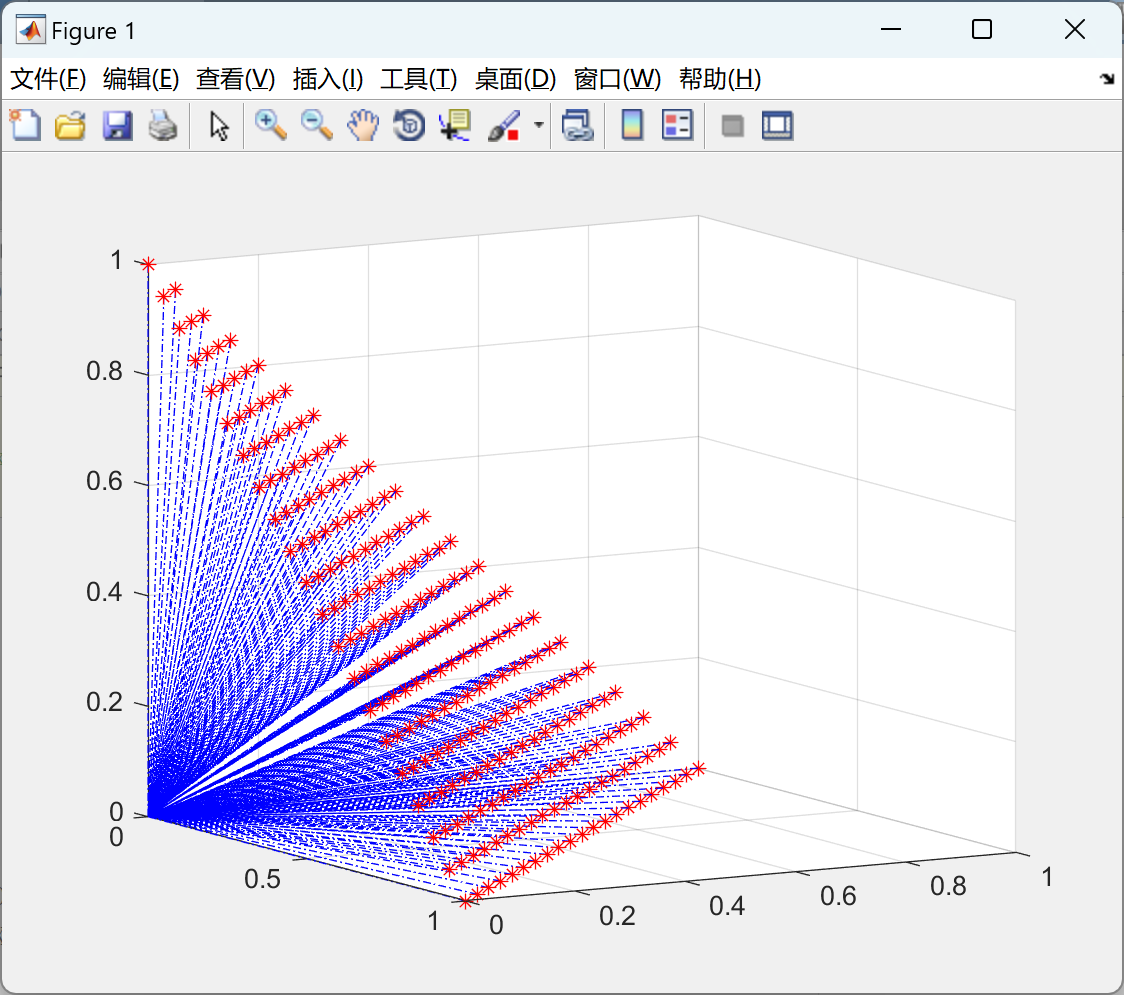
 部分代码：

function demo()    
addpath('..');  % the major genetic operators are located in the parent directory
clear all;
clc;
close all;

format long
mop = testmop('zdt1',30);

pareto = moead( mop, 'popsize', 100, 'niche', 20, 'iteration', 200, 'method', 'te');

% pareto = moead( mop, 'popsize', 100, 'niche', 20, 'iteration', 200, 'method', 'ws');

end

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]朱永胜,王杰.采用MOEA/D算法的含风电系统环境经济调度[J].郑州大学学报：工学版, 2014(4):5.DOI:10.3969/j.issn.1671-6833.2014.04.023.

[2]罗顺根,郭秀萍.用改进的MOEA/D算法求解微电网电力调度多目标优化问题[J].系统科学与数学, 2020, 40(1):24.DOI:CNKI:SUN:STYS.0.2020-01-006.

[3]李鹏波.基于多目标优化的含风电场电力系统环境经济调度研究[D].山东大学,2015.DOI:10.7666/d.Y2792777.

🌈4 Matlab代码实现