漫谈红黑树:红黑树的奇妙演化
- 一、红黑树的提出
- 二、红黑树性质的简单推导
- 三、结论
博主简介
💡一个热爱分享高性能服务器后台开发知识的博主,目标是通过理论与代码实践的结合,让世界上看似难以掌握的技术变得易于理解与掌握。技能涵盖了多个领域,包括C/C++、Linux、Nginx、MySQL、Redis、fastdfs、kafka、Docker、TCP/IP、协程、DPDK等。
👉
🎖️ CSDN实力新星、CSDN博客专家、华为云云享专家、阿里云专家博主
👉
一、红黑树的提出
追溯起来的话,红黑树的启蒙最早应该是由计算机科学家 Rudolf Bayer 和 Volker Weber 在 1972 年的一篇论文《Maintaining a Search Tree Under Dynamic Insertions and Deletions》引出的;他们的论文主要关注在外部存储器上维护平衡的二叉搜索树,用于数据库的索引结构。
但是,真正的红黑树数据结构应该是Leo J. Guibas和Robert Sedgewick在1978年发布的一篇《A dichromatic framework for balanced trees》论文提出的,该论文提出了一个用于平衡树算法实现和研究的统一框架。该框架只调用包含两个节点的二叉树,它允许每个节点有一个比特,称为节点的颜色来存储平衡信息。也就是红色和黑色。

这篇论文的作者讨论了与AVL树使用的单旋转和双旋转相同的方式改变树的结构。只是区别在于何时决定旋转和操作节点的颜色。
论文的第一部分主要介绍了常见的平衡树算法可以在O(logN)的时间复杂度内执行各种操作。然而,由于平衡树的种类繁多且缺乏性能分析结果,实际实现起来往往很麻烦。为了解决这个问题,作者提出了一个统一的框架,用于实现和研究平衡树算法。该框架仅处理包含两种类型节点(内部节点和外部节点)的二叉树,并使用每个节点的颜色来存储平衡信息。
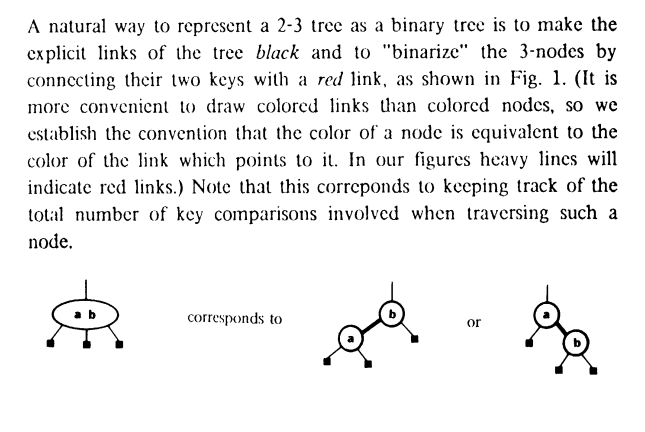
在这里作者观察到了一些特性:
- 用红色和黑色来储存平衡信息。也就是红黑树的性质之一:节点是红色或黑色。
- 路径上的黑弧数将是相同的。也就是红黑树的性质之一:从任一节点到其每个叶子节点的简单路径上,所有黑色节点的数量相等。
- 在任何路径上都不会出现两个连续的红色链接。也是红黑树的性质之一:红色节点的子节点必须是黑色,不能有两个连续的红色节点。
- 外节点为黑色,内部节点可能是红色或黑色。也是红黑树的性质之一:叶子节点(NIL节点)是黑色。

作者还发现,每个AVL树都可以变为一棵2-3-4树:在二色表示法中,这可以非常简洁地描述。将节点的高度定义为从该节点到外部节点的最长路径的长度。要将一棵AVL树变成2-3-4树,只需将那些从偶数高度的节点到 奇数高度的节点的链接涂成红色即可。
第二部分使用二色框架进行平衡树算法分析。作者通过设计一个基于局部上下文的平衡器,实现了在不收集整个树的信息的情况下进行平衡操作。经过他们的仿真研究和实证观察,发现各种算法在平均情况下表现良好,并且对输入数据的敏感性较低。而且代码更简洁,只需要传统AVL代码的60%左右。
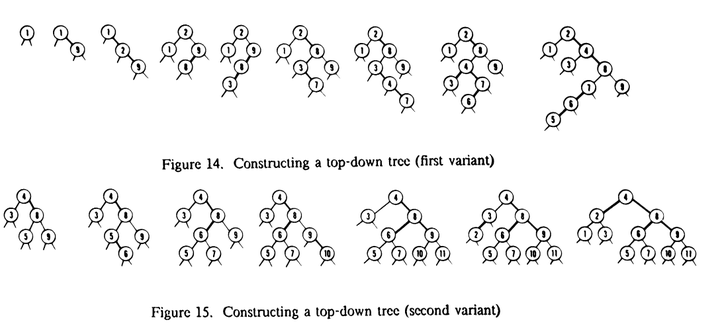
第三部分主要讨论了树的其他特性和相关算法。一种一次遍历的自顶向下删除算法,可以在一次遍历中完成删除操作。对算法的性能进行了比较分析。通过他们的实证观察和仿真研究,发现各种算法在平均情况下的性能差异很小。所以,作者建议在大多数应用中使用自顶向下算法,因为它们更简单。
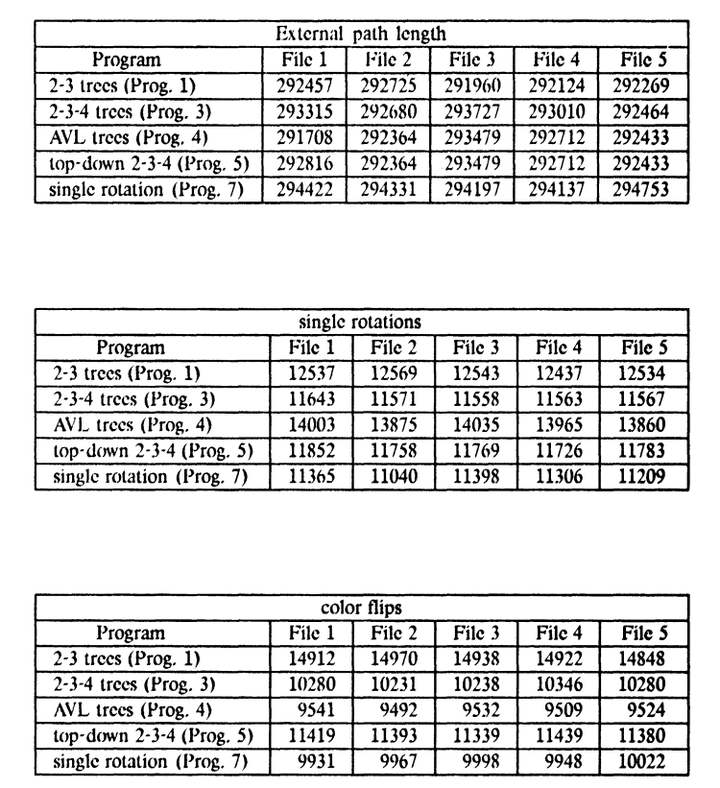
由此可知,推荐使用红黑树的原因是即使在相同的效率下,它的实现更简单、内存占用更少。AVL的平衡条件太苛刻,左右子树的高度差不能超过1,否则就要出发复杂的rebalance操作,苛刻条件会导致开销不能功过相抵,在写操作频繁的操作中,AVL似乎并不能很好的适应。
二、红黑树性质的简单推导
根据《A dichromatic framework for balanced trees》论文第一部分的说明,我们可以适当的进行推导。红黑树并不是AVL这种顺应逻辑的条件,可以从红黑树的近亲 2-3树进行演示。
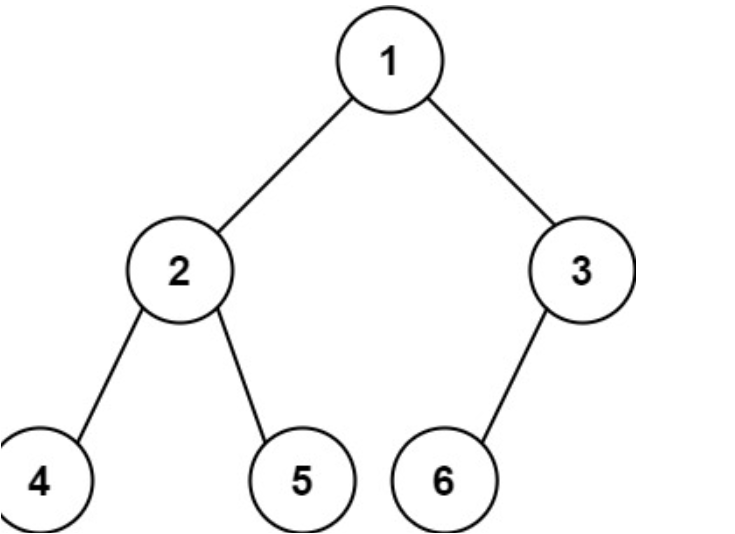
2-3树在插入过程中不断增长出新的根,使得树的高度不断增高,底层节点高度永远相等,忽略2节点和3节点的差异后会发现这是一颗完全二叉树,所有节点的高度都相等,是一颗完美的AVL树。
如果将其全部的3节点展开,展开时通过红色边链接展开后的子节点构造成一颗二叉树,比如:
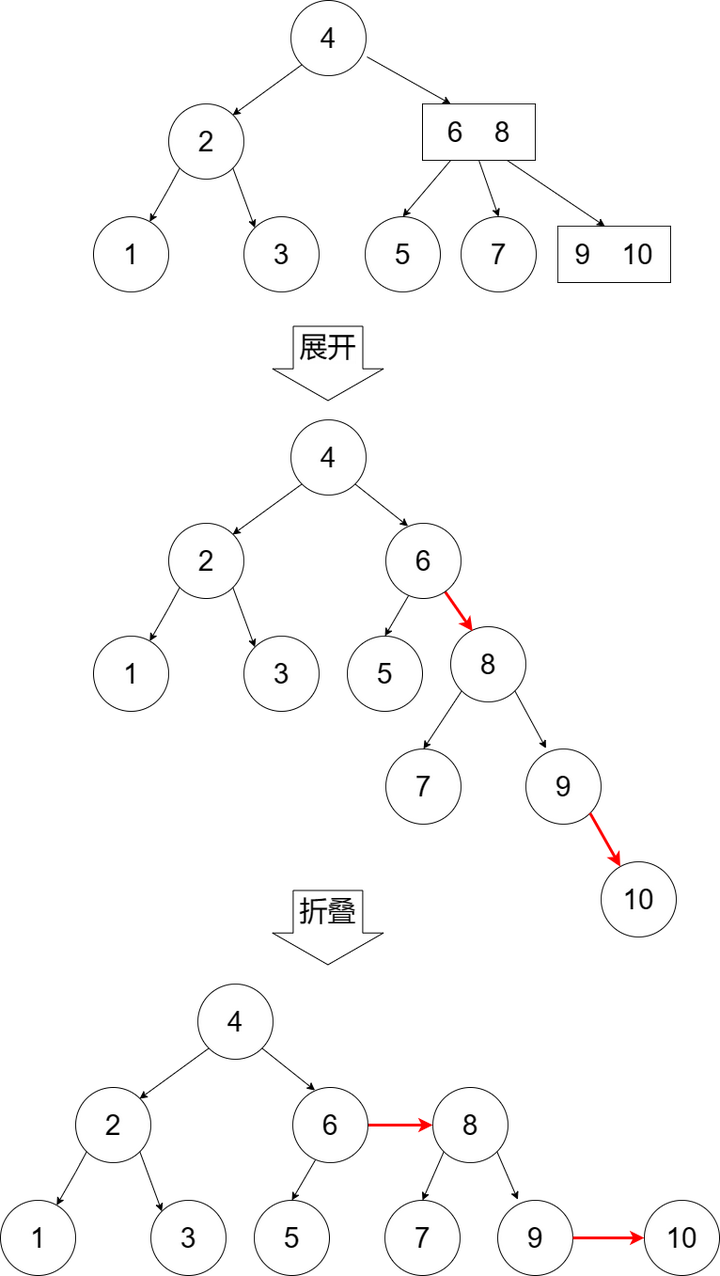
把当前节点同父节点之间的边的颜色计作节点的颜色,可得:
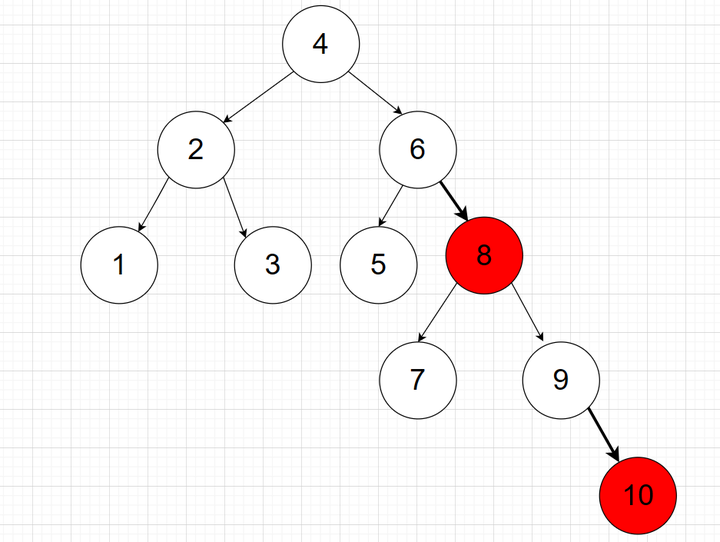
这就是这颗2-3树唯一对应的红黑树,从展开前的情况可以知道,未展开红色节点前,所有节点的高度完全一致,展开红色节点后,忽略掉红色节点,所有节点的黑高就是完全一致的,这就是红黑二叉树的性质之一:从任一节点到其每个叶子节点的简单路径上,所有黑色节点的数量相等。
由展开过程和分配节点颜色可知只有父节点原来是3节点时,才会将一个父节点中的一个染色为红色,但是展开后,该红色父节点变成了2节点,不会对该节点进行展开操作,所以该节点的子节点一定是黑色,这也是红黑树的性质之一:红色节点的子节点必须是黑色,不能有两个连续的红色节点。
三、结论
(1)红黑树不是由 AVL演变来的,而是推导出来的。由Rudolf Bayer在1972年引入,然后由Leonidas J. Guibas和Robert Sedgewick在1978年进行了改进。红黑树放宽了平衡的要求,它要求每个节点具有颜色属性(红色或黑色),并通过一些约束来确保树的大致平衡。虽然红黑树的平衡性不如AVL树严格,但由于其相对较少的旋转操作,红黑树在实际应用中表现出更好的性能。
(2)红黑树没有像AVL一样严格的深度差要求,但是要求从任一节点到其每个叶子节点的简单路径上,所有黑色节点的数量相等。
(3)红黑树最开始被引入来解决在动态数据结构中需要保持平衡的问题。它的设计目标是在维护二叉搜索树的基本性质的同时,尽量减少频繁的平衡操作,从而提高插入、删除和查找等操作的效率。
(4)红黑树的应用:
- 红黑树常被用作关联容器的底层实现,例如在C++的STL中,std::map 和 std::set 就是基于红黑树实现的。
- 红黑树在存储和数据库系统中也有应用。例如,在数据库索引中,红黑树可以用来维护数据的有序性,从而支持高效的数据检索操作。
- 在操作系统和调度算法中,红黑树也可以用于管理各种任务和事件,以保持任务的有序性和高效的操作。比如Linux的公平调度算法CFS。
- 在编译器优化中,红黑树可以用于构建符号表、优化搜索等。