一、前言
最近做多边形相关的工作,涉及比较多相关算法,总结一下,方便大家,如果帮到您,记得点赞!
二、演示
【在线演示】
【源码gitee】
三、使用
所有核心算法都在utils.js里面,含参数说明,如果不懂看可以看demo的使用。
3.1 多边形缩放
3.1.1 算法
参考:https://blog.csdn.net/sun_and_breeze/article/details/107517088
参考:https://blog.csdn.net/shyjhyp11/article/details/126396170
3.1.2 使用:
需配合‘顺时针判断’方法一起使用
const polygon = [
{ x: 314, y: 61 },
{ x: 385, y: 128 },
{ x: 496, y: 35 },
{ x: 390, y: 182 },
];
// 多边形放大5个单位
const zoomInPolygon = scalePolygon(polygon, 5); // 返回放大后多边形坐标集合
// 多边形缩小5个单位
const zoomOutPolygon = scalePolygon(polygon, -5); // 返回缩小后多边形坐标集合
3.1.3 演示:
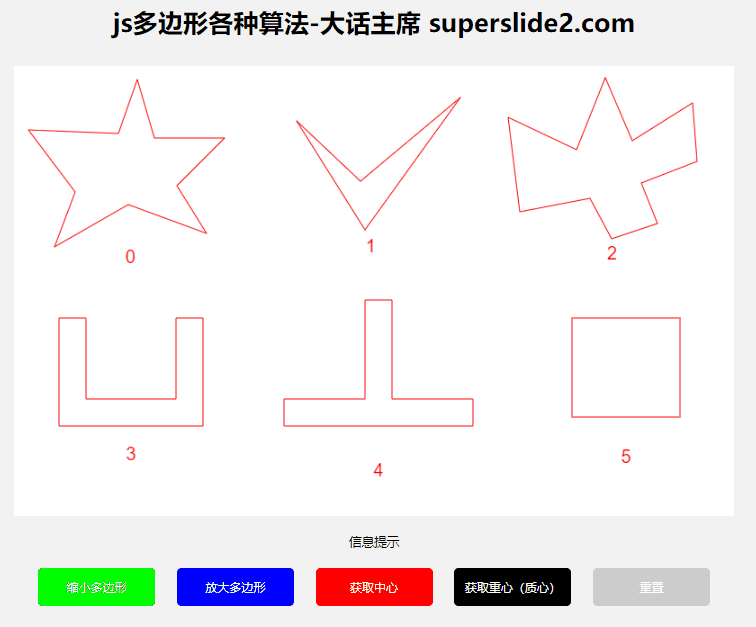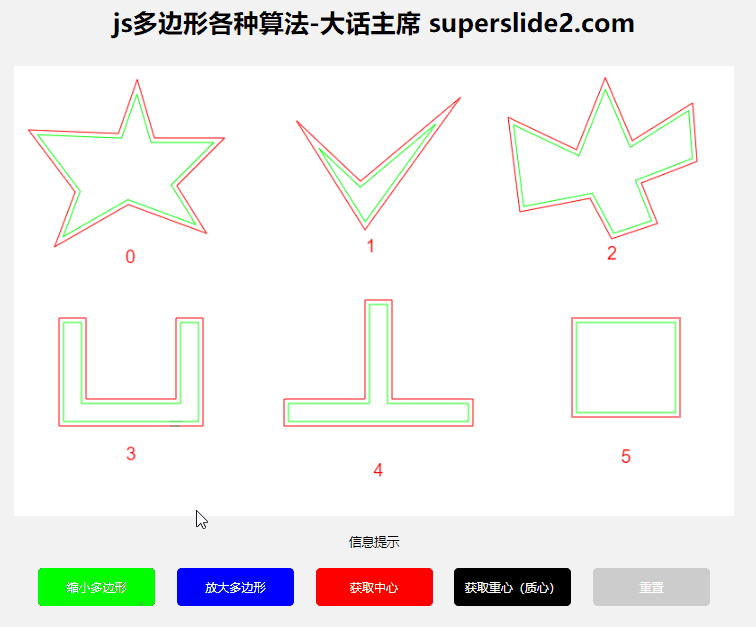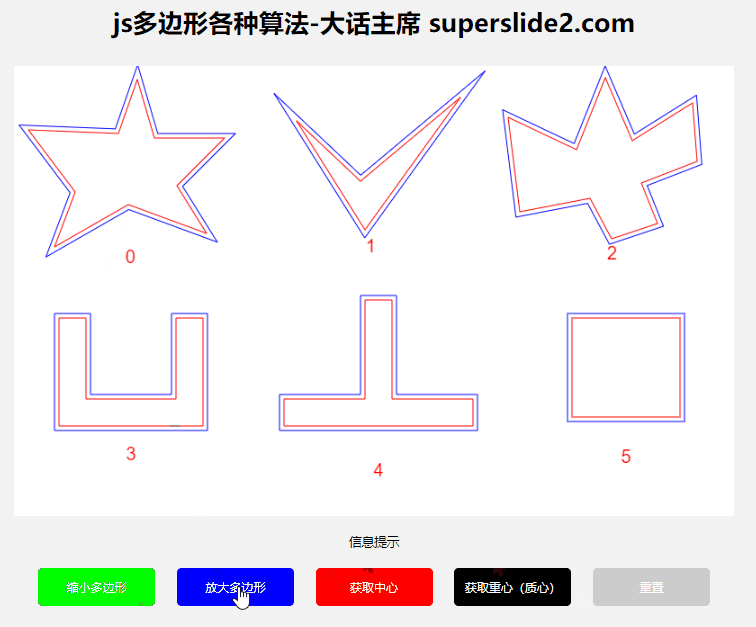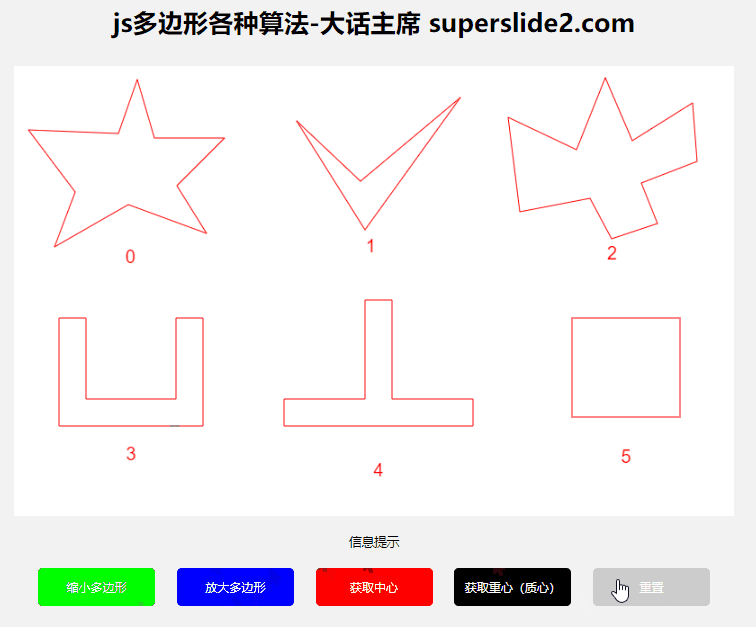
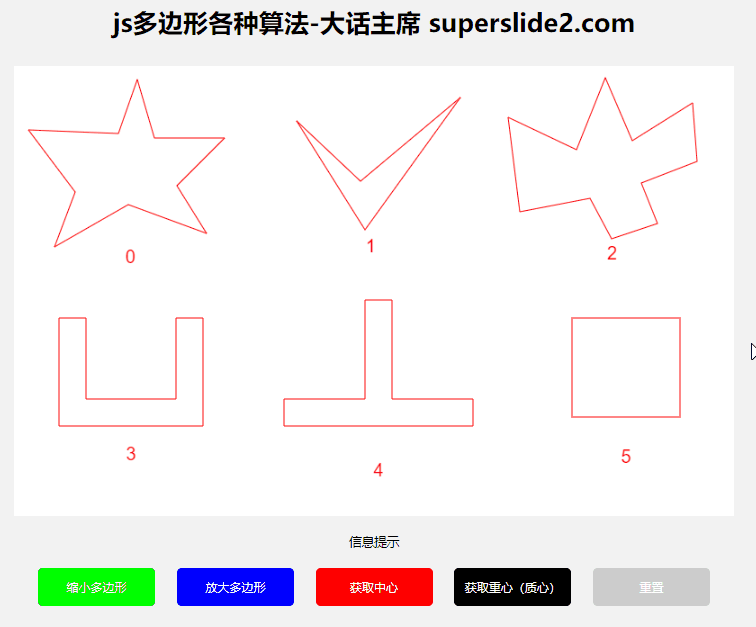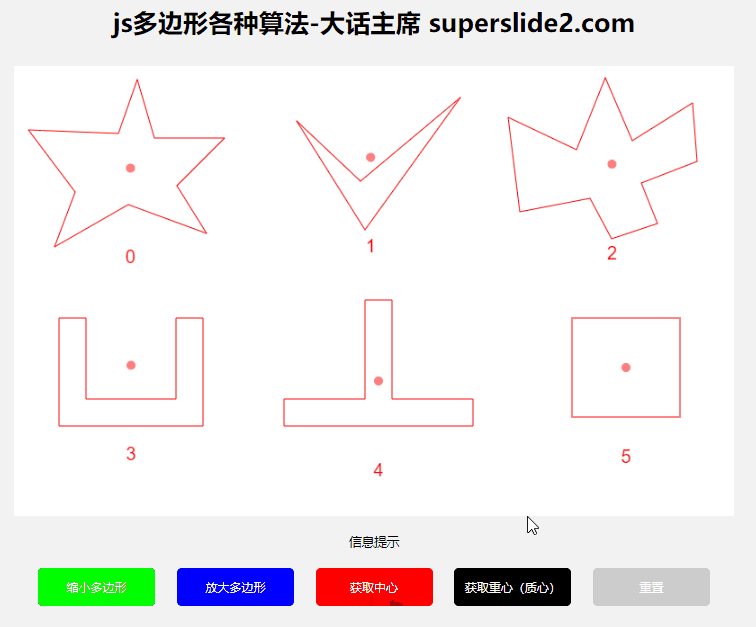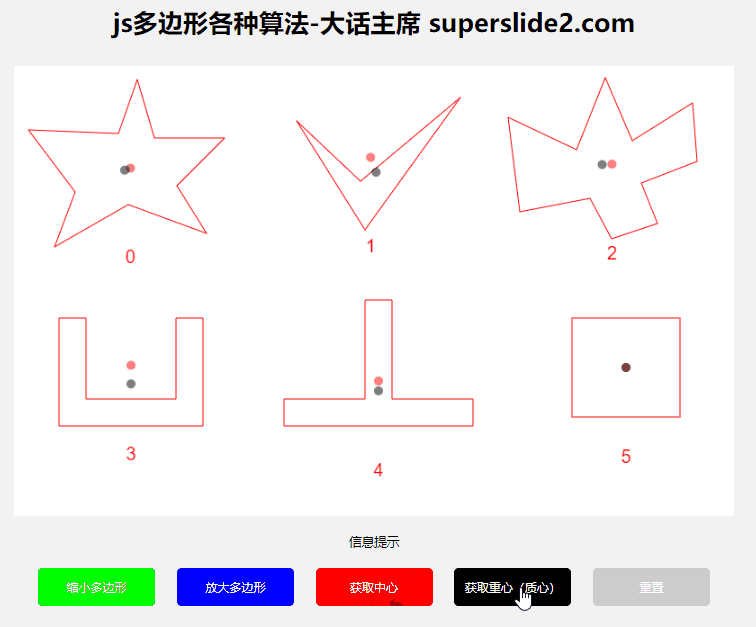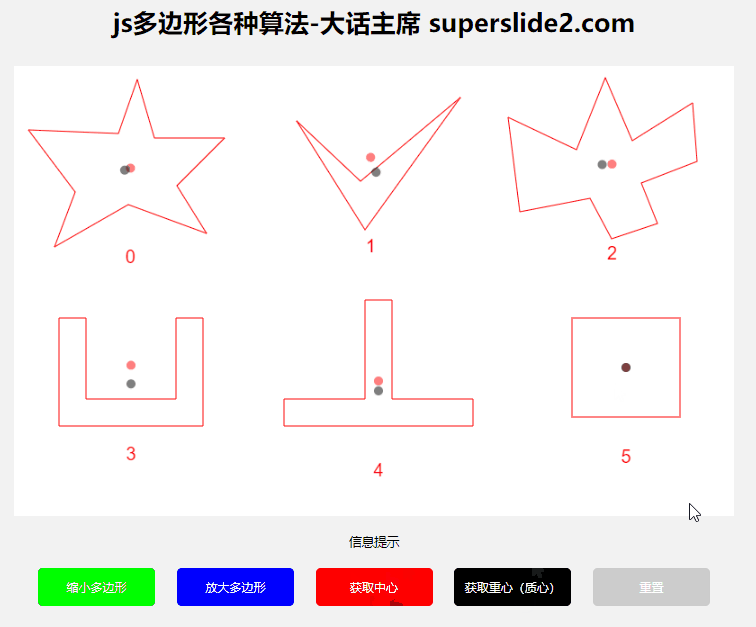
3.2 获取多边形中心、重心/质心
多边形中心和重心是不同的,如果是规则多边形则都一样,如果是凹多边形,很多情况下中心会在图形外面,所以需要根据实际情况取中心还是重心。
3.2.1 算法
中心算法:比较简单,就是所有坐标点加起来,求平均值
重心/质心算法参考:https://blog.csdn.net/weixin_43847416/article/details/95781817
3.2.2 使用
const polygon = [
{ x: 314, y: 61 },
{ x: 385, y: 128 },
{ x: 496, y: 35 },
{ x: 390, y: 182 },
];
// 获取多边形中心
const center = getPolygonCenter(polygon); // 返回坐标点
// 获取多边形重心/质心
const baryCenter = getPolygonBaryCenter(polygon); // 返回坐标点
3.2.3 演示
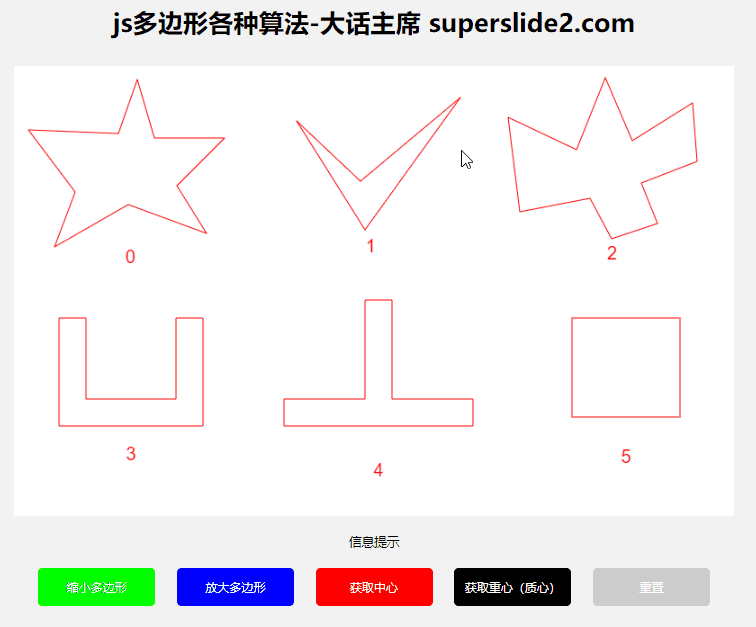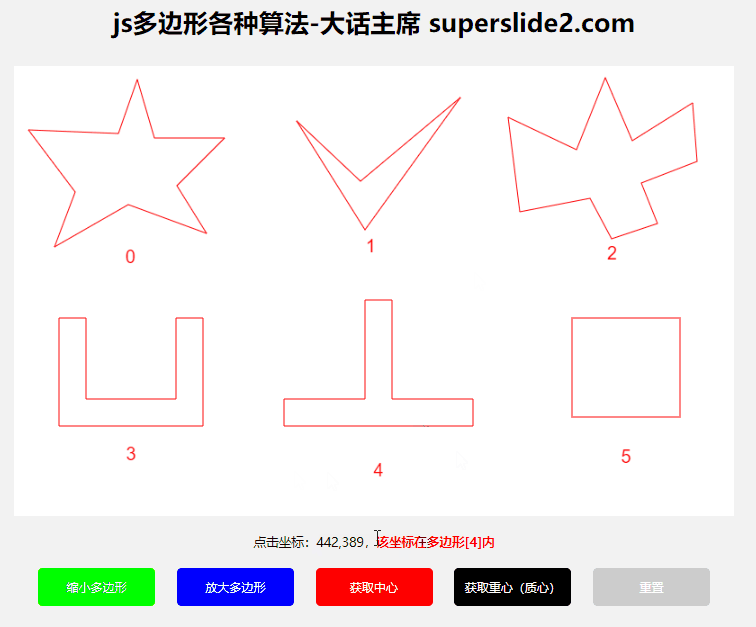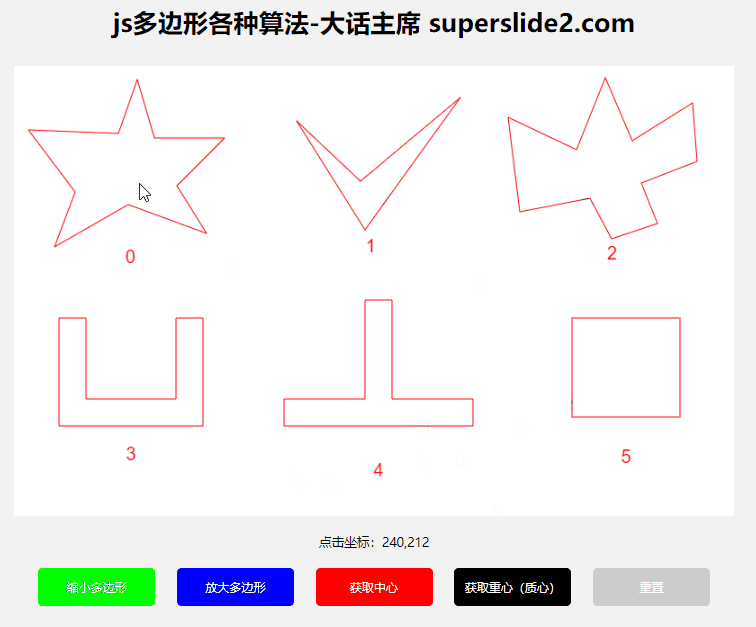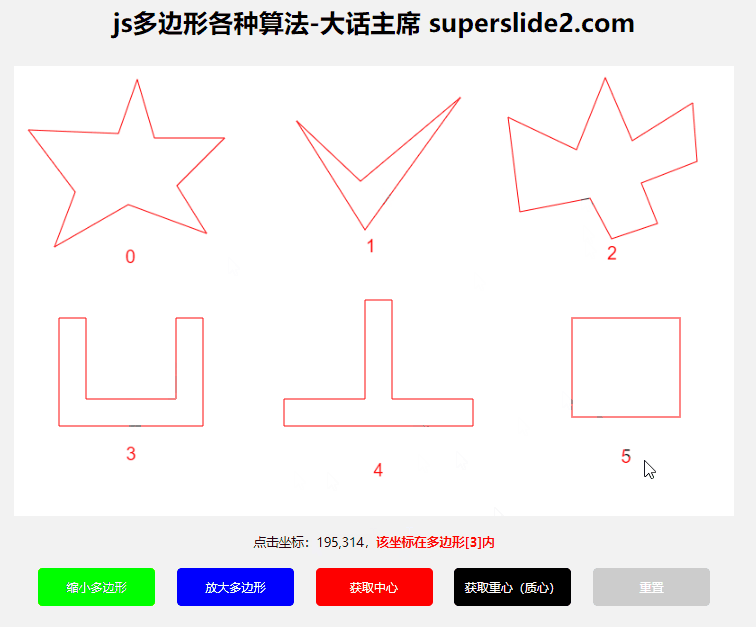
3.3 判断点是否在多边形内
3.3.1 算法
本例使用的是“射线法”
参考:https://blog.csdn.net/WilliamSun0122/article/details/77994526
3.3.2 使用
const point = { x: 322, y: 90 };
const polygon = [
{ x: 314, y: 61 },
{ x: 385, y: 128 },
{ x: 496, y: 35 },
{ x: 390, y: 182 },
];
// 判断点是否在多边形内部
const isIn = isInPolygon(point,polygon); // true or false
3.3.3 演示
3.4 判断多边形是否顺时针
3.4.1 算法
参考:https://blog.csdn.net/qq_34447899/article/details/93991335
3.4.1 使用
const polygon = [
{ x: 314, y: 61 },
{ x: 385, y: 128 },
{ x: 496, y: 35 },
{ x: 390, y: 182 },
];
// 判断多边形坐标是否顺时针
const isClock = isClockwise(polygon); // true or false
3.4.2 演示
这里就不演示了
四、核心代码
/*
* @Author: 大话主席 superslide2.com
* @Description: 多边形核心算法
*/
/**
* 获取多边形中心点
* @param {Point[]} points 点坐标数组 [{x:0,y:0}...]
*/
function getPolygonCenter(points) {
if (!Array.isArray(points) || points.length < 3) {
console.error("多边形坐标集合不能少于3个");
return;
}
const result = { x: 0, y: 0 };
points.forEach((p) => {
result.x += p.x;
result.y += p.y;
});
result.x /= points.length;
result.y /= points.length;
return result;
}
/**
* 获取多边形重心(质心)
* @param {Point[]} points 点坐标数组 [{x:0,y:0}...]
*/
function getPolygonBaryCenter(points) {
if (!Array.isArray(points) || points.length < 3) {
console.error("多边形坐标集合不能少于3个");
return;
}
const result = { x: 0, y: 0 };
let area = 0;
for (let i = 1; i <= points.length; i++) {
const curX = points[i % points.length].x;
const curY = points[i % points.length].y;
const nextX = points[i - 1].x;
const nextY = points[i - 1].y;
const temp = (curX * nextY - curY * nextX) / 2;
area += temp;
result.x += (temp * (curX + nextX)) / 3;
result.y += (temp * (curY + nextY)) / 3;
}
result.x /= area;
result.y /= area;
return result;
}
/**
* 判断点是否在多边形内部
* @param {Point} point 点坐标
* @param {Point[]} points 点坐标数组 [{x:0,y:0}...]
* @returns
*/
function isInPolygon(point, points) {
if (!Array.isArray(points) || points.length < 3) {
console.error("多边形坐标集合不能少于3个");
return;
}
const n = points.length;
let nCross = 0;
for (let i = 0; i < n; i++) {
const p1 = points[i];
const p2 = points[(i + 1) % n];
// 求解 y=p.y 与 p1 p2 的交点
// p1p2 与 y=p0.y平行
if (p1.y === p2.y) continue;
// 交点在p1p2延长线上
if (point.y < Math.min(p1.y, p2.y)) continue;
// 交点在p1p2延长线上
if (point.y >= Math.max(p1.y, p2.y)) continue;
// 求交点的 X 坐标
const x = ((point.y - p1.y) * (p2.x - p1.x)) / (p2.y - p1.y) + p1.x;
// 只统计单边交点
if (x > point.x) nCross++;
}
return nCross % 2 === 1;
}
/**
* 缩放多边形坐标
* @decoration 需配合顺时针判断方法一起使用
* @param {Point[]} points 点坐标数组 [{x:0,y:0}...]
* @param {number} extra 外延大小。为正: 向外扩; 为负: 向内缩
* @return {Point[]} 扩展或缩小后的多边形点坐标数组
*/
function scalePolygon(points, extra) {
if (!Array.isArray(points) || points.length < 3) {
console.error("多边形坐标集合不能少于3个");
return;
}
const ps = points;
// 通过顺时针判断取正值还是负值
const extra0 = isClockwise(ps) ? -extra : extra;
const norm = (x, y) => Math.sqrt(x * x + y * y);
const len = ps.length;
const polygon = [];
for (let i = 0; i < len; i++) {
const point = ps[i];
const point1 = ps[i === 0 ? len - 1 : i - 1];
const point2 = ps[i === len - 1 ? 0 : i + 1];
// 向量PP1
const vectorX1 = point1.x - point.x; // 向量PP1 横坐标
const vectorY1 = point1.y - point.y; // 向量PP1 纵坐标
const n1 = norm(vectorX1, vectorY1); // 向量的平方根 为了对向量PP1做单位化
let vectorUnitX1 = vectorX1 / n1; // 向量单位化 横坐标
let vectorUnitY1 = vectorY1 / n1; // 向量单位化 纵坐标
// 向量PP2
const vectorX2 = point2.x - point.x; // 向量PP2 横坐标
const vectorY2 = point2.y - point.y; // 向量PP2 纵坐标
const n2 = norm(vectorX2, vectorY2); // 向量的平方根 为了对向量PP1做单位化
let vectorUnitX2 = vectorX2 / n2; // 向量单位化 横坐标
let vectorUnitY2 = vectorY2 / n2; // 向量单位化 纵坐标
// PQ距离
const vectorLen =
-extra0 /
Math.sqrt(
(1 - (vectorUnitX1 * vectorUnitX2 + vectorUnitY1 * vectorUnitY2)) / 2
);
// 根据向量的叉乘积来判断角是凹角还是凸角
if (vectorX1 * vectorY2 + -1 * vectorY1 * vectorX2 < 0) {
vectorUnitX2 *= -1;
vectorUnitY2 *= -1;
vectorUnitX1 *= -1;
vectorUnitY1 *= -1;
}
// PQ的方向
const vectorX = vectorUnitX1 + vectorUnitX2;
const vectorY = vectorUnitY1 + vectorUnitY2;
const n = vectorLen / norm(vectorX, vectorY);
const vectorUnitX = vectorX * n;
const vectorUnitY = vectorY * n;
const polygonX = vectorUnitX + point.x;
const polygonY = vectorUnitY + point.y;
polygon[i] = { x: polygonX, y: polygonY };
}
return polygon;
}
/**
* 判断坐标数组是否顺时针(默认为false)
* @param {Point[]} points 点坐标数组 [{x:0,y:0}...]
* @returns {boolean} 是否顺时针
*/
function isClockwise(points) {
// 三个点可以判断矢量是顺时针旋转还是逆时针旋转的,但由于可能存在凹边,所以并不是任意三点都可以正确反映多边形的走向
// 因此需要取多边形中绝对是凸边的点来判断,
// 多边形中的极值点(x最大或x最小或y最大或y最小)它与相邻两点构成的边必然是凸边,因此我们先取出多边形中的极值点,再由极值点和其前后两点去判断矢量的走向,从而判断出多边形的走向。
if (!Array.isArray(points) || points.length < 3) {
console.error("多边形坐标集合不能少于3个");
return false;
}
let coords = JSON.parse(JSON.stringify(points));
if (coords[0] === coords[coords.length - 1]) {
coords = coords.slice(0, coords.length - 1);
}
coords = coords.reverse();
let maxXIndex = 0;
let maxX = parseFloat(coords[maxXIndex].x);
let c1;
let c2;
let c3;
for (let i = 0; i < coords.length; i++) {
if (parseFloat(coords[i].x) > maxX) {
maxX = parseFloat(coords[i].x);
maxXIndex = i;
}
}
if (maxXIndex === 0) {
c1 = coords[coords.length - 1];
c2 = coords[maxXIndex];
c3 = coords[maxXIndex + 1];
} else if (maxXIndex === coords.length - 1) {
c1 = coords[maxXIndex - 1];
c2 = coords[maxXIndex];
c3 = coords[0];
} else {
c1 = coords[maxXIndex - 1];
c2 = coords[maxXIndex];
c3 = coords[maxXIndex + 1];
}
const x1 = parseFloat(c1.x);
const y1 = parseFloat(c1.y);
const x2 = parseFloat(c2.x);
const y2 = parseFloat(c2.y);
const x3 = parseFloat(c3.x);
const y3 = parseFloat(c3.y);
const s = (x1 - x3) * (y2 - y3) - (x2 - x3) * (y1 - y3);
return s < 0;
}
五、点赞
如果帮到您,点个赞再走!




![[附源码]Python计算机毕业设计飞羽羽毛球馆管理系统Django(程序+LW)](https://img-blog.csdnimg.cn/a3b15daef2cb4ab881d9ee97f7ebbb57.png)