目录
62. 不同路径
63. 不同路径 II
62. 不同路径
类型:动态规划
难度:medium

思路:
应用二维数组的动态规划,到达某个方格的方法数目,为这个方格的上一个方格和左一个方格的方法数目和。
需要先初始化第一行和第一列为1。
代码:
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
// 初始化第一列
for (int i = 0; i < m; i++) {
dp[i][0] = 1;
}
// 初始化第一行
for (int i = 0; i < n; i++) {
dp[0][i] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
}63. 不同路径 II
类型:动态规划
难度:medium

思路:
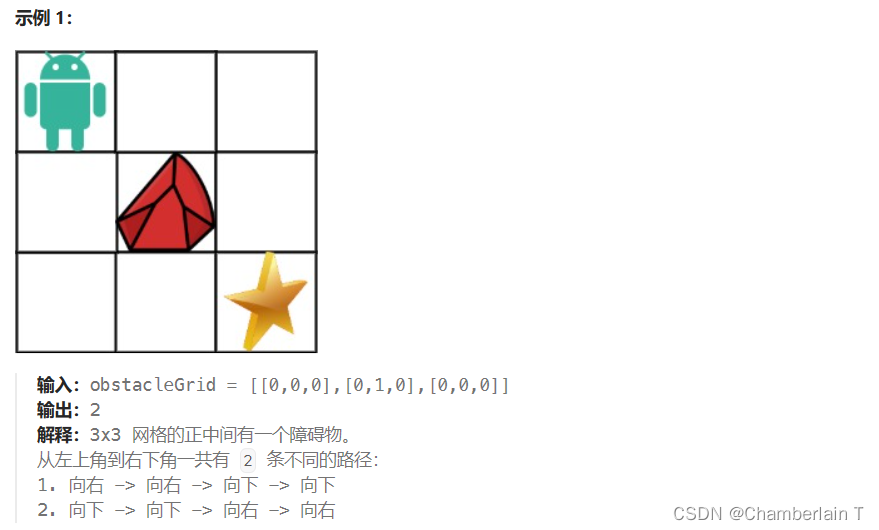
与上一题不同的是,当障碍物出现时:
对于第一行和第一列:某个方格出现障碍物之后,该方格后的方格则无法到达,初始化为0。
对于第一行和第一列之外:某个方格出现障碍物,该方格的dp设置为0。
代码:
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int h = obstacleGrid.length;
int w = obstacleGrid[0].length;
// int数组默认0
int[][] dp = new int[h][w];
// 初始化第一列
for (int i = 0; i < h; i++) {
if (obstacleGrid[i][0] == 1) {
break;
}
dp[i][0] = 1;
}
// 初始化第一行
for (int i = 0; i < w; i++) {
if (obstacleGrid[0][i] == 1) {
break;
}
dp[0][i] = 1;
}
for (int i = 1; i < h; i++) {
for (int j = 1; j < w; j++) {
if (obstacleGrid[i][j] == 1) {
dp[i][j] = 0;
} else {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
}
return dp[h - 1][w - 1];
}
}