刷题顺序及思路来源于代码随想录,网站地址:https://programmercarl.com
目录
404. 左叶子之和
513. 找树左下角的值
递归
迭代
112. 路径总和
113. 路径总和 II
404. 左叶子之和
给定二叉树的根节点 root ,返回所有左叶子之和。

/**
* @author light
* @Description 左叶子之和
* 给定二叉树的根节点 root ,返回所有左叶子之和。
*
* (判断该节点是否是左叶子不能靠当前结点判断,而是靠父节点其左孩子是不是来判断的
* @create 2023-08-19 10:17
*/
public class SumOfLeftLeavesTest {
public static int sumOfLeftLeaves(TreeNode root) {
//终止条件
if(root==null){
return 0;
}
//只有当前遍历的结点是父节点时,才能判断其子节点是否是左叶子
if(root.left==null&&root.right==null){
return 0;
}
//后序遍历
int leftNum=sumOfLeftLeaves(root.left); //左
if(root.left!=null&&root.left.left==null&&root.left.right==null){
leftNum=root.left.val;
}
int rightNum=sumOfLeftLeaves(root.right); //右
int sum=leftNum+rightNum;//中
return sum;
}
}
513. 找树左下角的值
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。

递归
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int maxDepth=Integer.MIN_VALUE; //记录最大深度
public int value;
public int findBottomLeftValue(TreeNode root) {
findValue(root,0);
return value;
}
private void findValue(TreeNode root, int depth) {
if(root.left==null&&root.right==null){
if(maxDepth<depth){
maxDepth=depth;
value= root.val;
}
}
if(root.left!=null){
depth++;
findValue(root.left,depth);
depth--;
}
if(root.right!=null){
depth++;
findValue(root.right,depth);
depth--;
}
}
}迭代
层序遍历,记录最后一层第一的节点即可
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int findBottomLeftValue(TreeNode root) {
int value=0;
if(root==null){
return value;
}
Deque<TreeNode> que=new ArrayDeque<>();
que.offer(root);
while(!que.isEmpty()){
int size=que.size();
int count=size;
while(size>0){
TreeNode node=que.poll();
if(count==size){
value= node.val;
}
if(node.left!=null){
que.offer(node.left);
}
if(node.right!=null){
que.offer(node.right);
}
size--;
}
}
return value;
}
}112. 路径总和
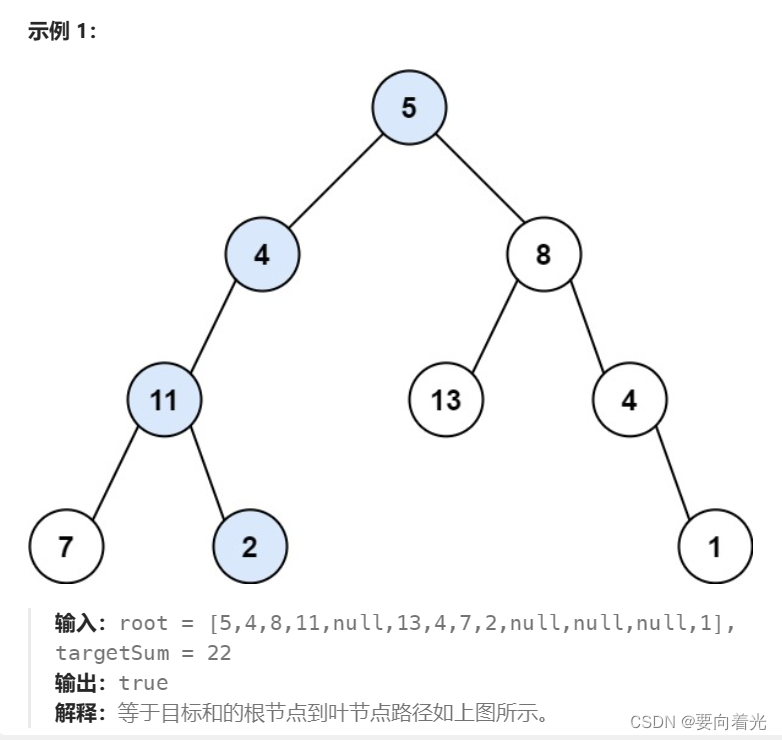
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
/**
* @author light
* @Description 路径总和
*
* (不要去累加然后判断是否等于目标和,那么代码比较麻烦,可以用递减,
* 让计数器count初始为目标和,然后每次减去遍历路径节点上的数值。
*
* 如果最后count == 0,同时到了叶子节点的话,说明找到了目标和。
*
* 如果遍历到了叶子节点,count不为0,就是没找到。
* @create 2023-08-19 11:48
*/
public class HasPathSumTest {
public boolean hasPathSum(TreeNode root, int targetSum) {
if(root==null){
return false;
}
targetSum-=root.val;
if(root.left==null&&root.right==null){
return targetSum==0;
}
if(root.left!=null){
targetSum-=root.left.val;
boolean left=hasPathSum(root.left,targetSum);
if(left){
return true; //找到了
}
targetSum+=root.left.val;
}
if(root.right!=null){
targetSum-=root.right.val;
boolean right=hasPathSum(root.right,targetSum);
if(right){
return true; //找到了
}
targetSum+=root.right.val;
}
return false;
}
}
113. 路径总和 II
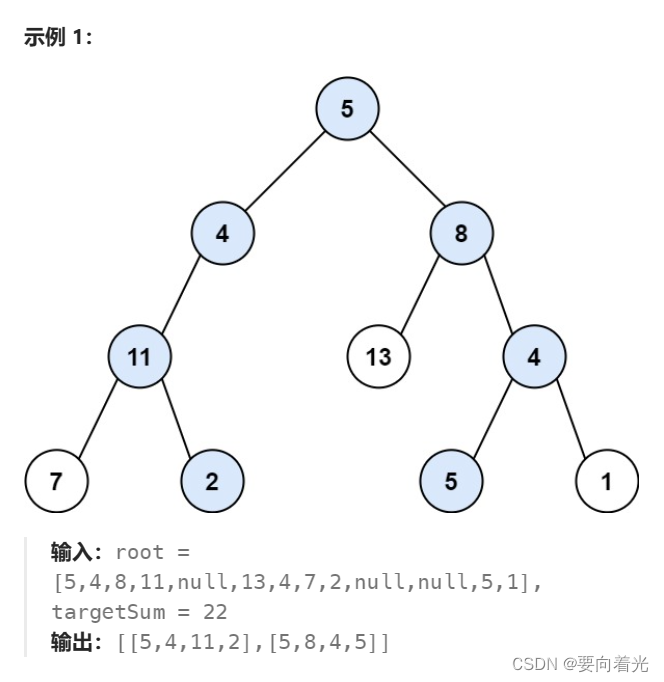
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> res=new ArrayList<>(); //存放结果集
List<Integer> path=new ArrayList<>(); //存放路径变量
if(root==null){
return res;
}
getPaths(root,targetSum,path,res);
return res;
}
private void getPaths(TreeNode root, int targetSum, List<Integer> path, List<List<Integer>> res) {
path.add(root.val);
if(root.left==null&&root.right==null){
if(targetSum-root.val==0){
res.add(new ArrayList<>(path));
}
return;
}
if(root.left!=null){
targetSum-=root.val;
getPaths(root.left,targetSum,path,res);
path.remove(path.size()-1);
targetSum+=root.val;
}
if(root.right!=null){
targetSum-=root.val;
getPaths(root.right,targetSum,path,res);
path.remove(path.size()-1);
targetSum+=root.val;
}
}
}