目录
STL六大组件介绍
容器
序列式容器
vector
list
知识点考察
关联式容器
map/set
set介绍
set常用接口
map介绍
map常用接口
底层结构：红黑树
unordered_map/set
unordered_map/set介绍
底层结构：哈希表
知识考察
适配器
stack
queue
priority_queue
迭代器
什么是迭代器
迭代器的定义
迭代器失效
迭代器分类
STL六大组件介绍
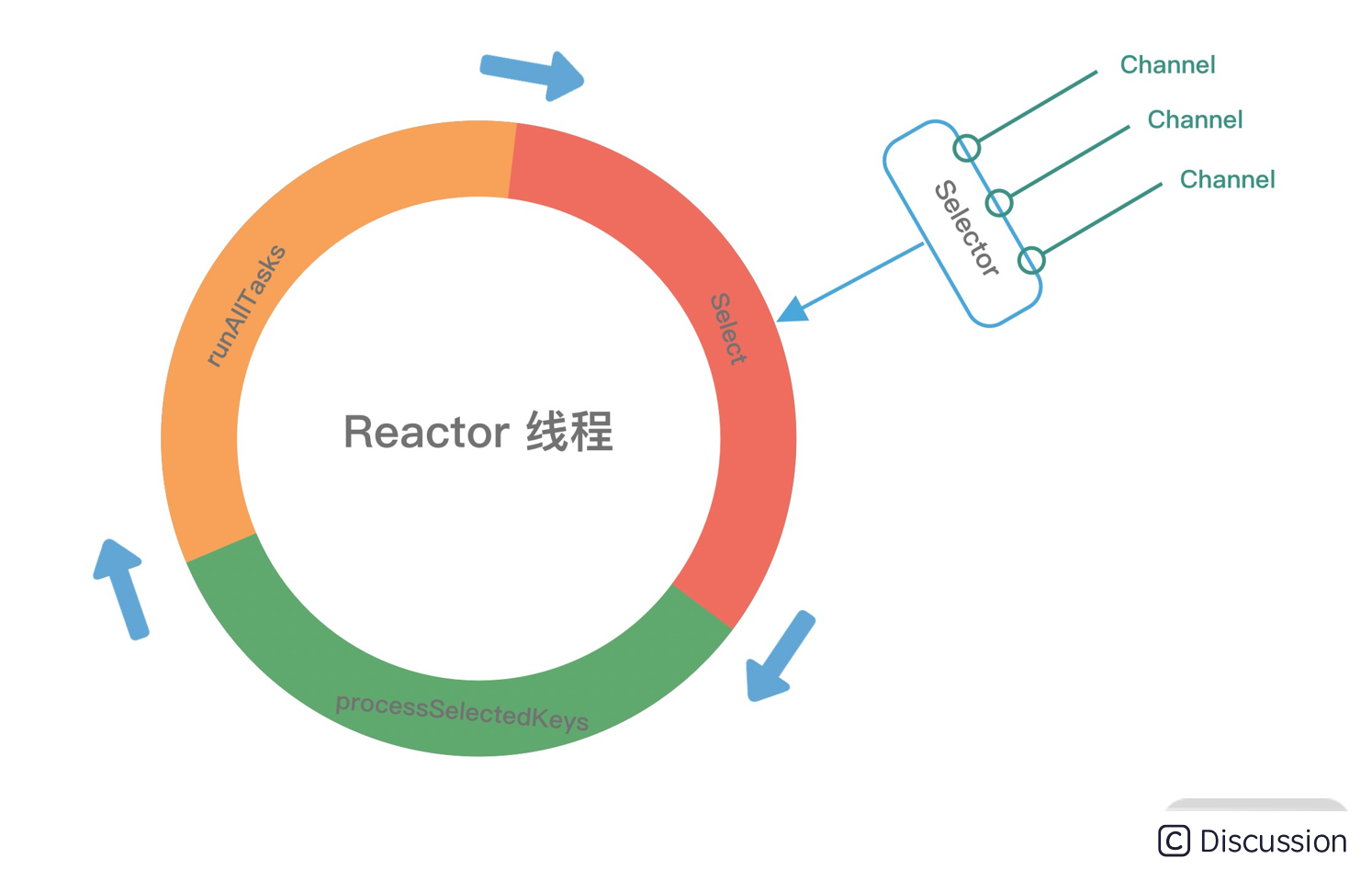
从使用的角度来看，重点关注容器、算法和迭代器三个组件：
在使用C++进行程序编写的过程中，容器的使用必不可少，如用vector/list/map等来进行数据的存储。算法可以非常便捷的对容器进行操作，比如用sort对vector中的数据排序，使用find在map中查找元素等等。在通过算法操作容器的时候，不得不提到迭代器，它就像是容器和算法间的粘合剂：
迭代器的存在，首先封装隐藏了底层的实现细节。其次，为用户提供了统一的方式去访问容器，极大的降低了使用的成本。
从底层的角度，分析各个组件的功能及联系：
容器：各种数据结构，如: vector，list，set，map用来存放数据。
算法：各种常用算法如sort，swap，reverse，find等。
迭代器：扮演容器与算法之间的胶合剂。从实现角度来看，迭代器将operator*， operator->, operator++, operator--等相关操作进行重载的类。所有STL容器都附带有自己专属的迭代器，用户可以用统一的方式对容器进行访问。
仿函数：实现了operator()，这个类能够像函数一样调用，函数指针可视为狭义的仿函数。可作为算法的某种策略，例如改变sort排序的比较规则，map/set的key比较大小的规则。
配接器：用来修饰容器、仿函数、迭代器接口。如：stack，queue，主要体现了复用。
配置器：负责空间配置与管理，从实现角度来看，配置器实现了动态空间配置，空间管理，空间释放。例如：容器需要频繁的申请和释放小块的内存，这种情况下可以使用空间配置器，提高效率。
容器
序列式容器
vector
介绍：vector是表示可变大小数组的序列式容器，采用连续存储空间来存储元素，支持下标的随机访问，它的大小是可以动态改变的。vector在访问元素、尾插和尾删的场景下相对高效。
如上图所示，vector底层设计通过三个迭代器的指针分别记录数据块的起始位置，末尾有效数据和存储容量的末尾位置。vector的迭代器是原生的指针。
vector常用接口：
push_back:尾插
pop_back：尾删
operator[]：[]重载，使vector可以向数组一样访问。
rsize:改变vector的size，在开辟空间的同时还会初始化。
resrve：改变vector的capacity。
list
list的底层结构是双向链表，该容器可以前后双向迭代。list在任意位置插入和删除元素的执行效率更好。
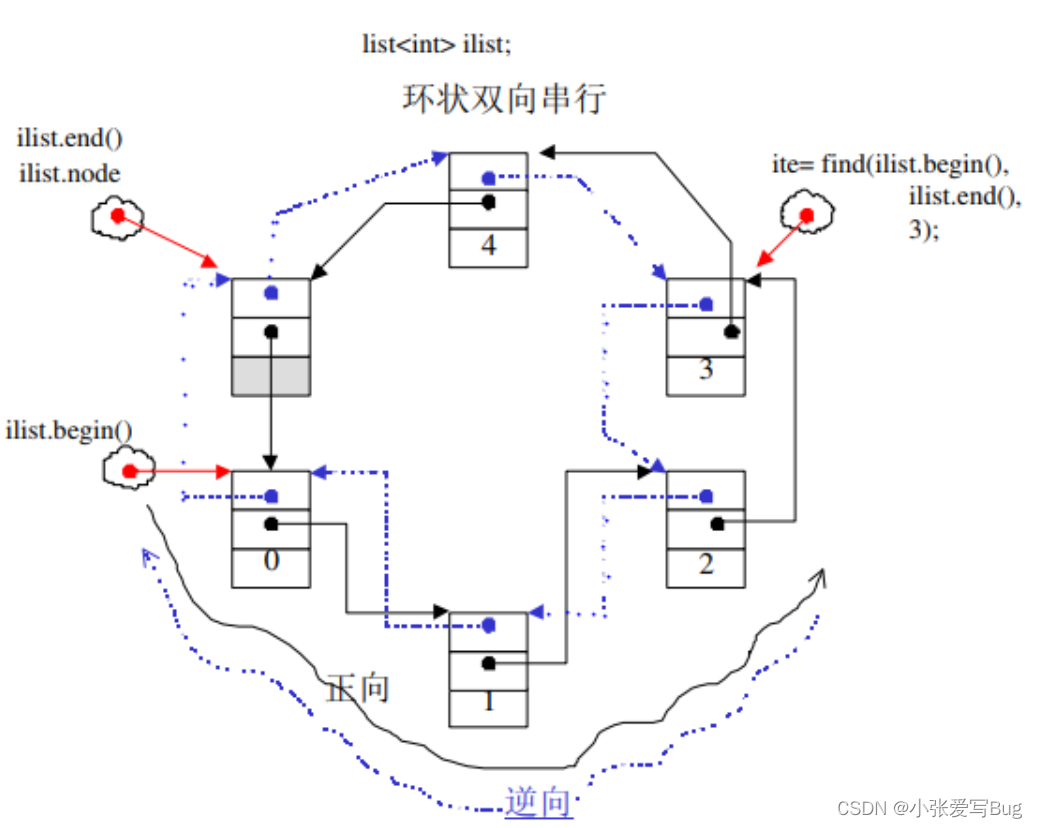
如上图所示，list_node的结构分为三个部分，分别是指向下一个节点的指针Next，执行前一个节点的指针Prev和存储数据的Val。
常用接口：
push_front/pop_front:头插、头删。
push_back/pop_back：尾插、尾删。
insert/erase:在pos位置插入值为val的元素,删除pos位置的元素。
知识点考察
vector和list的区别？
1.底层结构：vector采用连续的空间对数据进行存储（动态顺序表）。list物理结构不连续（带头节点的双向循环链表）。
2.随机访问：vector支持随机访问，访问某个元素的效率是O(1)。list不支持随机访问，访问某个元素的效率是O(n)。
3.迭代器：vector迭代器是原生的指针，list对原生态指针进行了封装。
4.使用场景：vector适合需要高效存储，支持随机访问，不关心插入删除效率的场景（中间插入要挪动数据，效率太低）。而list更适合大量的插入和删除操作，不关心随机访问的场景。
vector如何扩容？
当指向最后一个有效数据位置的迭代器和容量末尾的迭代器重合的时候，代表容器已满，需要进行扩容，在vs下按照1.5倍扩容，g++下按照2倍扩容。但这仅供参考，具体增长多少是根据具体的需求定义的，vs下是PJ版STL,g++是SGI版STL。主要原因就是，扩大了空间浪费，扩小了不够用频繁扩容，所以没有固定的标准说一定扩多少。
resize和reserve有什么区别？
resize在开辟空间的同时还会初始化，改变size的大小。reserve只负责开辟空间。
关联式容器
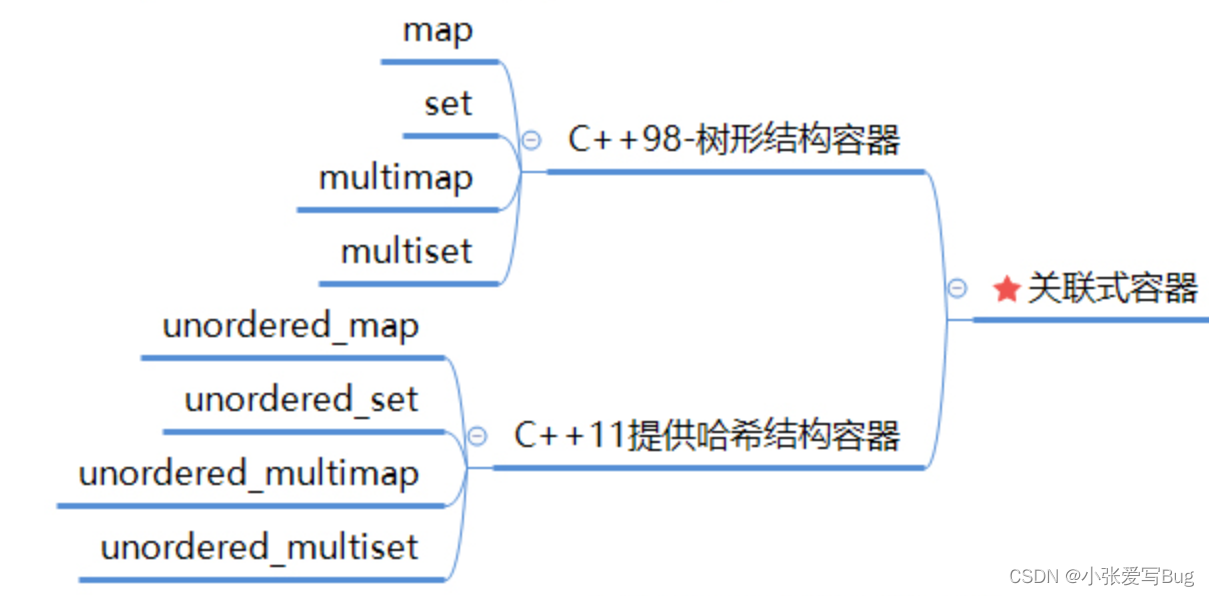
map/set
set介绍
1. 与map/multimap不同，map/multimap中存储的是真正的键值对<key, value>，set中只放
value，但在底层实际存放的是由<value, value>构成的键值对。 2. set中插入元素时，只需要插入value即可，不需要构造键值对。
3. set中的元素不可以重复(因此可以使用set进行去重)。
4. 使用set的迭代器遍历set中的元素，可以得到有序序列。
5. set中的元素默认按照小于来比较。
6. set中查找某个元素，时间复杂度为：$log_2 n$。
7. set中的元素不允许修改，修改方式是先删除在插入新的元素，直接修改会破坏set的有序性。
8. set中的底层使用二叉搜索树(红黑树)来实现。
set常用接口
empty：检测set是否为空。
size:：返回set中有效元素的个数。
insert：向set中插入元素x。
erase：删除set中pos位置上的元素。
find：返回set中值为x的元素的个数。
map介绍
1. map中的的元素是键值对
2. map中的key是唯一的，并且不能修改
3. 默认按照小于的方式对key进行比较。
4. map中的元素如果用迭代器去遍历，可以得到一个有序的序列
5. map的底层为平衡搜索树(红黑树)，查找效率比较高$O(log_2 N)$
6. 支持[]操作符，operator[]中实际进行插入查找，返回值是key对应的value。
map常用接口
operator[]:map支持下标访问符，即在[]中放入key，就可以找到与key对应的value。
empty：检测set是否为空。
size:：返回set中有效元素的个数。
insert：向set中插入元素x。
erase：删除set中pos位置上的元素。
find：返回set中值为x的元素的个数。
底层结构：红黑树
在介绍红黑树之前先介绍一下AVl树：
由于在极端的情况下，二叉搜索树可能会退化成单边树，此时查找效率就会退化成O(N)。AVL树的出现解决了上述问题，当新节点插入到AVL树中后，控制每个节点左右子树的高度差的绝对值不超过1。AVL树是高度平衡的二叉搜索树，搜索数据的时间复杂度为O(log_2 n)。
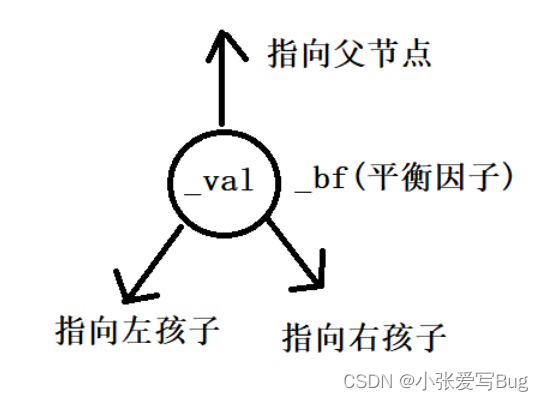
template<class K,class V>
class AVLTreeNode
{
public:
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
pair<K, V> _data;
int _bf;
AVLTreeNode(const pair<K,V>& kv)
:_left(nullptr), _right(nullptr)
, _parent(nullptr), _bf(0),_data(kv)
{}
};
AVL树的插入可以简单的分为两步，首先是按照二叉搜索的方式插入新节点，其次就是通过平衡因子调整树的平衡。下面重点关注什么情况下需要调整，如何进行调整。
节点pCur（新插入的节点）插入后，pParent（新节点的父节点）的平衡因子一定需要调整，在插入之前，pParent的平衡因子分为三种情况：-1，0, 1, 分以下两种情况：
1. 如果pCur插入到pParent的左侧，只需给pParent的平衡因子-1。
2. 如果pCur插入到pParent的右侧，只需给pParent的平衡因子+1。
此时：pParent的平衡因子可能有三种情况：0，正负1， 正负2
1. 如果pParent的平衡因子为0，说明插入之前pParent的平衡因子为正负1，插入后被调整
成0，此时满足AVL树的性质，插入成功
2. 如果pParent的平衡因子为正负1，说明插入前pParent的平衡因子一定为0，插入后被更
新成正负1，此时以pParent为根的树的高度增加，需要继续向上更新调整。
3. 如果pParent的平衡因子为正负2，则pParent的平衡因子违反平衡树的性质，需要对其进
行旋转处理。
AVl树的旋转可以大致的分为如下几种情况：
以左单旋为例：
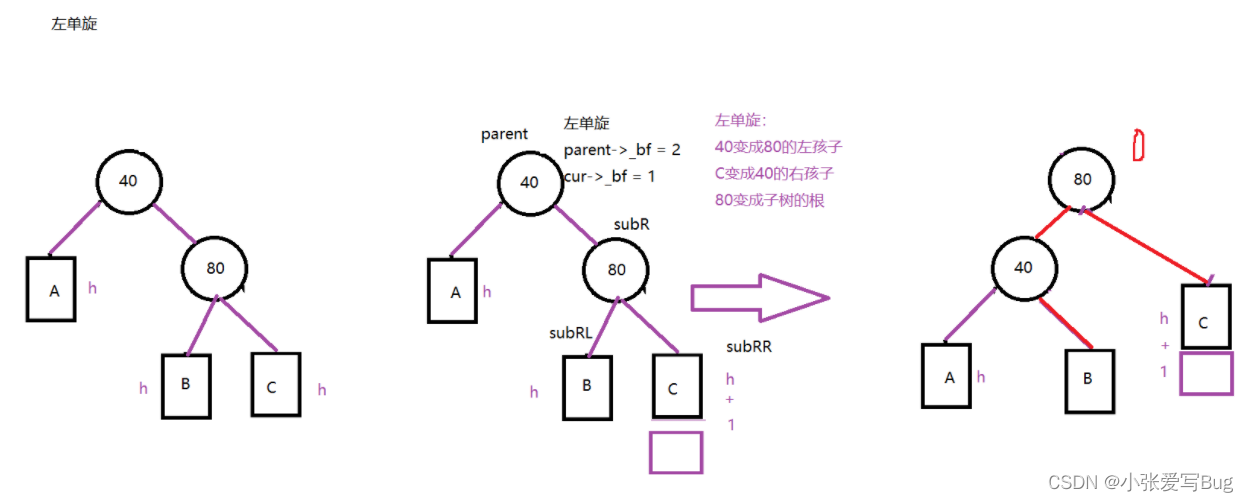
新节点插入较高左子树的右侧，左边低右边高，以40为根的二叉树不平衡。大致过程如下：
1.subRL变成parent的右孩子。
2.subR变成根节点。
3.parent变成subR的左孩子。
代码实现的过程中要注意几个点：旋转完后subR是该子树的根节点，它可能是整颗树的根节点也可能只是一颗子树。还要注意subRL是否为空。
void RotateL(Node* parent)
{
Node* SubR = parent->_right;
Node* SubRL = SubR->_left;
//cur的左孩子给parent的右
parent->_right = SubRL;
if (SubRL) SubRL->_parent = parent;
//cur变成父节点，parent变成cur的左
Node* ppNode = parent->_parent;
parent->_parent = SubR;
SubR->_left = parent;
if (ppNode == nullptr)
{
_root = SubR;
_root->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = SubR;
}
else if (ppNode->_right == parent)
{
ppNode->_right = SubR;
}
SubR->_parent = ppNode;
}
parent->_bf = SubR->_bf = 0;
}AVL树分析：
AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1，这
样可以保证查询时高效的时间复杂度，即log_2 N)。
但是如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。因此：如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的(即不会改变)，可以考虑AVL树，但结构经常修改，就不太适合。
红黑树介绍：
红黑树也是一种二叉搜索树，它的结构是接近平衡的。每个节点要么是红色，要么是黑色。通过对任何一条从根到叶子节点的路径上各个节点着色方式的限制，红黑树确保没有一条路径会比其他路径长出两倍，近似平衡，在极端场景下，搜索效率会变成2*log_2 N。
红黑树的性质：
1. 每个结点不是红色就是黑色。
2. 根节点是黑色的。
3. 如果一个节点是红色的，则它的两个孩子结点是黑色的。
4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点。
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点。
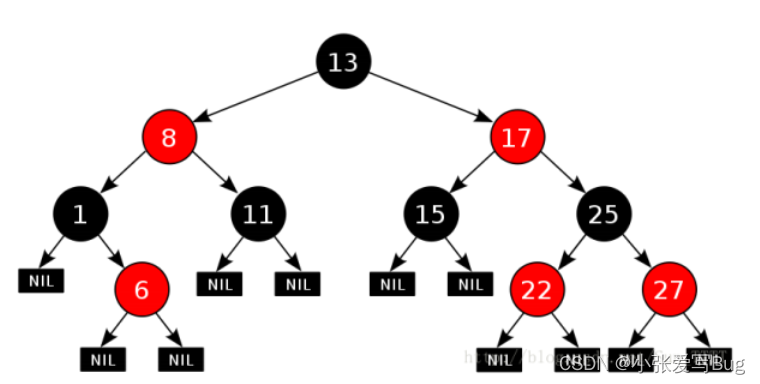
红黑树的插入操作：默认新增节点为红色
1.按照二叉搜索树的方式插入新节点
2.检测新节点插入后，红黑树性质是否遭到破坏
情况1：c为红，p为红，g为黑，u存在且为红。
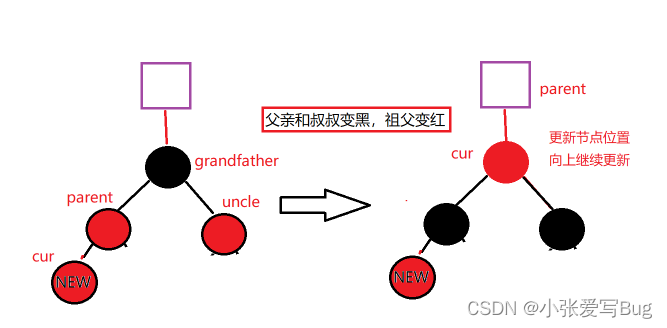
新节点插入后有连续的红节点出现，处理方法：将p,u改为黑，g改为红，然后把g当成cur，继续向上调整。
情况2：c为红，p为红，g为黑，u不存在或者存在且为黑（c/p/g成直线）。
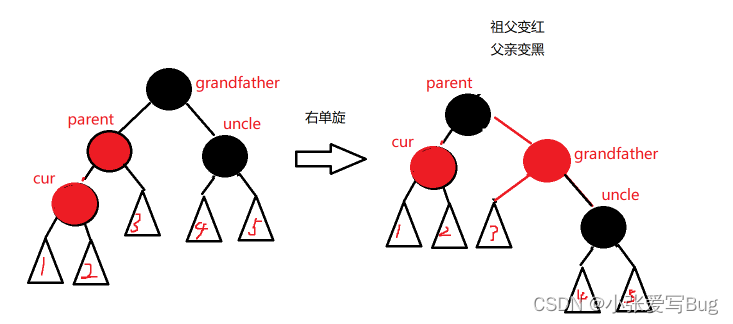p为g的左孩子，cur为p的左孩子，则进行右单旋转；相反，
p为g的右孩子，cur为p的右孩子，则进行左单旋转
p、g变色--p变黑，g变红
情况3：c为红，p为红，g为黑，u不存在或者存在且为黑（c/p/g成一条折线）。
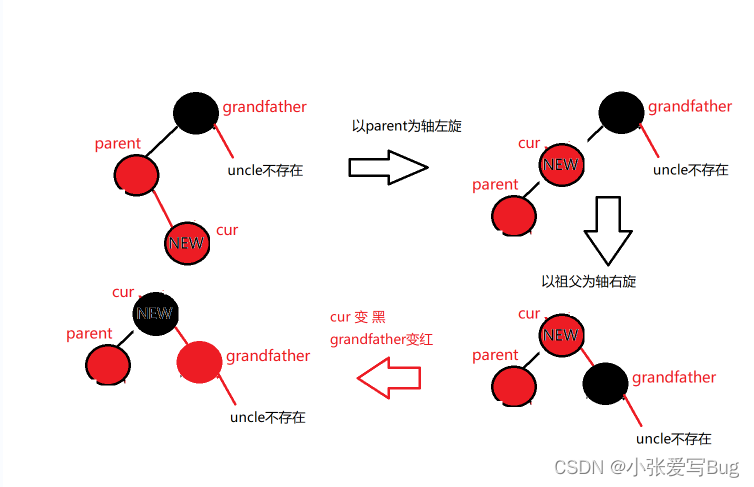p为g的左孩子，cur为p的右孩子，则针对p做左单旋转；相反，
p为g的右孩子，cur为p的左孩子，则针对p做右单旋转
则转换成了情况2，按照情况2进行处理。
红黑树和AVL树对比：
查询效率方面，极端场景下AVL -- log_2 N，红黑树2*log_2 N，AVl树略优。但是由于红黑树不追追求绝对的平衡，降低了旋转次数，在经常需要增删的结构中红黑树更优，实际应用中红黑树更多。
unordered_map/set
unordered_map/set介绍
unordered系列的关联式容器在使用方式上和map/set基本相似，只是底层结构不同。上文提到的红黑树效率在查询时效率可以达到logN，当树中节点非常多的时候，查询效率也不理想。unordered系列容器的底层结构使用的是哈希表，查询效率O(1)。
底层结构：哈希表
构造一种存储结构，通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立
一一映射的关系，那么在查找时通过该函数可以很快找到该元素。
开散列（哈希桶）
开散列法又叫链地址法(开链法)，首先对关键码集合用散列函数计算散列地址，具有相同地
址的关键码归于同一子集合，每一个子集合称为一个桶，各个桶中的元素通过一个单链表链
接起来，各链表的头结点存储在哈希表中。
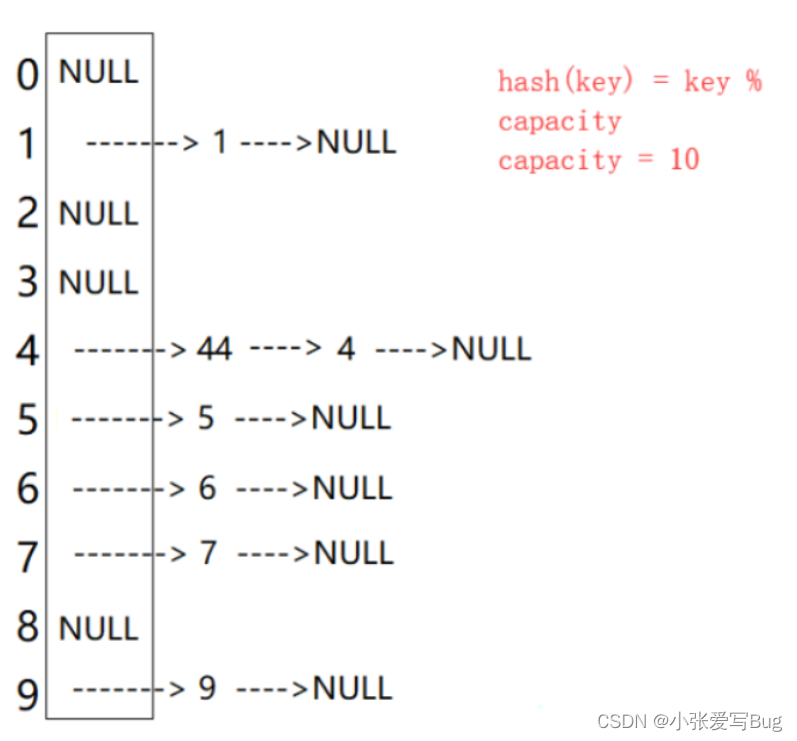
哈希冲突：不同的关键字通过相同的哈希函数计算出相同的哈希地址，该中现象被称为哈希冲突或哈希碰撞。
哈希函数：哈希函数设计的越精妙，产生哈希冲突的可能性就越低，但是无法避免哈希冲突。哈希函数设计原则要注意一下几点：
1.哈希函数的定义域必须包括需要存储的全部关键码，而如果散列表允许有m个地址时，其值
域必须在0到m-1之间。
2.哈希函数计算出来的地址能均匀分布在整个空间中。
3.哈希函数应该比较简单。
直接定址法：取关键字的某个线性函数为散列地址：Hash（Key）= A*Key + B。
优点：简单、均。
缺点：需要事先知道关键字的分布情况。
使用场景：适合查找比较小且连续的情况。
除留余数法：设散列表中允许的地址数为m，取一个不大于m，但最接近或者等于m的质数p作为除数，按照哈希函数：Hash(key) = key% p(p<=m),将关键码转换成哈希地址。
开散列增容：桶的个数是一定的，随着元素的不断插入，每个桶中元素的个数不断增多，极端情况下，可能会导致一个桶中链表节点非常多，会影响的哈希表的性能，因此在一定条件下需要对哈希
表进行增容，那该条件怎么确认呢？开散列最好的情况是：每个哈希桶中刚好挂一个节点，再继续插入元素时，每一次都会发生哈希冲突，因此，在元素个数刚好等于桶的个数时，可以给哈希表增容。
开散列与闭散列比较：应用链地址法处理溢出，需要增设链接指针，似乎增加了存储开销。事实上：由于开地址法必须保持大量的空闲空间以确保搜索效率，如二次探查法要求装载因子a <=
0.7，而表项所占空间又比指针大的多，所以使用链地址法反而比开地址法节省存储空间
知识考察
map和set之间的区别？
1.map存储的是键值对<k，v>,set中只放value,底层存的是<v,v>的键值对。
2.map重载了[],可以通过operator[]进行插入查找，返回值是key对应value的引用，可以对value修改。set的修改方式是先删除这个元素在进行插入。
map和unordered_map之间的区别？
1.底层结构不同，map底层是红黑树，unordered_map的底层是哈希表。
2.unordered_map使用迭代器遍历，得到的数据是无序的，map遍历得到的是有序的序列。
3.一般情况下，unordered_map的查询效率比map更快。
4.从内存存角度来说hash因为底层维护了哈希表的存在，内存消耗远大于红黑树，但是因为哈希表增删查改时的直接映射，使其增删查效率来说可以做到平均O(1),对数据修改较多且不考虑内存问题的场景可以优先考虑hash。
5.红黑树是基于搜索树设计的，具有天然的有序性，hash因为存在哈希冲突所以不能保证存储的数据有序，那么对数据存储存在有序性需求的优先使用红黑树。
一个类型想要做map的key，有什么要求吗？
1.能取模或者配一个仿函数能够转换成整型取模。
2.支持 == 比较。
适配器
stack
stack是一种容器适配器，只能从容器的一端进行元素的插入与提取，后进先出。stack的底层容器可以是任何标准的容器类模板或者一些特定的容器类，这些容器类应该支持如下操作：（empty,back,push_back,pop_back）
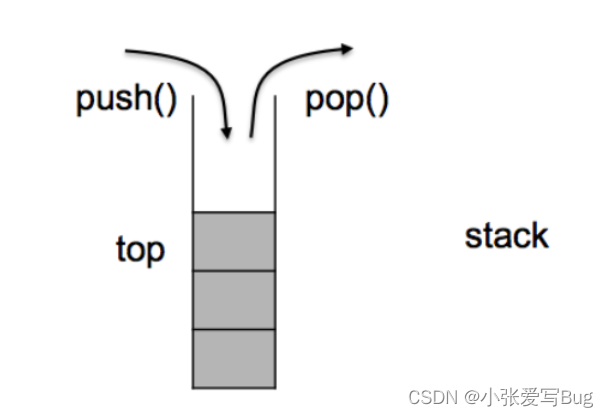
常用接口
empty:检测stack是否为空。
size:返回stack中的元素个数。
top:返回栈顶元素的引用。
push:将元素val压入stack中。
pop:将stack中尾部的元素弹出。
queue
队列是一种元素适配器，容器一端插入元素，另一端提取元素，先进先出。queue其底层容器类可以是标准容器类模板之一，也可以是专门设计的容器类，该底层容器类至少要支持如下操作：
empty、size、front、back、push_back、pop_front。
常用接口使用：
empty：检测队列是否为空。
size：返回队列中有效元素个数。
front：返回队头元素的引用。
back：返回队尾元素的引用。
push： 在队尾将元素入队列。
pop：队头元素出队列。
priority_queue
优先级队列默认使用vector作为其底层存储数据的容器，在vector上又使用了堆算法将vector中元素构造成堆的结构，因此priority_queue就是堆，所有需要用到堆的位置，都可以考虑使用priority_queue。注意：默认情况下priority_queue是大堆。如果想要创建小堆，通过greater改变比较方式。
常用接口：
empty：判断优先级队列是否为空。
top：返回堆顶元素。
push：向优先级队列中插入元素。
pop：删除堆顶元素。
迭代器
什么是迭代器
行为像指针一样的类型。可能是指针，也可能是被封装成的指针，让使用者不用关心容器的底层实现细节，可以用统一的方式轻松访问容器。
迭代器的定义
1.构造函数。
2.具有指针类似的操作，重载operator*和operator->。
3.迭代器要能够比较，重载operator!= 和operator==。
4.迭代器要能够移动，重载operator++()/operator++(int),根据容器的底层数据结构决定是否要支持前置--和后置--。
迭代器失效
1.迭代器指向的位置是不可知的，野指针。
如：vector扩容，导致的野指针问题。list/map删除(erase)节点，导致的野指针问题。
以vector扩容为例
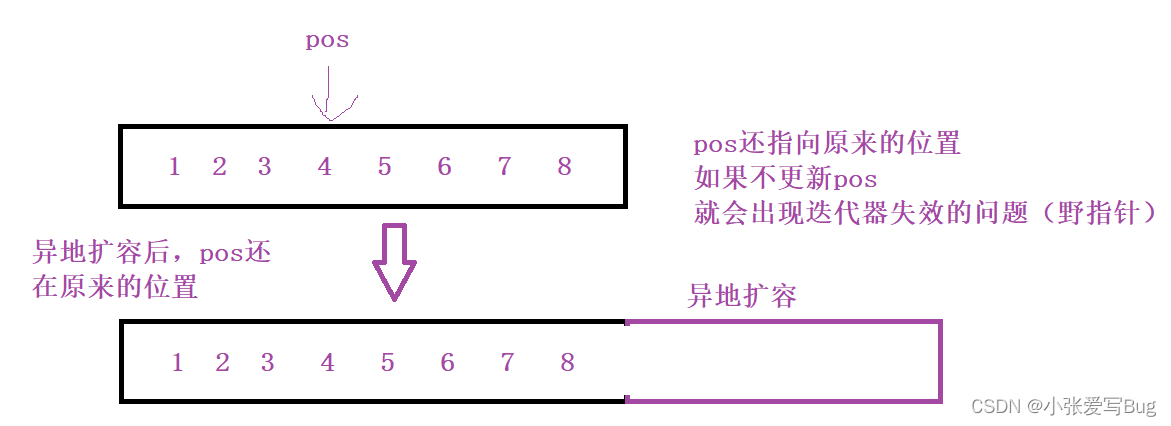
2.迭代器指向的位置已经不在是原来的位置，意义变了。
如:vector不扩容，但是挪动数据（插入或者删除），使迭代器指向的位置已经不是原来的位置。
3.迭代器失效解决办法
在使用前对迭代器重新赋值。
迭代器分类
1.单向迭代器：如forward_list、unordered_map/set。
2.双向迭代器：如map/set、list。
3.随机迭代器：如vector、string。
