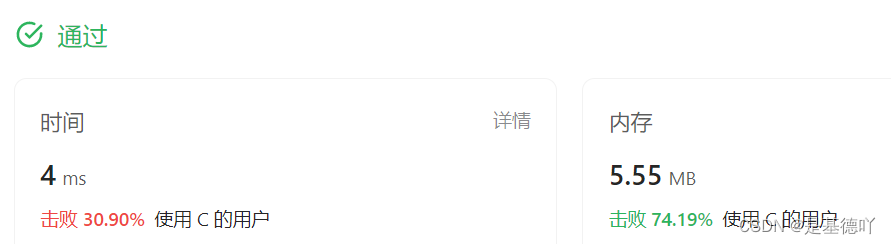
设函数$f(\mathbf{x})$，$\mathbf{x}\in {\text{R}}^n$二阶连续可微，记$\mathbf{g}(\mathbf{x})=\nabla f(\mathbf{x})$，$\mathbf{H}(\mathbf{x})={\nabla }^{2}f(\mathbf{x})$。由于$\mathbf{H}(\mathbf{x})$连续，故${\mathbf{H}}^{\top }(\mathbf{x})=\mathbf{H}(\mathbf{x})$，即$\mathbf{H}(\mathbf{x})$是一个对称矩阵。若$f(\mathbf{x})$有极小值点${\mathbf{x}}_0$，则在${\mathbf{x}}_0$的近旁$\mathbf{H}(\mathbf{x})$是正定的。对具有连续Hesse阵的函数$f(\mathbf{x})$，${\mathbf{x}}_0$近旁点${\mathbf{x}}_k$处的二阶泰勒展开式为
$$f(\mathbf{x})=f({\mathbf{x}}_k)+g_k^{\top }(\mathbf{x}-{\mathbf{x}}_k)+\frac{1}{2}(\mathbf{x}-{\mathbf{x}}_k{)}^{\top }{\mathbf{H}}_k(\mathbf{x}-{\mathbf{x}}_k)+o(\Vert \mathbf{x}-{\mathbf{x}}_k\Vert ).$$
其中，${\mathbf{g}}_k=\nabla f({\mathbf{x}}_k)$，${\mathbf{H}}_k=\mathbf{H}({\mathbf{x}}_k)={\nabla }^{2}f({\mathbf{x}}_k)$。令
$$q_k(\mathbf{x})=f({\mathbf{x}}_k)+{\mathbf{g}}_k^{\top }(\mathbf{x}-{\mathbf{x}}_k)+\frac{1}{2}(\mathbf{x}-{\mathbf{x}}_k{)}^{\top }{\mathbf{H}}_k(\mathbf{x}-{\mathbf{x}}_k)$$
则$q_k({\mathbf{x}}_k)=f({\mathbf{x}}_k)$，$\nabla q_k({\mathbf{x}}_k)=\nabla f({\mathbf{x}}_k)$，${\nabla }^2{q}_k({\mathbf{x}}_k)={\nabla }^{2}f({\mathbf{x}}_k)$。因此当$\mathbf{x}$在${\mathbf{x}}_k$近旁时，可用二次型函数$q_k(\mathbf{x})$作为$f(\mathbf{x})$的近似表示。由${\nabla }^2{q}_k({\mathbf{x}}_k)={\nabla }^{2}f({\mathbf{x}}_k)={\mathbf{H}}_k$的正定性知二次型函数$q_k(\mathbf{x})$有唯一最小值点。由于$q_k(\mathbf{x})$二阶连续可微，故其最小值点必为其驻点：$\mathbf{o}=q_k^{\prime }(\mathbf{x})=\nabla q_k(\mathbf{x})=\nabla f({\mathbf{x}}_k)+{\nabla }^{2}f({\mathbf{x}}_k)(\mathbf{x}-{\mathbf{x}}_k)={\mathbf{g}}_k+{\mathbf{H}}_k\mathbf{x}-{\mathbf{H}}_k{\mathbf{x}}_k$。即$q_k(\mathbf{x})$的驻点${\mathbf{x}}_{k+1}$满足
$${\mathbf{H}}_k{\mathbf{x}}_{k+1}={\mathbf{H}}_k{\mathbf{x}}_k-{\mathbf{g}}_k.$$
由${\mathbf{H}}_k$的正定性知${\mathbf{H}}_k$可逆，故由上式可解得$q_k(\mathbf{x})$的最小值点（如下图所示）
$${\mathbf{x}}_{k+1}={\mathbf{x}}_k-{\mathbf{H}}_k^{-1}{\mathbf{g}}_k.(1)$$

在对目标函数$f(\mathbf{x})$如上描述的条件下，式(1)构成搜索$f(\mathbf{x})$的最优解${\mathbf{x}}_0$的迭代式：初始时，在${\mathbf{x}}_0$的近旁任取点${\mathbf{x}}_1$，此时可保证$f(\mathbf{x})$在${\mathbf{x}}_1$处的Hesse阵${\mathbf{H}}_1={\nabla }^{2}f({\mathbf{x}}_1)$是正定的。若${\mathbf{x}}_1={\mathbf{x}}_0$，则得到了最优解${\mathbf{x}}_1={\mathbf{x}}_0$。否则按式(3.9)可算得点${\mathbf{x}}_2={\mathbf{x}}_1-{\mathbf{H}}_1^{-1}{\mathbf{g}}_k$。由于${\mathbf{x}}_2$是$q_1(\mathbf{x})$的最小值点，故$q_1(\mathbf{x})$从${\mathbf{x}}_1$到${\mathbf{x}}_2$函数值是下降的。由$f(\mathbf{x})$与$q_1(\mathbf{x})$在${\mathbf{x}}_1$处的相近性可知$f(\mathbf{x})$从${\mathbf{x}}_1$到${\mathbf{x}}_2$函数值也是下降的，故可望${\mathbf{x}}_2$比${\mathbf{x}}_1$更接近${\mathbf{x}}_0$。若$\nabla f({\mathbf{x}}_2)=\mathbf{o}$，则按$f(\mathbf{x})$所具有的
单峰性知，我们得到了最优解${\mathbf{x}}_2={\mathbf{x}}_0$。否则，可由式(1)计算${\mathbf{x}}_3$，……，按此方式算得点${\mathbf{x}}_k$，且${\mathbf{x}}_k$位于${\mathbf{x}}_0$的近旁。若此时$\nabla f({\mathbf{x}}_k)=\mathbf{o}$，则得到最优解${\mathbf{x}}_k={\mathbf{x}}_0$。否则，可由式(1)算得更接近${\mathbf{x}}_0$的点${\mathbf{x}}_{k+1}={\mathbf{x}}_k-{\mathbf{H}}_k^{-1}{\mathbf{g}}_k$，如上图所示。用这样的方法计算目标函数最优解的迭代序列算法称为牛顿法。
下列代码实现牛顿算法。

import numpy as np                          #导入numpy
from scipy.optimize import OptimizeResult   #导入OptimizeResult
def newton(f, x1, gtol, **options):
    xk=x1
    gk=grad(f,xk)
    Hk=hess(f,xk)
    k=1
    while np.linalg.norm(gk)>=gtol:
        xk-=np.matmul(np.linalg.inv(Hk),gk)
        gk=grad(f,xk)
        Hk=hess(f,xk)
        k+=1
    bestx=xk
    besty=f(bestx)
    return OptimizeResult(fun=besty, x=bestx, nit=k)

程序的第3~15行定义的newton函数实现牛顿算法。参数f，x1，gtol分别表示目标函数$f(\mathbf{x})$，初始点${\mathbf{x}}_1$和容错误差$\epsilon$，options实现minimize与本函数的信息交换机制。
第4~7行执行初始化操作：第4行将表示迭代点的xk初始化为x1。第5、6行分别调用函数grad和hess（详见博文《最优化方法Python计算：n元函数梯度与Hesse阵的数值计算》）计算目标函数$f(\mathbf{x})$在当前点${\mathbf{x}}_1$处的梯度$\nabla f({\mathbf{x}}_1)$和Hesse矩阵${\nabla }^{2}f({\mathbf{x}}_1)$，赋予gk和Hk。第7行将迭代次数k初始化为1。
第8~12行的while循环执行迭代操作：第9行按式(1)
$${\mathbf{x}}_{k+1}={\mathbf{x}}_k-{\mathbf{H}}_k^{-1}{\mathbf{g}}_k$$
计算迭代点更新xk。其中调用numpy.linalg的inv函数计算$\mathbf{H}$的逆矩阵${\mathbf{H}}_k^{-1}$，调用numpy的matmul函数计算矩阵的积${\mathbf{H}}_k^{-1}{\mathbf{g}}_k$。第10、11行调用grad函数和hess函数计算$\nabla f({\mathbf{x}}_{k+1})$和Hesse矩阵${\nabla }^{2}f({\mathbf{x}}_{k+1})$更新gk和Hk。第12行将迭代次数k自增1。循环往复，直至条件
$$\Vert {\mathbf{g}}_k\Vert <\epsilon$$
成立为止。
第13~15行用$f({\mathbf{x}}_k)$，${\mathbf{x}}_k$及$k$构造OptimizeResult（第2行导入）对象并返回。
例1 给定$\epsilon =10^{-8}$为容错误差，分别以$\left(\begin{array}{c}0\\ 0\end{array}\right)$和$\left(\begin{array}{c}-1.2\\ 1\end{array}\right)$作为初始点${\mathbf{x}}_1$，用newton函数计算Rosenbrock函数的最优解。
解：下列代码完成计算。

import numpy as np                                              #导入numpy
from scipy.optimize import minimize, rosen                      #导入minimize, rosen
x1=np.array([0,0])                                              #设置初始点
res=minimize(rosen, x1,method=newton, options={'gtol':1e-8})    #计算最优解
print(res)
x1=np.array([-1.2,1])                                           #设置初始点
res=minimize(rosen, x1,method=newton, options={'gtol':1e-8})    #计算最优解
print(res)

程序的第3~ 4行及第6~7行分别以$\left(\begin{array}{c}0\\ 0\end{array}\right)$和$\left(\begin{array}{c}-1.2\\ 1\end{array}\right)$作为初始点${\mathbf{x}}_1$调用minimize传递newton计算Rosenbrock函数容错误差为$10^{-8}$的最优解近似值。运行程序，输出

 fun: 6.156132219000243e-22
 nit: 7
   x: array([1., 1.])
 fun: 1.4934237207405332e-18
 nit: 11
   x: array([1., 1.])

前3行表示从${\mathbf{x}}_1=\left(\begin{array}{c}0\\ 0\end{array}\right)$起，迭代7次，newton算得最优解$\left(\begin{array}{c}1\\ 1\end{array}\right)$，后3行则表示newton从${\mathbf{x}}_1=\left(\begin{array}{c}-1.2\\ 1\end{array}\right)$起，迭代11次，算得最优解。读者可以相同起点及容错误差用FR共轭梯度算法计算Rossenbrock函数的最优解的结果相比较，将看到牛顿算法比FR共轭梯度法（详见博文《最优化方法Python计算：非二次型共轭梯度算法》）计算（对两个不同的初始点，在相同的容错误差下分别迭代24次和20次）效率更高。