一、说明
在这个由 4 部分组成的系列中,我们将使用 PyTorch 中的深度学习技术从头开始逐步实现图像分割。本部分将重点介绍如何使用深度可分离卷积来优化我们的 CNN 基线模型,以减少可训练参数的数量,使模型可部署在移动设备和其他边缘设备上。

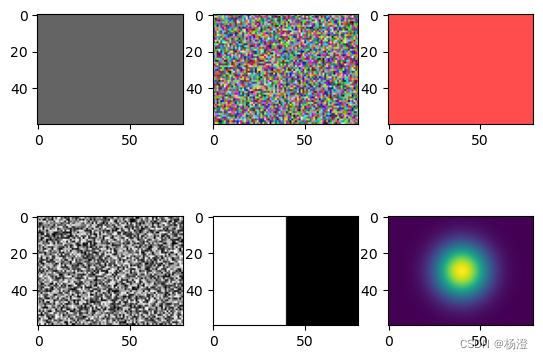
图 1:使用具有深度可分离卷积而不是常规卷积的 CNN 运行图像分割的结果。从上到下,输入图像、地面实况分割掩码和预测分割掩码。
二、文章大纲
在本文中,我们将增强我们之前构建的卷积神经网络(CNN),以减少网络中可学习参数的数量。在输入图像中识别宠物像素(属于猫、狗、仓鼠等的像素)的任务保持不变。我们选择的网络仍将是SegNet,我们唯一要做的改变是用深度可分离卷积(DSC)替换我们的卷积层。在我们这样做之前,我们将深入研究深度可分离卷积的理论和实践,并欣赏该技术背后的想法。
在本文中,我们将参考此笔记本中的代码和结果进行模型训练,并引用此笔记本中的代码和结果进行 DSC 入门。如果要重现结果,则需要一个 GPU 来确保第一个笔记本在合理的时间内完成运行。第二个笔记本可以在常规 CPU 上运行。
三、本系列文章
本系列面向所有深度学习经验水平的读者。如果您想了解深度学习和视觉AI的实践以及一些扎实的理论和实践经验,那么您来对地方了!这将是一个由 4 部分组成的系列,包含以下文章:
- 概念和想法
- 基于 CNN 的模型
- 深度可分离卷积(本文)
- 基于视觉变压器的模型
四、介绍
让我们从模型大小和计算成本的角度仔细研究卷积开始讨论。可训练参数的数量可以很好地指示模型的大小,张量运算的数量反映了模型的复杂性或计算成本。考虑我们有一个卷积层,其中包含 n 个大小为 dk x dk 的过滤器。进一步假设该层处理形状为 m x h x w 的输入,其中 m 是输入通道的数量,h 和 w 分别是高度和宽度尺寸。在这种情况下,卷积层将产生形状为 n x h x w 的输出,如图 2 所示。我们假设卷积使用 stride=1。让我们继续根据可训练参数和计算成本来评估此设置。

图 2:应用于输入以产生输出的常规卷积滤波器。假设步幅=1,填充=dk-2。来源:高效深度学习书
可训练参数的评估:我们有 n 个过滤器,每个过滤器都有 m x dk x dk 可学习参数。这导致总共有 n x m x dk x dk 可学习参数。忽略偏见术语以简化此讨论。让我们看看下面的 PyTorch 代码来验证我们的理解。
import torch
from torch import nn
def num_parameters(m):
return sum([p.numel() for p in m.parameters()])
dk, m, n = 3, 16, 32
print(f"Expected number of parameters: {m * dk * dk * n}")
conv1 = nn.Conv2d(in_channels=m, out_channels=n, kernel_size=dk, bias=False)
print(f"Actual number of parameters: {num_parameters(conv1)}")打印以下内容。
Expected number of parameters: 4608
Actual number of parameters: 4608现在,让我们评估卷积的计算成本。
计算成本评估:当在大小为 h x w 的输入上以步幅=1 和填充 = dk-2 运行时,形状为 m x dk x dk 的单个卷积过滤器将应用卷积过滤器 h x w 次,对于大小为 dk x dk 的每个图像部分总共应用 h x w 部分一次。它导致每个滤波器或输出通道的成本为 m x dk x dk x h x w。由于我们希望计算 n 个输出通道,因此总成本将为 m x dk x dk x h x n。让我们继续使用torchinfo PyTorch包来验证这一点。
from torchinfo import summary
h, w = 128, 128
print(f"Expected total multiplies: {m * dk * dk * h * w * n}")
summary(conv1, input_size=(1, m, h, w))将打印以下内容。
Expected total multiplies: 75497472
==========================================================================================
Layer (type:depth-idx) Output Shape Param #
==========================================================================================
Conv2d [1, 32, 128, 128] 4,608
==========================================================================================
Total params: 4,608
Trainable params: 4,608
Non-trainable params: 0
Total mult-adds (M): 75.50
==========================================================================================
Input size (MB): 1.05
Forward/backward pass size (MB): 4.19
Params size (MB): 0.02
Estimated Total Size (MB): 5.26
==========================================================================================如果我们暂时忽略卷积层的实现细节,我们会意识到,在高层次上,卷积层只是将 m x h x w 输入转换为 n x h x w 输出。转换是通过可训练的过滤器实现的,这些过滤器在看到输入时逐渐学习特征。接下来的问题是:是否有可能使用更少的可学习参数来实现这种转换,同时确保层的学习能力的最小妥协?提出了深度可分卷积来回答这个确切的问题。让我们详细了解它们,并了解它们在我们的评估指标上是如何叠加的。
五、深度可分离卷积
深度可分卷积(DSC)的概念最初是由Laurent Sifre在他们的博士论文“用于图像分类的刚性运动散射”中提出的。从那时起,它们已成功用于各种流行的深度卷积网络,如XceptionNet和MobileNet。
常规卷积和 DSC 之间的主要区别在于 DSC 由 2 个卷积组成,如下所述:
- 深度分组卷积,其中输入通道数 m 等于输出通道数,使得每个输出通道仅受单个输入通道的影响。在 PyTorch 中,这被称为“分组”卷积。您可以在此处阅读有关 PyTorch 中分组卷积的更多信息。
- 逐点卷积(滤波器大小=1),其操作类似于常规卷积,因此n个滤波器中的每个都在所有m个输入通道上运行以产生单个输出值。

图 3:应用于输入以产生输出的深度可分离卷积滤波器。假设步幅=1,填充=dk-2。来源:高效深度学习书
让我们执行与 DSC 常规卷积相同的练习,并计算可训练参数和计算的数量。
可训练参数的评估:“分组”卷积有 m 个滤波器,每个滤波器都有 dk x dk 可学习参数,可生成 m 个输出通道。这导致总共 m x dk x dk 可学习参数。逐点卷积有 n 个大小为 m x 1 x 1 的过滤器,其加起来最多有 n x m x 1 x 1 个可学习参数。让我们看看下面的 PyTorch 代码来验证我们的理解。
class DepthwiseSeparableConv(nn.Sequential):
def __init__(self, chin, chout, dk):
super().__init__(
# Depthwise convolution
nn.Conv2d(chin, chin, kernel_size=dk, stride=1, padding=dk-2, bias=False, groups=chin),
# Pointwise convolution
nn.Conv2d(chin, chout, kernel_size=1, bias=False),
)
conv2 = DepthwiseSeparableConv(chin=m, chout=n, dk=dk)
print(f"Expected number of parameters: {m * dk * dk + m * 1 * 1 * n}")
print(f"Actual number of parameters: {num_parameters(conv2)}")这将打印。
Expected number of parameters: 656
Actual number of parameters: 656我们可以看到 DSC 版本的参数大约减少了 7 倍。接下来,让我们将注意力集中在 DSC 层的计算成本上。
计算成本评估:假设我们的输入具有空间维度 m x h x w。在DSC的分组卷积段中,我们有m个过滤器,每个过滤器的大小为dk x dk。滤波器应用于其相应的输入通道,导致段成本为 m x dk x dk x h x w。对于逐点卷积,我们应用 n 个大小为 m x 1 x 1 的滤波器来产生 n 个输出通道。这导致段成本为 n x m x 1 x 1 x h x w。我们需要将分组和逐点操作的成本相加以计算总成本。让我们继续使用torchinfo PyTorch包来验证这一点。
print(f"Expected total multiplies: {m * dk * dk * h * w + m * 1 * 1 * h * w * n}")
s2 = summary(conv2, input_size=(1, m, h, w))
print(f"Actual multiplies: {s2.total_mult_adds}")
print(s2)这将打印。
Expected total multiplies: 10747904
Actual multiplies: 10747904
==========================================================================================
Layer (type:depth-idx) Output Shape Param #
==========================================================================================
DepthwiseSeparableConv [1, 32, 128, 128] --
├─Conv2d: 1-1 [1, 16, 128, 128] 144
├─Conv2d: 1-2 [1, 32, 128, 128] 512
==========================================================================================
Total params: 656
Trainable params: 656
Non-trainable params: 0
Total mult-adds (M): 10.75
==========================================================================================
Input size (MB): 1.05
Forward/backward pass size (MB): 6.29
Params size (MB): 0.00
Estimated Total Size (MB): 7.34
========================================================================================== 让我们比较两个卷积的大小和成本,举几个例子来获得一些直觉。
六、常规和深度可分离卷积的尺寸和成本比较
为了比较常规卷积和深度可分离卷积的大小和成本,我们将假设网络的输入大小为 128 x 128,内核大小为 3 x 3,以及一个逐渐将空间维度减半并将通道维度数量加倍的网络。我们假设每一步都有一个 2D-conv 层,但实际上,可能还有更多。

图 4:比较常规和深度可分离卷积的可训练参数(大小)和多加(成本)的数量。我们还显示了 2 种卷积的大小和成本之比。资料来源:作者。
您可以看到,平均而言,DSC 的大小和计算成本约为上述配置常规卷积成本的 11% 到 12%。

图 5:常规 VS/s DSC 的相对大小和成本。资料来源:作者。
现在我们已经对卷积的类型及其相对成本有了很好的了解,你一定想知道使用 DSC 是否有任何缺点。 到目前为止,我们所看到的一切似乎都表明它们在各个方面都更好!好吧,我们还没有考虑一个重要的方面,即它们对我们模型准确性的影响。让我们通过下面的实验深入了解它。
七、使用深度可分离卷积的SegNet
此笔记本包含此部分的所有代码。
我们将调整上一篇文章中的SegNet模型,并用DSC层替换所有常规卷积层。完成此操作后,我们注意到笔记本中的参数数量从 15.27M 下降到 1.75M,减少了 88.5%!这与我们之前估计的网络可训练参数数量减少 11% 到 12% 一致。
在模型训练和验证期间使用了与以前类似的配置。配置指定如下。
- 随机水平翻转和颜色抖动数据增强应用于训练集以防止过度拟合
- 在非宽高比保留调整大小操作中将图像大小调整为 128x128 像素
- 不会对图像应用任何输入归一化,而是使用批量归一化层作为模型的第一层
- 该模型使用 LR 为 20.0 且没有 LR 调度程序的 Adam 优化器训练了 001 个 epoch
- 交叉熵损失函数用于将像素分类为属于宠物、背景或宠物边框
该模型在 86 个训练周期后实现了 96.20% 的验证准确率。这低于模型在相同数量的训练周期内使用常规卷积所达到的 88.28% 的准确率。我们已经通过实验确定,训练更多的 epoch 可以提高两个模型的准确性,所以 20 个 epoch 绝对不是训练周期的结束。出于本文的目的,我们停在 20 个纪元,以便进行演示。
我们绘制了一个 gif,显示了模型如何学习预测验证集中 21 张图像的分割掩码。

图 6:一个 gif,显示了带有 DSC 的 SegNet 模型如何学习预测验证集中 21 张图像的分割掩码。来源:作者
现在我们已经了解了模型在训练周期中是如何进展的,让我们将模型的训练周期与常规卷积和 DSC 进行比较。
八、精度比较
我们发现使用常规卷积和DSC查看模型的训练周期很有用。我们注意到的主要区别是在训练的早期阶段(时期),之后两个模型大致进入相同的预测流。事实上,在训练了两个模型 100 个 epoch 之后,我们注意到使用 DSC 的模型的精度仅比具有常规卷积的模型低约 1%。这与我们对20个训练时期的观察结果一致。

图 7:一个 gif,显示了 SegNet 模型使用常规卷积与 DSC 预测的分割掩码的进展。资料来源:作者。
你会注意到,两个模型在仅仅 6 个训练周期后就大致正确地得到了预测——也就是说,人们可以直观地看到模型正在预测一些有用的东西。然后,训练模型的大部分艰苦工作都在确保预测的面具的边界尽可能紧密,并尽可能接近图像中的实际宠物。这意味着,虽然人们可以预期在后期训练时期准确性的绝对提高较小,但这对预测质量的影响要大得多。我们注意到,在更高的绝对准确度值(从 89% 到 90%)下,准确度提高个位数会导致预测的显著定性改进。
九、与联合国网络模式的比较
我们进行了一项实验,更改了许多超参数,重点是提高整体准确性,以了解此设置离接近最佳有多远。下面是该实验的配置。
- 图像尺寸:128 x 128 — 与迄今为止的实验相同
- 训练周期:100 — 当前实验训练了 20 个周期
- 增强:更多的增强,例如图像旋转,通道丢弃,随机块删除。我们使用Albumentations而不是Torchvision转换。蛋白为我们自动转换分割掩码
- LR 调度器:使用 StepLR 调度器,每 0 个列车周期衰减 8.25 倍
- 损失函数:我们尝试了 4 种不同的损失函数:交叉熵、焦点、骰子、加权交叉熵。骰子表现最差,而其余的几乎可以相互媲美。事实上,100 个 epoch 之后其余部分之间的最佳精度差异在小数点后的第 4 位(假设精度是 0.0 到 1.0 之间的数字)
- 卷积类型:常规
- 模型类型:UNet — 当前实验使用SegNet模型
对于上述设置,我们实现了91.3%的最佳验证准确率。我们注意到图像大小会显著影响最佳验证精度。例如,当我们将图像大小更改为 256 x 256 时,最佳验证准确度高达 93.0%。但是,训练花费的时间要长得多,并且使用更多的内存,这意味着我们必须减小批量大小。

图 8:使用上述超参数训练 100 个训练时期的 UNet 模型的结果。资料来源:作者。
您可以看到,与我们迄今为止看到的预测相比,预测更加平滑和清晰。
十、结论
在本系列的第 3 部分中,我们了解了深度可分离卷积 (DSC) 作为一种在不显著降低验证准确性的情况下减小模型大小和训练/推理成本的技术。我们了解了特定设置在常规和 DSC 之间的大小/成本权衡。
我们展示了如何调整SegNet模型以在PyTorch中使用DSC。这种技术可以应用于任何深度CNN。事实上,我们可以有选择地用DSC替换一些卷积层——也就是说,我们不一定需要替换所有卷积层。选择要替换的图层将取决于您希望在模型大小/运行时成本和预测精度之间取得的平衡。此决定将取决于您的特定用例和部署设置。
虽然本文训练了 20 个 epoch 的模型,但我们解释说这对于生产工作负载来说是不够的,并提供了一瞥如果为更多 epoch 训练模型可以期待什么。此外,我们还介绍了一些可以在模型训练期间调整的超参数。虽然此列表并不全面,但它应该可以让您了解为生产工作负载训练图像分割模型所需的复杂性和决策。