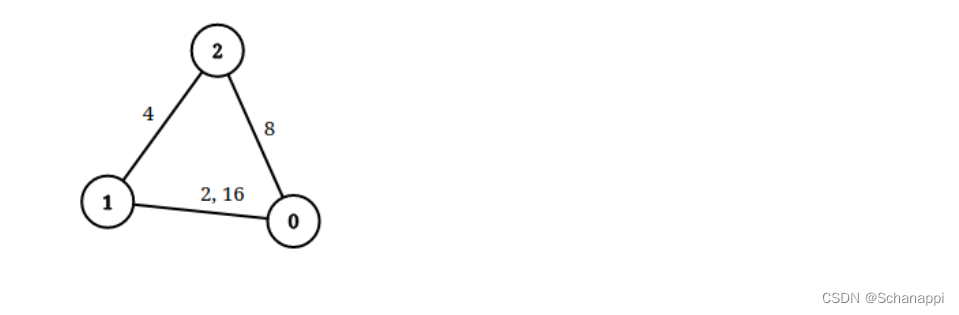题目描述
给你一个 n 个点组成的无向图边集 edgeList ,其中 edgeList[i] = [ui, vi, disi] 表示点 ui 和点 vi 之间有一条长度为 disi 的边。请注意,两个点之间可能有 超过一条边 。
给你一个查询数组queries ,其中 queries[j] = [pj, qj, limitj] ,你的任务是对于每个查询 queries[j] ,判断是否存在从 pj 到 qj 的路径,且这条路径上的每一条边都 严格小于 limitj 。
请你返回一个 布尔数组 answer ,其中 answer.length == queries.length ,当 queries[j] 的查询结果为 true 时, answer 第 j 个值为 true ,否则为 false 。示例 1:
输入:n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
输出:[false,true]
解释:上图为给定的输入数据。注意到 0 和 1 之间有两条重边,分别为 2 和 16 。
对于第一个查询,0 和 1 之间没有小于 2 的边,所以我们返回 false 。
对于第二个查询,有一条路径(0 -> 1 -> 2)两条边都小于 5 ,所以这个查询我们返回 true 。示例 2:
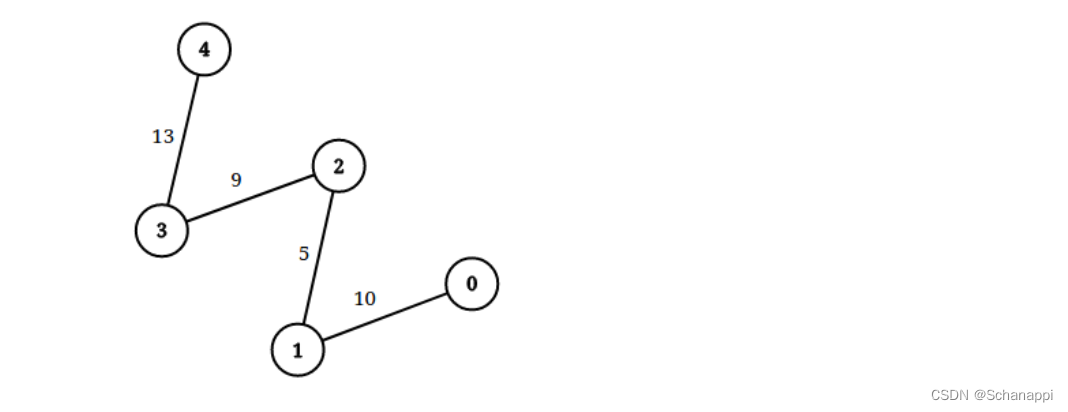
输入:n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
输出:[true,false]
解释:上图为给定数据。提示:
2 <= n <= 105
1 <= edgeList.length, queries.length <= 105
edgeList[i].length == 3
queries[j].length == 3
0 <= ui, vi, pj, qj <= n - 1
ui!= vi
pj != qj
1 <= disi, limitj <= 109
两个点之间可能有 多条 边。
方法一:并查集+离线思维
思路:
- 将 queries 按照 limitj 从小到大进行排序,这样所有的询问中对边权的限制就 单调递增 了;
- 同时,将 edgeList 按照 disj 从小到大排序,这样所有的边权也就 单调递增 了;
- 使用 并查集 维护图的连通性,并使用指针 i 表示当前并查集中添加的最后一条边;
- 当我们处理到询问 queriesj = (pj , qj, limitj) 时,由于 limitj 单调递增,因此只需要往并查集中添加新的边,即不断地在 edgeList 中向右移动指针 i ,直到当前指向的边权 disi >= limitj 为止;
- 随后只需要使用并查集判断 pj 和 qj 是否连通即可。
情况
- 通过;
收获
- 这道题看了一下感觉会用到图的知识,这一块我很薄弱,就直接看题解了,没想到比图还更难;
- 「离线思维」
对于一道题目会给出若干询问,而这些询问是全部提前给出的,也就是说,不必按照询问的顺序依次对它们进行处理,而是可以按照某种顺序或者把所有询问看成一个整体处理。- 「并查集」
一种树形的数据结构,用于处理集合的合并和查询问题,支持两种操作:
- 查找(Find):确定某个元素处于哪个子集;该操作会用到路径压缩。
- 合并(Union):将两个子集合并成一个集合;
代码中包含并查集模板;
- 将 queries 和 edgeList 进行排序的巧妙之处,在于我们实际上进行了这样的操作:
- 将所有的 queries 和 edgeList 合并,并按照边权或者边权限制进行排序。在出现相等的情况时, queries 或者 edgeList 内部的相对顺序并不重要,但所有的 queries 必须要排在所有的 edgeList 之前,这是因为题目中要求对于每一个询问,经过的边权都是严格小于边权限制的;
- 在排序之后,我们依次遍历所有元素。如果当前元素是 queries ,我们就使用并查集进行查询操作,如果当前元素是 edgeList ,就使用并查集进行修改操作。
- 「对下标数组进行排序」
这一题中没有直接对 queries 进行排序,因为如果这么做会导致答案数组和 queries 的原来顺序对不上。因此使用 iota 函数(自加函数) 生成一个从 0 开始的 下标数组 ,对 qid下标数组进行排序,使得顺序取 qid 数组的值作为下标来访问 queries 数组,就是对 queries 数组的升序访问。
这一种方法适用于 对答案有特殊顺序要求 或 不方便对原来数组直接进行排序 的情况。时间复杂度:O(m logm + q logq),其中 m 和 q 分别是数组 edgeList 和 queries 的长度,时间复杂度的瓶颈在于排序;
空间复杂度:O(n + logm + q),其中O(n) 为并查集, O(logm)为数组 edgeList 排序使用的栈空间,O(q)为存储所有询问的编号,对应排序中O(logq)的栈空间,可以忽略。
// 并查集模板,包含路径压缩以及按秩合并
class UF{
public:
vector<int> fa; // 存储每个点的父节点,初始时每个点的父节点都是它本身
vector<int> sz; // 只有节点是祖宗节点时才有意义,表示祖宗节点所在集合中点的数量
int n; // 节点数
int comp_cnt;
public:
// 有参数的构造函数
UF(int _n): n(_n), comp_cnt(_n), fa(_n), sz(_n, 1){
// iota:自增函数,fa=[0,1,2,3,...]
iota(fa.begin(), fa.end(), 0);
}
// 寻找元素x的集合的祖宗节点
int findset(int x){
return fa[x] == x ? x : fa[x] = findset(fa[x]);
// 路径压缩:
// fa[x] = findset(fa[x])
}
bool unite(int x, int y){
x = findset(x);
y = findset(y);
if(x == y){
// 两个元素在同一个集合中,无需合并
return false;
}
// 合并x和y
// 确保x是秩大的元素
if(sz[x] < sz[y]){
swap(x, y);
}
fa[y] = x; // 将y加入集合x
sz[x] += sz[y]; // 更新x的秩
-- comp_cnt;
return true;
}
// 判断x和y是否连通
bool connected(int x, int y){
x = findset(x);
y = findset(y);
// 如果x和y在一个集合中,表示连通
return x == y;
}
};
class Solution{
public:
vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {
vector<int> qid(queries.size());
// 创建0 - (n-1) 的数组
iota(qid.begin(), qid.end(), 0);
// 将queries按照边权限制从小到大排序
// [&]:以引用形式捕获所有外部变量,也就是外部变量均可用
sort(qid.begin(), qid.end(), [&](int i, int j){
return queries[i][2] < queries[j][2];
});
// 将edgeList按照从小到大排序
sort(edgeList.begin(), edgeList.end(), [](const auto& e1, const auto& e2){
return e1[2] < e2[2];
});
// 并查集
UF uf(n);
int i = 0;
vector<bool> ans(queries.size());
for(int query : qid){
// 往并查集中添加元素,直到边权关系 dis_i < limit_j 不满足
while(i < edgeList.size() && edgeList[i][2] < queries[query][2]){
uf.unite(edgeList[i][0], edgeList[i][1]);
++ i;
}
// 使用并查集判断连通性
ans[query] = uf.connected(queries[query][0], queries[query][1]);
}
return ans;
}
};
参考资料
- c++ iota()函数