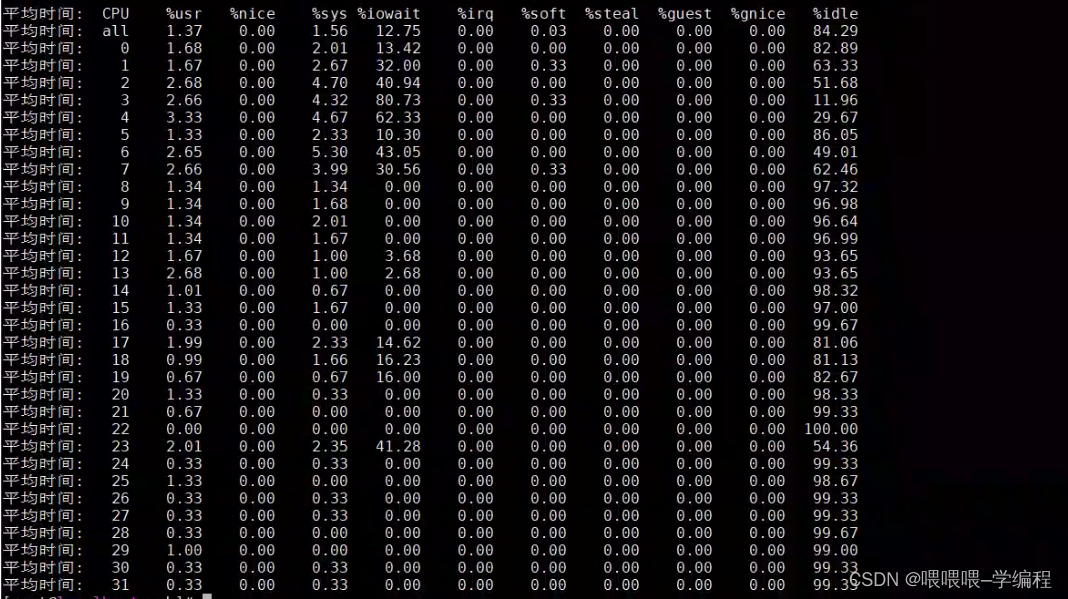
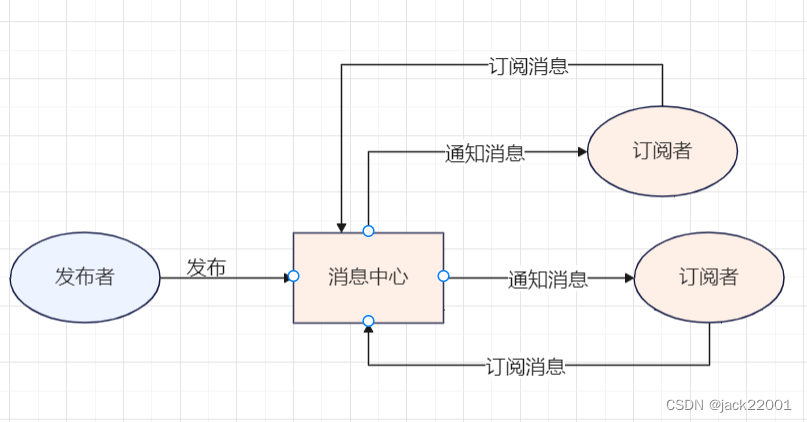
自注意力是注意力机制的一种特殊情况,其核心思想为通过计算特征内部元素之间的联系来获得大范围内的依赖关系。而在外部注意力中,key被拿到了网络外部,因此可以习得数据集的全局状况。
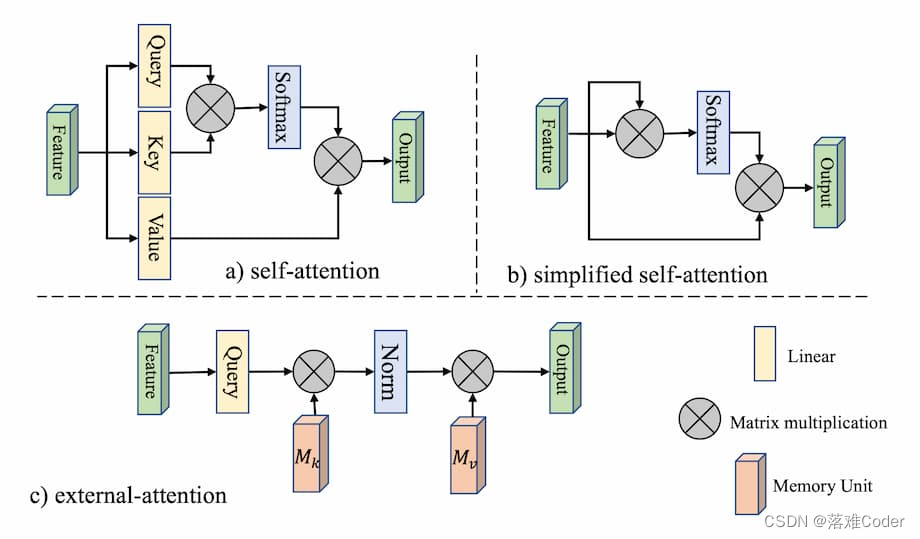
自注意力机制中,输入特征F被投射到query矩阵Q、key矩阵K与value矩阵V中。之后注意力可记为
A
=
(
α
)
i
,
j
=
softmax
(
Q
K
T
)
A=(\alpha)_{i,j}=\text{softmax}(QK^T)
A=(α)i,j=softmax(QKT) 。另外一种简化的变体则直接计算注意力
A
=
(
α
)
i
,
j
=
softmax
(
F
F
T
)
A=(\alpha)_{i,j}=\text{softmax}(FF^T)
A=(α)i,j=softmax(FFT) 。然而,简化之后计算复杂度
O
(
d
N
2
)
O(dN^2)
O(dN2) 过高的问题依然存在。作者在检视注意力图之后发现大部分像素其实只与少数像素之间存在较强联系。因此N×N的注意力矩阵存在冗余。最终优化后的特征计算仅需要特定的数值即可。为此作者提出了外部注意力模块,计算输入像素与外部的记忆矩阵单元M之间的注意力。此时的注意力变为:
A = ( α ) i , j = Norm ( F M T ) A =(\alpha)_{i,j}= \text{Norm}(FM^T ) A=(α)i,j=Norm(FMT)
与自注意力不同的是,上式中的 ( α ) i , j (\alpha)_{i,j} (α)i,j 代表了第i个像素与M的第j行。这里的M为一个与输入无关的可学习参数,作为数据集相关的记忆器。实际中,作者使用了两个记忆单元 M k M_k Mk 与 M v M_v Mv 作为key与value来增强网络能力。外部注意力的计算最终变成了:
A = Norm ( F M k T ) F out = A M v A = \text{Norm}(FM_k^T ) \\ F_{\text{out}}=AM_v A=Norm(FMkT)Fout=AMv
此时的计算复杂度为 O ( d S N ) O(dSN) O(dSN) ,其中d与S为超参数,实际发现S取值为64就可以得到不错的效果。该方法计算量与像素数量呈现线性关系,相比自注意力机制在输入尺寸较大时效率更高。
自注意力机制使用了softmax来保证注意力图满足 ∑ j α i , j = 1 \sum_j\alpha_{i,j} = 1 ∑jαi,j=1 。注意力图是通过矩阵相乘来计算的,对于输入特征的尺度敏感。为解决这一问题,作者使用了双重归一化分别归一化行与列。
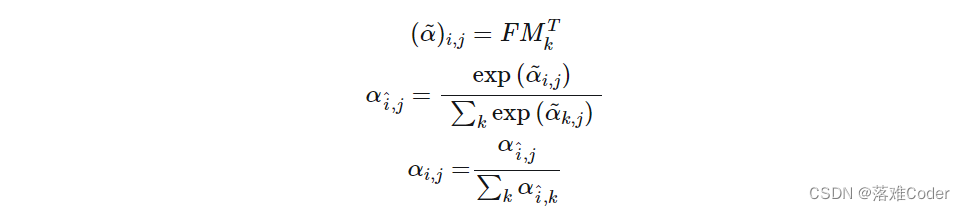
以上就是外部注意力的核心内容。为了证明外部注意力的有效性,作者在原文中开展了一系列实验包括:图像分类、语义分割、图像生成、点云分类与点云分割。限于篇幅这里不再列出。
相比自注意力机制,外部注意力中的Key与Value被拿到了外部,不再由特征投射产生。这种结构使得外部的记忆单元可以习得整个数据集样本的统计特征。使用两个线性单元作为外部注意力的记忆单元则简化了运算复杂度。