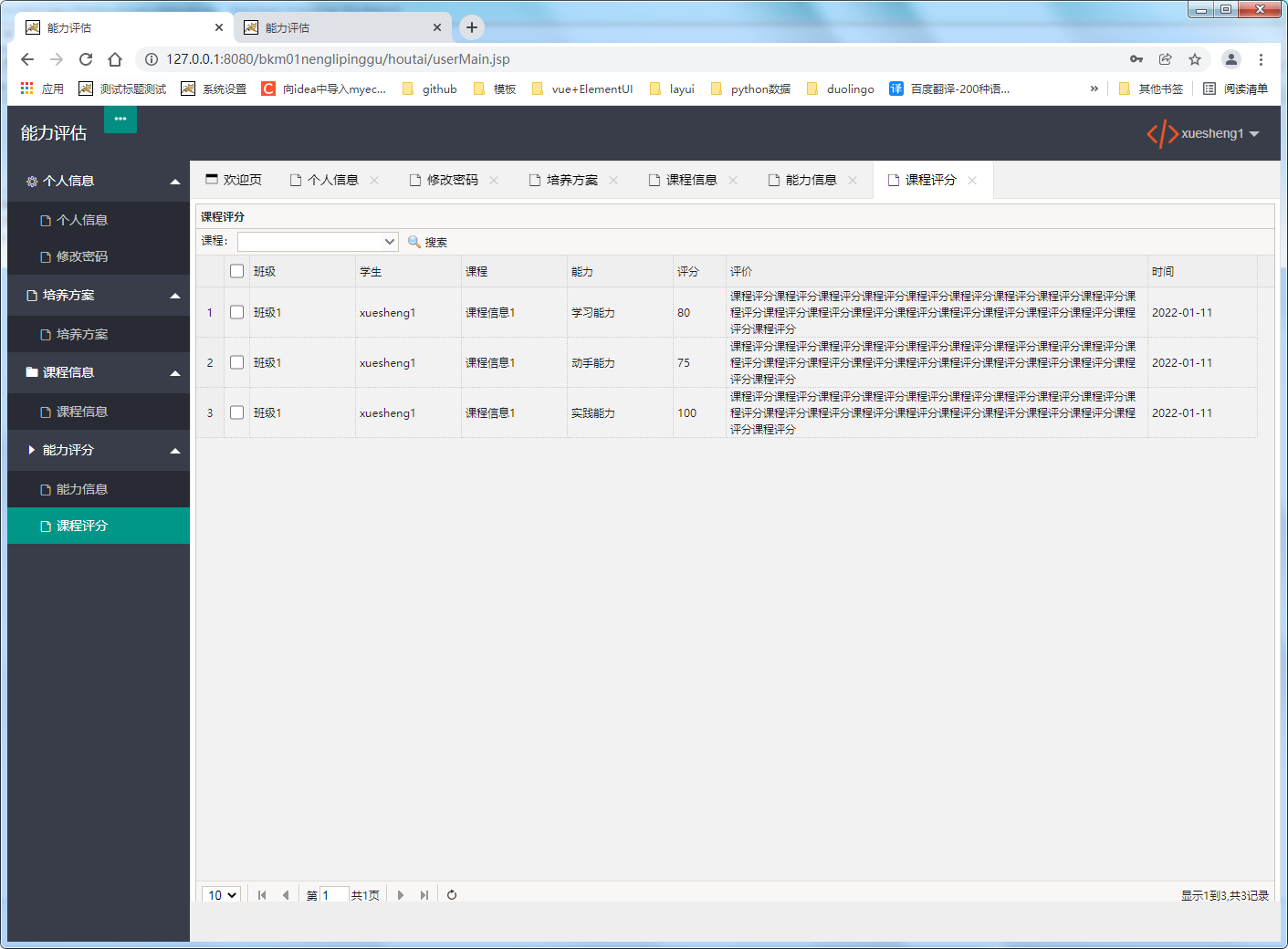
文章目录
- 前言
- 快速排序
- 关键点
- 实现
- 选角
- 排序
- 重复
- 实现
- 稳定性分析
- 记忆模板
- 归并排序
- 关键点
- 实现
- 二分查找
- 总结
前言
先来一波预热,本次寒假将要更新的博文系列为:基础算法部分,最新前言论文研读(不包含论文复现-耗时太长),C++基础博文系列,WhiteHole开发日志系列。那么在基础算法系列的话,我们这边采用的演示及其开发语言暂时选定为python,后续我们再考虑引入C++,也就是双版本。
快速排序
首先我们来看到最简单比较好理解的快速排序算法。这里我们假设都是从小打到排。
首先我们来理解一下这个快速排序的思路。快速排序要做到的其实非常简单,它的核心思想解释起来就一个句话:认清楚自己的位置
什么意思,就是让每一个数字都认识到自己应该放在哪里。找清楚自己的位置在哪里,所以整个算法的核心就在于这里,如何能够让一个数字找到自己的位置,摆正自己的方向。
我们拿最朴素的例子来讲解,那就是身高排序嘛,我们随便先拉出一个同学A,然后我们只需要保证,比这个同学A个子矮的排在左边,高的排在右边。之后我们在从比较矮小的个子的同学里面再挑选一个,然后再去对比,由于刚刚那个同学A往右都是高个子,左边的不可能比A右边的高,因此我们只需要比较到A就好了,同理,我们从A开始再从右边开始选一个同学,然后比较,(这里我们需要注意的就是不能再选到A同学去和右边的同学比较因为右边的都是比A高的)这样一来,我们重复几次操作,不就把整个队列都排好序号了吗。所以我们的快排其实就是仿造这个例子,来进行实现的。
关键点
所以通过刚刚的例子我们不难发现,快速排序其实就是大概三个关键步骤。
- 找一个标杆,需要参与对比的同学A(选角)
- 做一个排序,把比A小的放在左边,比A大的放在右边(排序)
- 重复操作,把A左边的和右边的按照1,2步骤进行重复操作,直到整个序列排完了。(重复)
整个过程就像,卷心菜一样,一层一层往里面拨开,先拨开最外面的,然后拨开到最里面。
实现
选角
那么接下来我们就进行简单实现一下喽。首先是我们要找到一个标杆,那么此时我们假设有这样的一个序列:
a = [2,5,4,3,8,4,2,1]
那么这个时候呢,有好多种做法,要么就是找中间的,要么就是找最左边的,或者随机找一个,这些都可以,至于哪一个更快这个得看情况,不好说。那么这边咱们也是来个最简单的那就是直接拿最左边的就好了。
排序
之后就是如何排序了,那么毫无疑问我们这边有非常多的方案,我们可以直接暴力排序,也就是直接遍历,我们再拿一个数组,然后开始比较,比选出来的数字A小的我们就直接放到新的数组里面的第一个位置,依次序放置,然后遇到大的我们就先放到最后面那个位置,然后往前依次序放置。
当然这样做有失风范,因此的话我们有更加优雅一点点的方案。还是基于刚刚的思路,我们搞一个双指针,分别放置在左右两侧

也就是i,j,然后呢我们还是一样的,左边的找到比A大的,右边的找到比A小的,然后我们在交换他们的位置,之后两个指针继续往中间移动,当指针重合的时候,那么这个A就找到了位置,此时已经是左小,右大了。
重复
之后就是重复了,那么这个不就更好办了嘛,我们直接把A左边的看着新的序列,右边的也看成新的序列呗。这个不就是所谓的分治思想嘛。
OK,现在我们问题都解决了,是时候亮出代码了
实现
def quick_sort(a:list,l:int,r:int):
if(l>=r):
return
# 选择一个需要被比较的玩意
division_key=a[l]
# 设置两个指针,初始化先指向左右两侧
# 这样做的目的是为了方便下标索引
i,j=l-1,r+1
while(i<j):
j-=1
i+=1
while(a[j]>division_key):
j -= 1
while(a[i]<division_key):
i += 1
if(i<j):
a[i] = a[i]+a[j]
a[j] = a[i]-a[j]
a[i] = a[i]-a[j]
quick_sort(a,l,j)
quick_sort(a,j+1,r)
def main():
a = [2,5,4,3,8,4,2,1]
print("排序前",a)
quick_sort(a,0,len(a)-1)
print("排序后",a)
if __name__ == '__main__':
main()
在这里我们做了一点点的处理,首先就是,为了方便下标索引同时为了避免出错,我们这边现将两个指针移到边界外面。
第二个就是,由于是数值交换,所以的话我们这边可以选择直接
a[i] = a[i]+a[j]
a[j] = a[i]-a[j]
a[i] = a[i]-a[j]
完成位置交换
稳定性分析
之后我们来到稳定性分析,首先我们都知道这个玩意是不稳定的,为什么不稳定,因为元素的相对位置会发生改变。
我们来把我们刚刚的例子做一个改动:
def quick_sort(a:list,l:int,r:int):
if(l>=r):
return
# 选择一个需要被比较的玩意
division_key=a[l][0]
# 设置两个指针,初始化先指向左右两侧
# 这样做的目的是为了方便下标索引
i,j=l-1,r+1
while(i<j):
j-=1
i+=1
while(a[j][0]>division_key):
j -= 1
while(a[i][0]<division_key):
i += 1
if(i<j):
temp = a[j]
a[j] = a[i]
a[i] = temp
quick_sort(a,l,j)
quick_sort(a,j+1,r)
def main():
a = [[2,1],[5,2],[4,3],[3,4],[8,5],[4,6],[2,7],[1,8]]
print("排序前",a)
quick_sort(a,0,len(a)-1)
print("排序后",a)
if __name__ == '__main__':
main()
之后我们来看到结果:

我们把刚刚的数据格式换一下,我们可以发现相同数字2的相对次序发生了改变。如果我们把这个次序当做是一个先后顺序,并且期望按照次序实现越早到达的越先进行显然就不合理了。那么为什么会出现这种情况你呢,因为每次我们都是直接进行交换的,根本不会去考虑次序,这个时候有小伙伴可能会问了,如果我判断一下,就是说,相等我们不交换行不行。
我们把交换的代码这样改一下:
if(i<j):
if(a[j][0]!=division_key):
temp = a[j]
a[j] = a[i]
a[i] = temp
然后我们多加一点干扰
a = [[2,1],[5,2],[4,3],[3,4],[8,5],[4,6],[2,7],[1,8],[2,9],[4,10],[8,11]]
理论上来说,i,j所指向的位置,要么是>=A ,要不及时<=A,当j指向的值!=A的时候那就是一定小于A,那么必然要到左边,i此时也将可以保证右边一定是>=A,因为此时i所指向的就是>=A的重复操作后一定可以保证这个结果。
结果上看

但是事实一定如此嘛?
我们不妨直接用代码伪造数据:
def getList():
size = 1000
rand = random.randint
res = []
for i in range(1,size+1):
temp = [rand(0,1e5),i]
res.append(temp)
return res
def isAsc(a):
i,j=0,1
for i in range(len(a)-2):
if(a[i][0]>a[j][0]):
return False
if(a[i][0]==a[j][0] and a[i][1]>a[j][1]):
return False
i+=1;j+=1
return True
之后我们再来看看效果
def main():
a = getList()
print("排序前",a)
quick_sort(a,0,len(a)-1)
print(isAsc(a))
print("排序后",a)
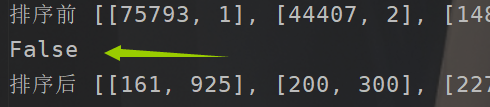
可以看到,结果并非我们所想,为什么呢,其实我们刚刚只是保证了A在排序A的时候一定不会乱序,但是在排序比较的过程中,别人的身高或者大小是一样的时候我们还是直接交换了,这样一来次序有可能就会被打乱。例如左边两个相同的值挨着那就直接会进行交换,这样一来相同的值自然就乱序了,这个时候你可能又会说了,拿相同我也不交换呗,我再拿几个指针去判断呗,那问题来了,我们一次性可以做到同时排序多个值?我们最终只能确定一个A在当前的序列里面的相对位置吧,当序列划分之后,排序后的相对位置可能还是有序的,但是在整体就就不一定了呀。
因此快速排序,很难是可以变成稳定的,难点就在于,你必须处理中间比较的时候,那些相同的值也需要保证有序。那么如何保证,其实也简单,前面就已经给了答案,给点提示就是一开始我们已经给出了一个比较暴力的排序方案。
记忆模板
OK,我们现在可以提取出我们快排的一个模板了,就是这个:
def quick_sort(a:list,l:int,r:int):
if(l>=r):
return
# 选择一个需要被比较的玩意
division_key=a[l]
# 设置两个指针,初始化先指向左右两侧
# 这样做的目的是为了方便下标索引
i,j=l-1,r+1
while(i<j):
j-=1
i+=1
while(a[j]>division_key):
j -= 1
while(a[i]<division_key):
i += 1
if(i<j):
temp = a[j]
a[j] = a[i]
a[i] = temp
quick_sort(a,l,j)
quick_sort(a,j+1,r)
是的和一开始的代码几乎一样。
- 终止条件 l>=r
- 选择一个数
- 找出两边小于和大于的位置,然后交换元素
- 通过j去划分左右两边的序列
为什么按照j去划分,因为有可能i往右边偏向的更多,二者相差不一定是1,所以在这个模板里面按照j去,j是右边那个指针
归并排序
OK,说完了快速我们再来说一下归并排序,这个排序的话和我们先前提到的快速排序是有一点点的不同,先前我们按照数来极限划分,现在的话我们按照这个区域来划分。
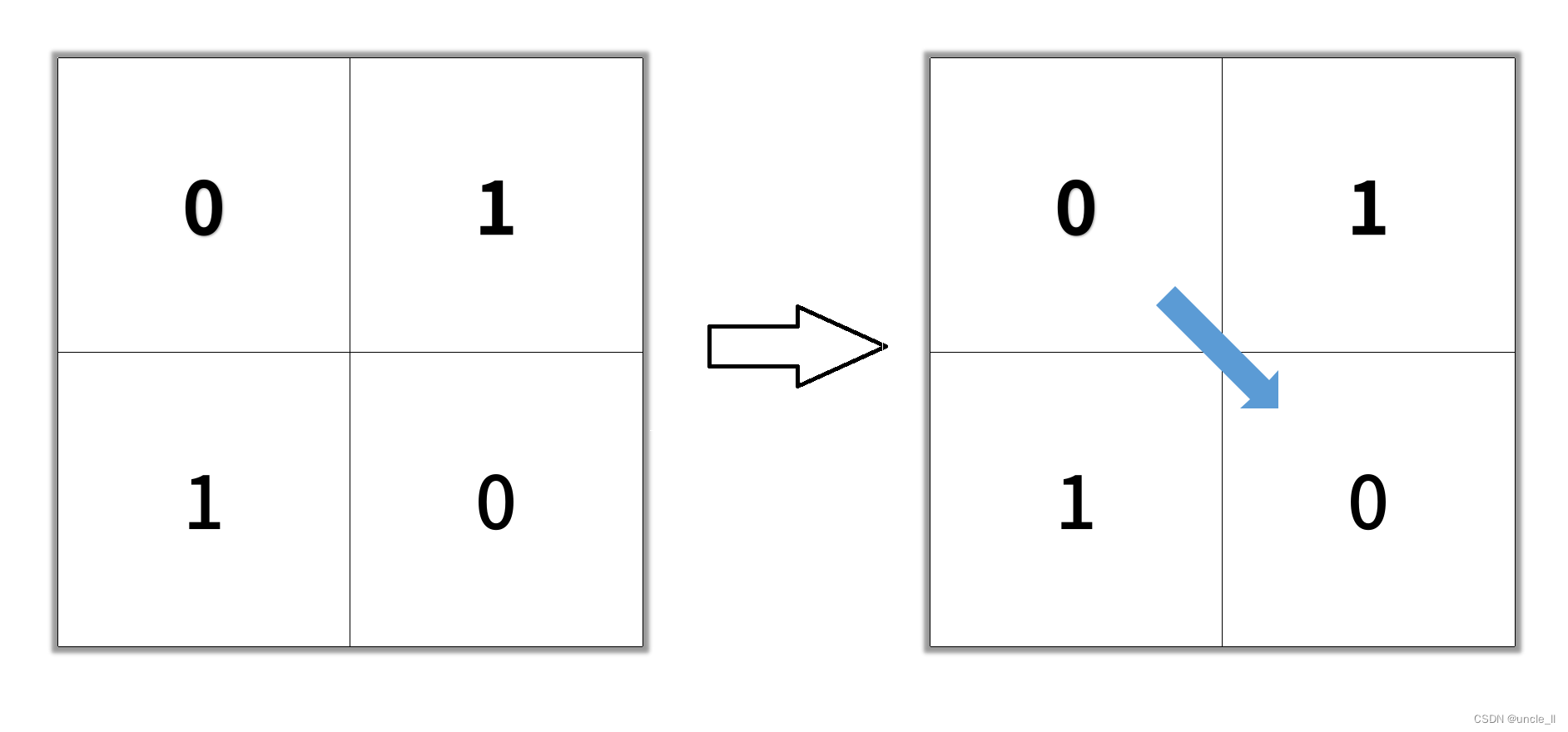
什么意思,一句话总结:局部有序到全局有序。这个的话不太好理解,我们就先来分析一下这个归并排序的时间复杂度吧。
首先归并排序呢,会先把一个序列进行划分,分割,对半划分,也就是最后的话,我们会把一个序列一直划分为长度为1,那么在每一层进行一个排序,由底层向上,最终完成一个排序,大概图例如下:

那么如果理解了这个,那么后面就好办了。
我们要做其实就是不断划分,划分,划分完毕之后的话,我们在进行一个排序,为了使得算法稳定,因此我们这边选择稍微暴力一点的方案,那就是直接两两对比,之后按次序放到零时数组里面。
当我们判断到只有一个数字的时候,跳出递归,此时对周围两个数字进行排序,完毕之后,再次跳出当前递归,对四个进行排序,(当然值得一提的是,每一层其实在计算的时候也是一棵树)
关键点
- 先划分
- 做排序,我们对两边进行归并
- 复制转移排序后的数字
实现
OK,这块我们直接看到代码:
def merge_sort(a:list,temp:list,l:int,r:int):
# 这个时候是说明已经划分到只有一个了
if(l>=r): return
mid = int((l+r)/2)
merge_sort(a,temp,l,mid)
merge_sort(a,temp,mid+1,r)
#这个时候我们需要进行一个归并
k=0
i,j=l,mid+1
while(i<=mid and j<=r):
if(a[i]<a[j]):
temp[k]=a[i]
i+=1
else:
temp[k]=a[j]
j+=1
k+=1
#判断左半边和右半边那一边没有循环完毕
while(i<=mid):
temp[k]=a[i]
k+=1
i+=1
while(j<=r):
temp[k] = a[j]
k += 1
j += 1
#对结果重新赋值
i = l
k = 0
while(i<=r):
a[i]=temp[k]
k+=1
i+=1
def main():
a = [2,5,4,3,8,4,2,1]
temp = [0 for _ in range(len(a))]
print("排序前",a)
merge_sort(a,temp,0,len(a)-1)
print("排序后",a)
if __name__ == '__main__':
main()
至于模板,就是上面这个。用其他的语言支持++操作的可能会更简洁一点。
二分查找
这个算法,我想应该就不太需要在本文中进行仔细阐述了吧。我们还是可以直接看到算法:
现在我们给定一个有序的序列,然后找到值为A的数字在数组中是第几个。
def binary_search(a,l,r,target):
if(l>r):
return -1
mid = l+int((r-l)/2)
if(target==a[mid]):
return mid
if(target<a[mid]):
#更小可能在左边
return binary_search(a,l,mid-1,target)
else:
return binary_search(a,mid+1,r,target)
def main():
a = [10, 14, 19, 26, 27, 31, 33, 35, 42, 44]
print("目标为第:",binary_search(a,0,len(a)-1,10)+1,"个数字")
if __name__ == '__main__':
main()
核心就是,二分递归查找嘛,那么有什么注意点呢,第一序列一定是有序,或者满足一个条件的。也会是说如果写出模板的话就应该是这样的:
def binary_search(a,l,r,target):
if(l>r):
return -1
mid = l+int((r-l)/2)
if(accept()):
return mid
if(check()):
#更小可能在左边
return binary_search(a,l,mid-1,target)
else:
return binary_search(a,mid+1,r,target)
注意点就是注意边界的问题。然后是我们中间点mid的取值的方式的问题,这个需要结合实际。
总结
今天的话就先水到这里,先缓缓恢复一下状态。





![[附源码]Python计算机毕业设计非处方药的查询与推荐系统Django(程序+LW)](https://img-blog.csdnimg.cn/71fdb38623bb481f821877e52ddbb4b0.png)
![[ vulhub漏洞复现篇 ] struts2远程代码执行漏洞s2-059(CVE-2019-0230)](https://img-blog.csdnimg.cn/b6672e2d9bd34a539d4364b2db053d15.png)


![[附源码]Nodejs计算机毕业设计基于Web的在线音乐网站Express(程序+LW)](https://img-blog.csdnimg.cn/5b0960558e204976acdfd9359a8e564b.png)