121. 买卖股票的最佳时机
1. 确定dp数组(dp table)以及下标的含义
用二维dp数组表示第i天的2种状态
dp[i][0] 表示第i天持有股票所得最多现金,可能i-1天就买股票了
dp[i][1] 表示第i天不持有股票所得最多现金
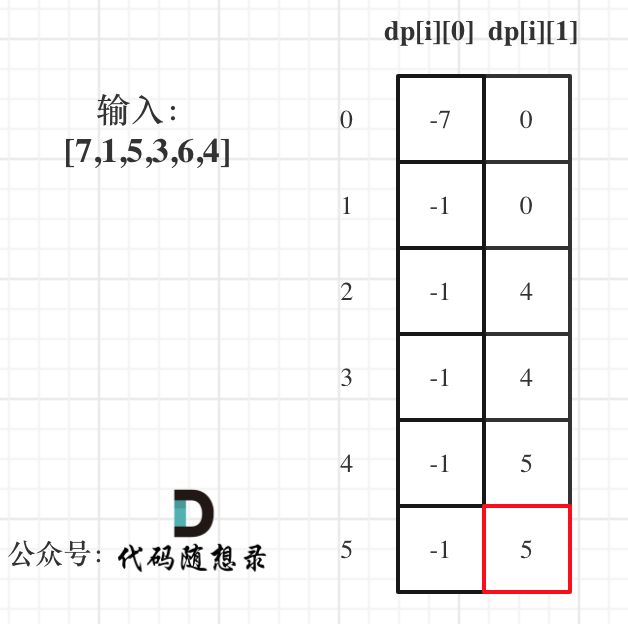
最后求:dp[len-1][0] dp[len-1][1]
2. 确定递推公式
dp[i][0]由哪些状态推出?
dp[i][0] = dp[i-1][0] 前一天是持有股票最大现金,一直延续持有股票的状态。
-price[i]在第i天买入股票,就变成持有股票的状态。(本题买卖就一次,买肯定是第一次买,直接就是负的)
dp[i][0] = max(dp[i-1][0], -price[i]); 求最大值
--------------------------------------------------------------------------------------------------------------------------------
dp[i][1] = dp[i-1][1] 前一天也可以是不持有股票最大现金,一直延续不持有股票的状态。
dp[i-1][0]+price[i] 前一天持有股票, 在第i天把股票卖了,就变成不持有股票的状态。加上股票价格price[i]。
dp[i][1] = max(dp[i-1][1], dp[i-1][0]+price[i]); 求最大值
3. dp数组如何初始化
递推公式基础:第0天持有 / 不持有股票
dp[0][0] = -prices[0]; // 持有股票的最大现金,买入股票,现金变负数,初始现金为0
dp[0][1] = 0;
4. 确定遍历顺序
从前往后遍历
0的状态已经初始化,i从1开始
for (int i = 1; i < len; i++) {
dp[i][0] = max(dp[i - 1][0], -prices[i]);
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
}持有股票一定没有不持有股票现金多,输出dp[len-1][i]即可,不用求max(dp[len-1][0], dp[len-1][1])
5. 举例推导dp数组
class Solution {
public:
int maxProfit(vector<int>& prices) {
int len = prices.size();
if (len==0) return 0;
vector<vector<int>> dp(len, vector<int>(2)); //len*2的二维vector
dp[0][0] -= prices[0];
dp[0][1] = 0;
for (int i=1; i<len; i++){
// 前一天是持有股票最大现金,一直延续持有股票的状态
// 在第i天买入股票,变成持有股票的状态
dp[i][0]=max(dp[i-1][0], -prices[i]);
// 前一天可以是不持有股票最大现金,一直延续不持有股票的状态
// 前一天持有股票, 在第i天把股票卖了,就变成不持有股票的状态。
dp[i][1]=max(dp[i-1][1], dp[i-1][0]+prices[i]);
}
return dp[len-1][1];
}
};122.买卖股票的最佳时机II
股票可以买卖多次。-> 卖出一样,买入不一样了。
持有股票最大现金的状态和上一题不同。
手头现金非0,可能是之前买卖多次获得的利润。
不是0-price[i],是前一天不持有股票的最大现金dp[i-1]减去当天的价格:dp[i - 1][1] - prices[i]
在第i天买入股票,就变成持有股票的状态。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int len = prices.size();
vector<vector<int>> dp(len, vector<int>(2, 0));
dp[0][0] -= prices[0];
dp[0][1] = 0;
for (int i = 1; i < len; i++) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); // 注意这里是和121. 买卖股票的最佳时机唯一不同的地方。
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
}
return dp[len - 1][1];
}
};