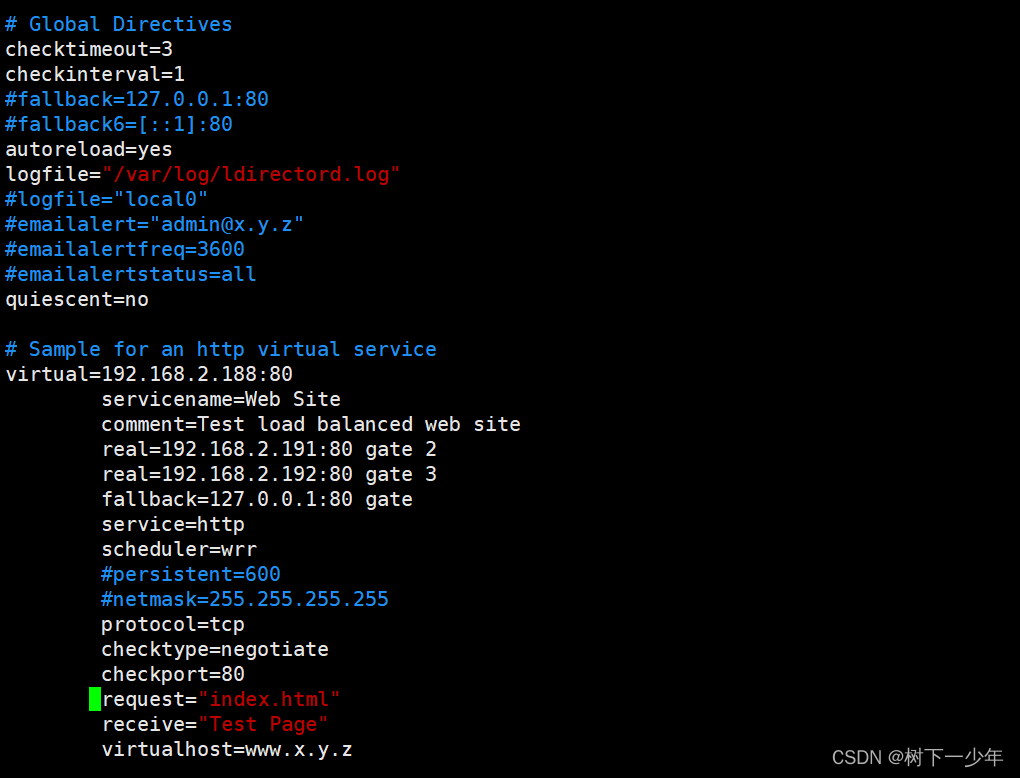
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：

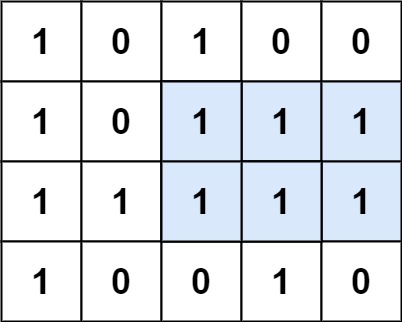
 思路一：单调栈

int maximalRectangle(char** matrix, int matrixSize, int* matrixColSize){
    int dp[matrixSize][matrixColSize[0] + 2];
    memset(dp, 0, sizeof(dp));//初始化
    for(int i = 0; i < matrixSize; i++)
    {
        for(int j = 0; j < matrixColSize[0]; j++)
        {
            if(matrix[i][j] == '1')
            {
                dp[i][j+1] = (i == 0 ? 0 : dp[i-1][j+1])+1;
            }
        }
    }
    int max = 0;
    for(int i = 0; i < matrixSize; i++)
    {
        int stack[matrixColSize[0]+2];
        int top = -1;
        stack[++top] = 0;
        for(int j = 1; j < matrixColSize[0]+2; j++)
        {
                while(dp[i][j] < dp[i][stack[top]])
                {
                    max = fmax(max, (j - stack[top-1] - 1) * dp[i][stack[top]]);
                    --top;
                }
                stack[++top] = j;
        }
    }
    return max;
}

 分析：

本题与上题相似，同为单调栈解法，可将矩形转换为长和宽，计算长宽的乘积最大值，根据单调递减递归到最小值计算矩形最大值，最后返回答案

总结：

本题考察单调栈的应用，除此之外本题还可用动态规划的方法解决，单调栈解法注意对数组处理，输入的为字符串，与数字处理方法有差异