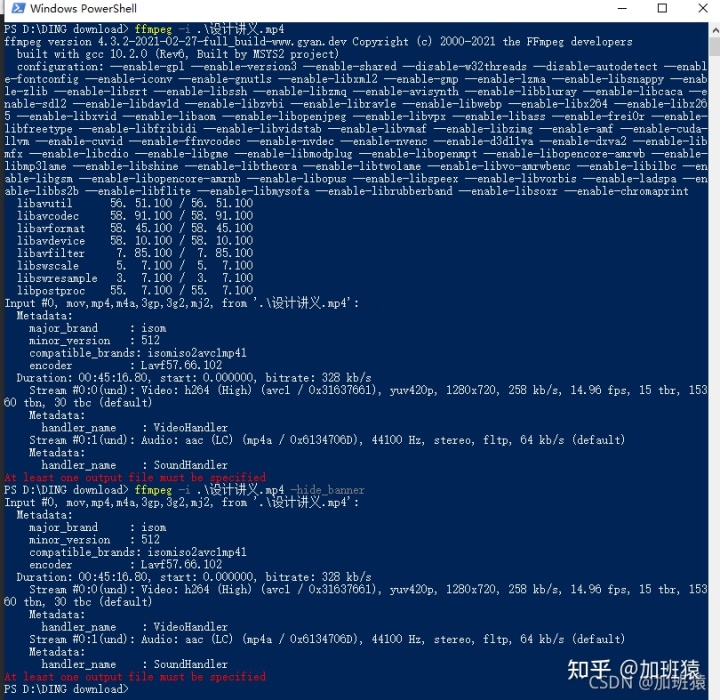
123.买卖股票的最佳时机III

此题限定了买卖的次数，所以应该用几个状态来记录所对应得利润
至多买卖两次，这意味着可以买卖一次，可以买卖两次，也可以不买卖。

dp数组及下标含义

一天一共就有五个状态，
0 没有操作
1 第一次买入
2 第一次卖出
3 第二次买入
4 第二次卖出
dp[i][j]中 i表示第i天，j为 [0 - 4] 五个状态，dp[i][j]表示第i天状态j所剩最大现金。
确定递推公式
需要注意：dp[i][1]，表示的是第i天，买入股票的状态，并不是说一定要第i天买入股票，这是容易陷入的误区。
- 达到dp[i][1]状态，有两个具体操作：
  - 操作一：第i天买入股票了，那么dp[i][1] = dp[i-1][0] - prices[i]
  - 操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][1] = dp[i - 1][1]
  所以dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][1]);
- 同理dp[i][2]也有两个操作：
  - 操作一：第i天卖出股票了，那么dp[i][2] = dp[i - 1][1] + prices[i]
  - 操作二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i][2] = dp[i - 1][2]
  所以dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])
- 同理可推出剩下状态部分：
  
  dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
  
  dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
dp数组初始化
第0天没有操作，就是0，即：dp[0][0] = 0;

第0天做第一次买入的操作，dp[0][1] = -prices[0];

第0天做第一次卖出的操作，所以dp[0][2] = 0;

第0天第二次买入操作，第二次买入依赖于第一次卖出的状态，此时相当于第0天第一次买入了，第一次卖出了，然后在买入一次（第二次买入），那么现在手头上没有现金，只要买入，现金就做相应的减少。

所以第二次买入操作，初始化为：dp[0][3] = -prices[0];

同理第二次卖出初始化dp[0][4] = 0;
确定遍历顺序
从递归公式其实可以看出，从前向后遍历，因为dp[i]，依靠dp[i - 1]的数值。
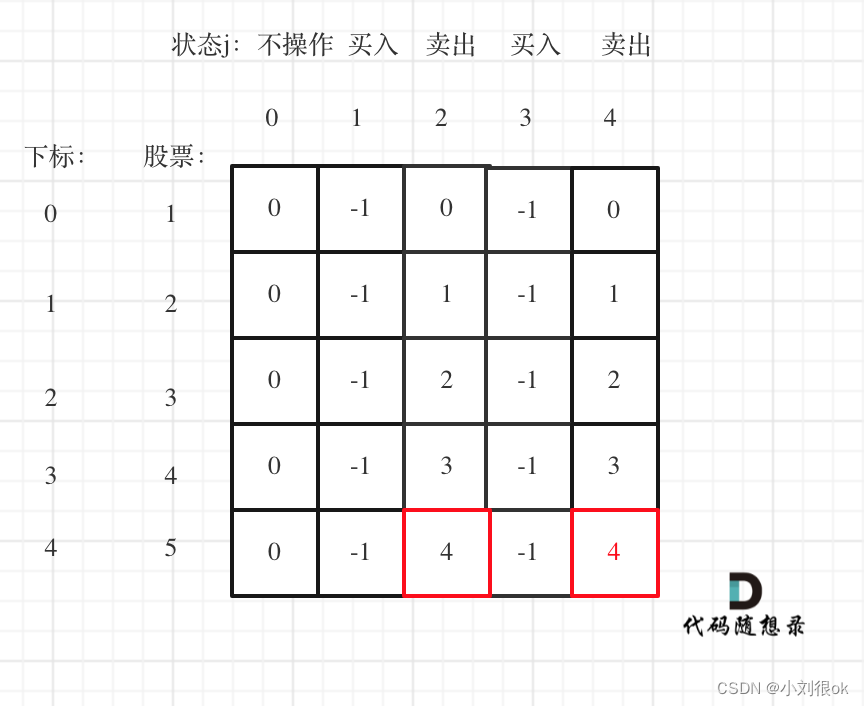
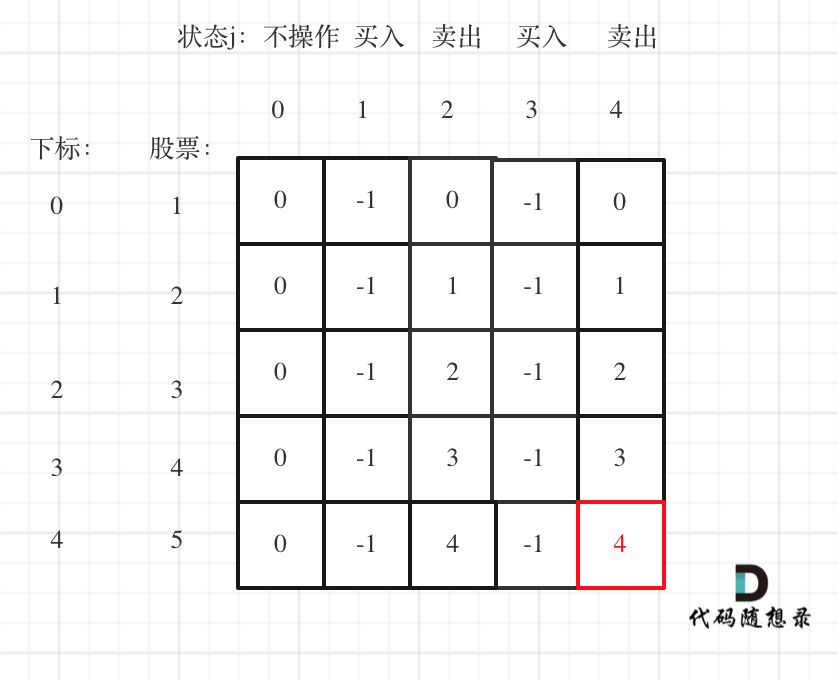
举例推导dp数组
以输入[1,2,3,4,5]为例

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        vector<vector<int>> dp(prices.size(), vector<int>(5));
        //dp[0][0] = 0;
        dp[0][1] = -prices[0];
        //dp[0][2] = 0;
        dp[0][3] = -prices[0];
        //dp[0][4] = 0;
        for (int i = 1; i < prices.size(); i++) {
            dp[i][0] = dp[i - 1][0];
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
        }
        return dp[prices.size() - 1][4];
    }
};

188.买卖股票的最佳时机IV

此题为上一题的升级版，将买卖最大次数一般化为k次

首先不同的地方在于初始化，通过上题规律可以看出，当状态j为奇数时为买入，为偶数时为卖出
所以初始化为

        for (int i = 1; i <= 2 * k; i += 2) {
            dp[0][i] = -prices[0];
        }

下一个不同的地方就在于递推公式，同样也是区分奇偶数

        for (int j = 0; j < 2 * k - 1; j += 2) {
            dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]); //对应奇数
            dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]); //对应偶数
        }

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        if (prices.size() == 0) return 0;
        vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1));
        for (int i = 1; i <= 2 * k; i += 2) {
            dp[0][i] = -prices[0];
        }
        for (int i = 1; i < prices.size(); i++) {
            //自己写的
            // for (int j = 1; j <= 2 * k; j++) {
            //     if (j % 2 == 1) {
            //         dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1] - prices[i]);
            //     } else if (j % 2 == 0) {
            //         dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1] + prices[i]);
            //     }
            // }
            
            //卡哥处理
            for (int j = 0; j < 2 * k - 1; j += 2) {
                dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]); //对应奇数
                dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]); //对应偶数
            }
        }
        return dp[prices.size() - 1][2 * k];
    }
};