探究主成分分析方法数学原理

news2024/9/28 7:25:36

目录

1、简介

2、实现原理

3、实现步骤

4、公式分析

5、实例分析

6、⭐协方差矩阵补充说明

7、LaTex文本

⭐创作不易，您的一键三连，就是支持我写作的最大动力！🥹

关于代码如何实现，请看这篇文章：[机器学习]特征工程：主成分分析_逐梦苍穹的博客-CSDN博客icon-default.png?t=N6B9https://blog.csdn.net/qq_60735796/article/details/132324240

1、简介

主成分分析（Principal Component Analysis，PCA）是一种常用的数据降维和特征提取技术，用于将高维数据转化为低维表示，同时保留数据的主要特征。

它通过线性变换将原始特征投影到新的坐标轴上，使得投影后的特征具有最大的方差，从而达到降低数据维度的目的。

PCA 的主要思想是寻找数据中的主要方向，即数据的主成分，这些主成分是数据变化最大的方向。通过保留最重要的主成分，可以将数据的维度减少，从而减少存储和计算的成本，同时可以降低数据中的噪声和冗余信息，提高模型的泛化能力。

2、实现原理

PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法。

PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。

PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。

其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。

依次类推，可以得到n个这样的坐标轴。

通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0。

于是，我们可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴。

事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

3、实现步骤

PCA 的工作步骤如下：

  1. 标准化数据
  2. 计算数据的协方差矩阵。
  3. 对协方差矩阵进行特征值分解，得到特征值和特征向量。
  4. 将特征值按从大到小的顺序排列，选择前几个特征值对应的特征向量作为主成分。
  5. 将原始数据投影到选定的主成分上，得到降维后的数据。

4、公式分析

①特征样本均值：\overline{x}= \frac{1}{n}\sum_{i=1}^{n}{x_i}

②特征样本方差：{S}^2= \frac{1}{n-1}\sum_{i=1}^{n}{(x_i-\overline{x})^2}

③特征方差：{S}^2= \frac{1}{n}\sum_{i=1}^{n}{(x_i-\overline{x})^2}

④协方差：\text{Cov}(X, Y) = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})

⑤协方差矩阵：\text{Cov}(X_1,X_2,...X_p) = \begin{bmatrix} \text{Cov}(X_1, X_1) & \text{Cov}(X_1, X_2) & \dots & \text{Cov}(X_1, X_p) \\ \text{Cov}(X_2, X_1) & \text{Cov}(X_2, X_2) & \dots & \text{Cov}(X_2, X_p) \\ \vdots & \vdots & \ddots & \vdots \\ \text{Cov}(X_p, X_1) & \text{Cov}(X_p, X_2) & \dots & \text{Cov}(X_p, X_p) \end{bmatrix}

⑥样本去中心化协方差：\boldsymbol{\Sigma} = \frac{1}{n} \mathbf{X}^T \mathbf{X}

⑦特征向量：Av=\lambda v

⑧特征值：令 |C-λE| =0

⑨特征向量标准化(先求特征向量的长度)：\mathbf{v}_{\text{std}} = \frac{\mathbf{v}}{||\mathbf{v}||}

5、实例分析

给出平面直角坐标系上的五个点：(-1,-2)，(-1, 0)，( 0, 0)，( 2, 1)，( 0, 1)，

所以矩阵为：x= \begin{pmatrix} -1 & -1 & 0 & 2 & 0 \\ -2 & 0 & 0 & 1 & 1 \end{pmatrix}

描点画图：

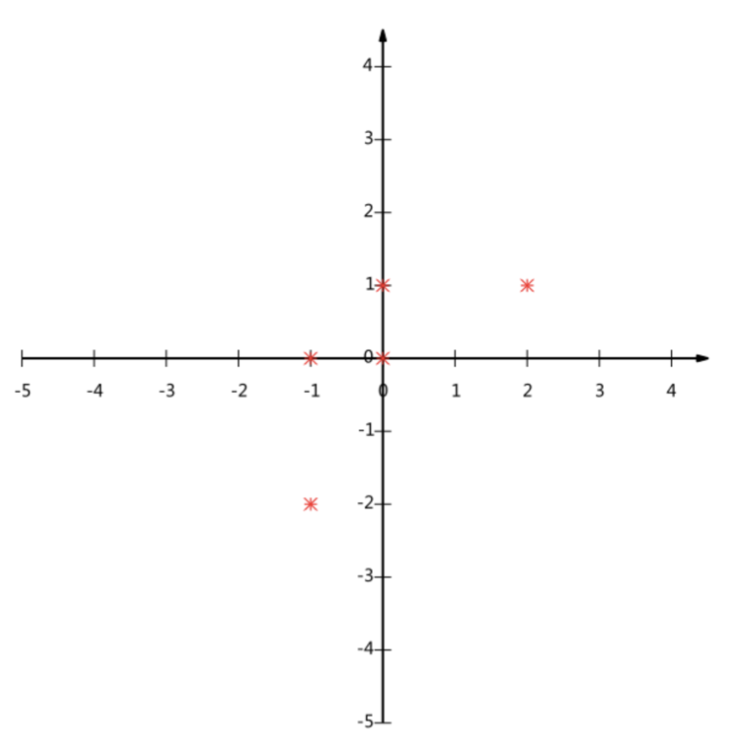
下面使用主成分分析方法进行降维，结果如下：

下面是主成分分析的实现过程：

①去中心化。由于这组数据的两个指标的平均值都为0，所以该样本就是去中心化样本。

所以该样本为：

X=x= \begin{pmatrix} -1 & -1 & 0 & 2 & 0 \\ -2 & 0 & 0 & 1 & 1 \end{pmatrix}

②计算标准差。这里的特征标准差都一致，所以这一步可以不用。

③计算协方差，这里因为数据去中心化了，所以使用的公式为：\boldsymbol{C} = \frac{1}{n} \mathbf{X}^T \mathbf{X} 

(后面细讲这个公式)

协方差计算过程为：

\boldsymbol{C} = \frac{1}{n} \mathbf{X} \mathbf{X}^T=\frac{1}{5}\begin{pmatrix} -1 & -1 & 0 & 2 & 0 \\ -2 & 0 & 0 & 1 & 1 \end{pmatrix} \begin{pmatrix} -1 & -2 \\ -1 & 0 \\ 0 & 0 \\ 2 & 1 \\ 0 & 1 \\ \end{pmatrix} =\begin{pmatrix} \frac{6}{5} & \frac{4}{5} \\ \frac{4}{5} & \frac{6}{5} \\ \end{pmatrix}

④特征值和特征向量：Cv=λv。

计算过程：

\begin{pmatrix} \frac{6}{5} & \frac{4}{5} \\ \frac{4}{5} & \frac{6}{5} \\ \end{pmatrix}\begin{pmatrix} v_1\\ v_2\\ \end{pmatrix}=\lambda\begin{pmatrix} v_1\\ v_2\\ \end{pmatrix}

整理一下，得出：

\begin{array}{l} \left\{\begin{matrix} \frac{6v_1}{5}+\frac{4v_2}{5}=\lambda v_1 \\ \frac{4v_1}{5}+\frac{6v_2}{5}=\lambda v_2 \end{matrix}\right. \end{array}

进行化简，得到：

\begin{array}{l} \left\{\begin{matrix} (\frac{6}{5}-\lambda )v_1+\frac{4v_2}{5}=0 \\ \frac{4v_1}{5}+(\frac{6}{5}-\lambda)v_2=0 \end{matrix}\right. \end{array}

行列式求解：

\begin{vmatrix} \frac{6}{5}-\lambda & \frac{4}{5}\\ \frac{4}{5}& \frac{6}{5}-\lambda \\ \end{vmatrix} =0

因式分解得：

\left(\lambda-\frac{2}{5}\right)\left(\lambda-2\right) =0

解得：λ1=2，λ2=2/5

特征值依次带入行列式的矩阵，乘以对应的特征向量，得：

\begin{pmatrix} \frac{6}{5}-\lambda & \frac{4}{5} \\ \frac{4}{5} & \frac{6}{5}-\lambda \\ \end{pmatrix}\begin{pmatrix} v_{i1}\\ v_{i2}\\ \end{pmatrix}=\begin{pmatrix} 0\\ 0\\ \end{pmatrix}

把λ1=2，λ2=2/5依次带入，得到：

\begin{pmatrix} \frac{6}{5}-2 & \frac{4}{5} \\ \frac{4}{5} & \frac{6}{5}-2 \\ \end{pmatrix}\begin{pmatrix} v_{11}\\ v_{12}\\ \end{pmatrix}= \begin{pmatrix} -\frac{4}{5} & \frac{4}{5} \\ \frac{4}{5} & -\frac{4}{5} \\ \end{pmatrix}\begin{pmatrix} v_{11}\\ v_{12}\\ \end{pmatrix}= \begin{pmatrix} 0\\ 0\\ \end{pmatrix}

最终特征向量v1为：C_1\begin{pmatrix} 1 \\ 1 \\ \end{pmatrix}

同理可得最终特征向量v2为：C_2\begin{pmatrix} -1 \\ 1 \\ \end{pmatrix}

其中对应的特征向量分别是一个通解，C1和C2可以取任意实数。那么标准化后的特征向量为：

v1：

\mathbf{v}_{\text{1}} = \frac{\mathbf{v_1}}{||\mathbf{v}||}= \frac{ \begin{pmatrix} 1 \\ 1 \end{pmatrix} }{ \sqrt{1^2+1^2} }=\frac{ \begin{pmatrix} 1 \\ 1 \end{pmatrix} }{ \sqrt{2} }=\begin{pmatrix} \frac{1}{\sqrt{2} } \\ \frac{1}{\sqrt{2} } \end{pmatrix}

v2：

\mathbf{v}_{\text{2}} = \frac{\mathbf{v_1}}{||\mathbf{v}||}= \frac{ \begin{pmatrix} -1 \\ 1 \end{pmatrix} }{ \sqrt{(-1)^2+1^2} }=\frac{ \begin{pmatrix} -1 \\ 1 \end{pmatrix} }{ \sqrt{2} }=\begin{pmatrix} -\frac{1}{\sqrt{2} } \\ \frac{1}{\sqrt{2} } \end{pmatrix}

所以特征矩阵为：

P=\begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix}

⑤选取主成分：

取p1和p2：

p_1=\begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix}

p_2=\begin{pmatrix} -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix}

最后结果公式为：Y=PX，带入p1，得Y=p1X：

Y=p_1X=\begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} -1 & -1 & 0 & 2 & 0 \\ -2 & 0 & 0 & 1 & 1 \end{pmatrix} =\begin{pmatrix} -\frac{3}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 & \frac{3}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix}

带入p2同理，但是最终主成分分析的结果，应取带入p1为佳，投影到一维坐标之后，矩阵元素点到新坐标原点的距离之和，， 带入p1大于p2。

6、⭐协方差矩阵补充说明

样本去中心化协方差：\boldsymbol{C} = \frac{1}{n} \mathbf{X} \mathbf{X}^T

我们来推导一下协方差矩阵公式\boldsymbol{C} = \frac{1}{n} \mathbf{X} \mathbf{X}^T的原理：

假设我们有一个数据矩阵 X，其中每一行表示一个观测样本，每一列表示一个特征。假设数据已经被中心化，即每个特征的均值为零。

协方差矩阵的元素 Cov(Xi,Xj) 表示随机变量 Xi 和 Xj 之间的协方差。协方差的计算公式为：

\text{Cov}(X, Y) = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})

其中，xki 表示第 k 个样本的第 i 个特征值，xˉi 表示第 i 个特征的均值，n 表示观测样本数。

我们可以把数据矩阵 X 写成如下形式：

X=\begin{pmatrix} a_{11} & a_{12} &\cdots & a_{1p} \\ a_{21} & a_{22} & \cdots & a_{2p} \\ \vdots & \ddots & \vdots & \vdots\\ a_{n1} & a_{n2}&\cdots & a_{np} \end{pmatrix}

其中，每一行对应一个观测样本，每一列对应一个特征。

我们现在考虑协方差矩阵的一个元素Cov(Xi,Xj)：

\text{Cov}(X_i, Y_i) = \frac{1}{n} \sum_{k=1}^{n} (x_{ki} - \bar{x_i})(x_{ki} - \bar{x_j})

我们可以把这个元素的计算写成矩阵形式，将每一列表示一个特征向量，得到如下形式：

\text{Cov}(X_i, Y_i) = \frac{1}{n} (X_{i} - \bar{x_i})^T(X_{j} - \bar{x_j})

其中，Xi 是第 i 个特征的列向量，xˉi 是第 i 个特征的均值列向量。

现在我们可以考虑协方差矩阵的计算，可以表示为矩阵乘积的形式：

\boldsymbol{\Sigma}= \frac{1}{n} (X_{} - \bar{x})^T(X_{} - \bar{x})

其中，X 是数据矩阵，xˉ 是均值矩阵，每一列表示对应特征的均值。

将 X 展开成列向量形式，我们可以得到：

\boldsymbol{\Sigma}= \frac{1}{n} X^TX

这就得到了协方差矩阵的计算公式。需要注意的是，这个公式是在数据已经中心化的基础上进行推导的。

在实际应用中，如果数据没有被中心化，还需要额外的操作来考虑均值的影响。

7、LaTex文本

文中所有公式对应的LaTex表达式都放这里了：

4、公式分析
①特征样本均值：\overline{x}= \frac{1}{n}\sum_{i=1}^{n}{x_i}
②特征样本方差：{S}^2= \frac{1}{n-1}\sum_{i=1}^{n}{(x_i-\overline{x})^2}
③特征方差：{S}^2= \frac{1}{n}\sum_{i=1}^{n}{(x_i-\overline{x})^2}
④协方差：\text{Cov}(X, Y) = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})
⑤协方差矩阵：\text{Cov}(X_1,X_2,...X_p) = \begin{bmatrix}
\text{Cov}(X_1, X_1) & \text{Cov}(X_1, X_2) & \dots & \text{Cov}(X_1, X_p) \\
\text{Cov}(X_2, X_1) & \text{Cov}(X_2, X_2) & \dots & \text{Cov}(X_2, X_p) \\
\vdots & \vdots & \ddots & \vdots \\
\text{Cov}(X_p, X_1) & \text{Cov}(X_p, X_2) & \dots & \text{Cov}(X_p, X_p)
\end{bmatrix}
⑥样本去中心化协方差：\boldsymbol{\Sigma} = \frac{1}{n} \mathbf{X}^T \mathbf{X}
⑦特征向量：Av=\lambda v
⑧特征值：令 |C-λE| =0
⑨特征向量标准化(先求特征向量的长度)：\mathbf{v}_{\text{std}} = \frac{\mathbf{v}}{||\mathbf{v}||}

给出平面直角坐标系上的五个点：(-1,-2)，(-1, 0)，( 0, 0)，( 2, 1)，( 0, 1)，
所以矩阵为：x=
\begin{pmatrix}  
  -1 & -1 & 0 & 2 & 0 \\  
  -2 & 0 & 0 & 1 & 1  
\end{pmatrix} 

下面是主成分分析的实现过程：
①去中心化。由于这组数据的两个指标的平均值都为0，所以该样本就是去中心化样本。
所以该样本为：
X=x=
\begin{pmatrix}  
  -1 & -1 & 0 & 2 & 0 \\  
  -2 & 0 & 0 & 1 & 1  
\end{pmatrix} 
②计算标准差。这里的特征标准差都一致，所以这一步可以不用。
③计算协方差，这里因为数据去中心化了，所以使用的公式为：\boldsymbol{C} = \frac{1}{n} \mathbf{X}^T \mathbf{X} (后面细讲这个公式)
协方差计算过程为：
\boldsymbol{C} = \frac{1}{n} \mathbf{X} \mathbf{X}^T=\frac{1}{5}\begin{pmatrix}  
  -1 & -1 & 0 & 2 & 0 \\  
  -2 & 0 & 0 & 1 & 1  \end{pmatrix} \begin{pmatrix}  
  -1 & -2 \\  
  -1 & 0 \\ 
  0 & 0    \\ 
  2 & 1 \\ 
  0 & 1 \\ \end{pmatrix} =\begin{pmatrix}  \frac{6}{5} & \frac{4}{5} \\   \frac{4}{5} & \frac{6}{5} \\ \end{pmatrix}
④特征值和特征向量：Cv=λv。
计算过程：
\begin{pmatrix}  
  \frac{6}{5} & \frac{4}{5} \\  
  \frac{4}{5} & \frac{6}{5} \\ 
\end{pmatrix}\begin{pmatrix}  
   v_1\\  
  v_2\\ 
\end{pmatrix}=\lambda\begin{pmatrix}  
   v_1\\  
  v_2\\ 
\end{pmatrix}
整理一下，得出：
\begin{array}{l} 
  \left\{\begin{matrix} 
\frac{6v_1}{5}+\frac{4v_2}{5}=\lambda v_1 \\
\frac{4v_1}{5}+\frac{6v_2}{5}=\lambda v_2
\end{matrix}\right.    
\end{array} 
进行化简，得到：
\begin{array}{l} 
  \left\{\begin{matrix} 
(\frac{6}{5}-\lambda )v_1+\frac{4v_2}{5}=0 \\
\frac{4v_1}{5}+(\frac{6}{5}-\lambda)v_2=0
\end{matrix}\right.    
\end{array} 
行列式求解：
 \begin{vmatrix}  
  \frac{6}{5}-\lambda &  \frac{4}{5}\\  
  \frac{4}{5}& \frac{6}{5}-\lambda \\  
\end{vmatrix} =0
因式分解得：
\left(\lambda-\frac{2}{5}\right)\left(\lambda-2\right) =0
解得：λ1=2，λ2=2/5
特征值依次带入行列式的矩阵，乘以对应的特征向量，得：
\begin{pmatrix}  
  \frac{6}{5}-\lambda & \frac{4}{5} \\  
  \frac{4}{5} & \frac{6}{5}-\lambda \\ 
\end{pmatrix}\begin{pmatrix}  
   v_{i1}\\  
  v_{i2}\\ 
\end{pmatrix}=\begin{pmatrix}  
   0\\  
  0\\ 
\end{pmatrix}
把λ1=2，λ2=2/5依次带入，得到：
\begin{pmatrix}  
  \frac{6}{5}-2 & \frac{4}{5} \\  
  \frac{4}{5} & \frac{6}{5}-2 \\ 
\end{pmatrix}\begin{pmatrix}  
   v_{11}\\  
  v_{12}\\ 
\end{pmatrix}=
\begin{pmatrix}  
  -\frac{4}{5} & \frac{4}{5} \\  
  \frac{4}{5} & -\frac{4}{5} \\ 
\end{pmatrix}\begin{pmatrix}  
   v_{11}\\  
  v_{12}\\ 
\end{pmatrix}=
\begin{pmatrix}  
   0\\  
  0\\ 
\end{pmatrix}
最终特征向量v1为：C_1\begin{pmatrix}  
 1  \\  
 1 \\ 
\end{pmatrix}
同理可得最终特征向量v2为：C_2\begin{pmatrix}  
 -1  \\  
 1 \\ 
\end{pmatrix}
其中对应的特征向量分别是一个通解，C1和C2可以取任意实数。那么标准化后的特征向量为：
v1：
\mathbf{v}_{\text{1}} = \frac{\mathbf{v_1}}{||\mathbf{v}||}=
\frac{
\begin{pmatrix}  
  1 \\  
  1  
\end{pmatrix} 
}{
\sqrt{1^2+1^2} 
}=\frac{
\begin{pmatrix}  
  1 \\  
  1  
\end{pmatrix} 
}{
\sqrt{2} 
}=\begin{pmatrix}  
  \frac{1}{\sqrt{2} } \\  
  \frac{1}{\sqrt{2} }   
\end{pmatrix} 
v2：
\mathbf{v}_{\text{2}} = \frac{\mathbf{v_1}}{||\mathbf{v}||}=
\frac{
\begin{pmatrix}  
  -1 \\  
  1  
\end{pmatrix} 
}{
\sqrt{(-1)^2+1^2} 
}=\frac{
\begin{pmatrix}  
  -1 \\  
  1  
\end{pmatrix} 
}{
\sqrt{2} 
}=\begin{pmatrix}  
  -\frac{1}{\sqrt{2} } \\  
  \frac{1}{\sqrt{2} }   
\end{pmatrix} 
所以特征矩阵为：
P=\begin{pmatrix}  
  \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\  
  -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}  
\end{pmatrix} 
⑤选取主成分：
取p1和p2：
p_1=\begin{pmatrix}  
  \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}  
\end{pmatrix} 
p_2=\begin{pmatrix}  
  -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}  
\end{pmatrix} 
最后结果公式为：Y=PX，带入p1，得Y=p1X：
Y=p_1X=\begin{pmatrix}  
  \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}  
\end{pmatrix} \begin{pmatrix}  
  -1 & -1 & 0 & 2 & 0 \\  
  -2 & 0 & 0 & 1 & 1  
\end{pmatrix} =\begin{pmatrix}  
  -\frac{3}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 & \frac{3}{\sqrt{2}} & -\frac{1}{\sqrt{2}} 
\end{pmatrix} 
带入p2同理，但是最终主成分分析的结果，应取带入p1为佳，投影到一维坐标之后，矩阵元素点到新坐标原点的距离之和，， 带入p1大于p2。


6、⭐协方差矩阵补充说明
样本去中心化协方差：\boldsymbol{C} = \frac{1}{n} \mathbf{X} \mathbf{X}^T
我们来推导一下协方差矩阵公式\boldsymbol{C} = \frac{1}{n} \mathbf{X} \mathbf{X}^T的原理：
假设我们有一个数据矩阵 X，其中每一行表示一个观测样本，每一列表示一个特征。假设数据已经被中心化，即每个特征的均值为零。
协方差矩阵的元素 Cov(Xi,Xj) 表示随机变量 Xi 和 Xj 之间的协方差。协方差的计算公式为：
\text{Cov}(X, Y) = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})
其中，xki 表示第 k 个样本的第 i 个特征值，xˉi 表示第 i 个特征的均值，n 表示观测样本数。
我们可以把数据矩阵 X 写成如下形式：
X=\begin{pmatrix}  
  a_{11} & a_{12} &\cdots & a_{1p} \\  
  a_{21} & a_{22} & \cdots & a_{2p} \\
  \vdots & \ddots & \vdots & \vdots\\  
  a_{n1} & a_{n2}&\cdots & a_{np}  
\end{pmatrix} 
其中，每一行对应一个观测样本，每一列对应一个特征。
我们现在考虑协方差矩阵的一个元素Cov(Xi,Xj)：
\text{Cov}(X_i, Y_i) = \frac{1}{n} \sum_{k=1}^{n} (x_{ki} - \bar{x_i})(x_{ki} - \bar{x_j})
我们可以把这个元素的计算写成矩阵形式，将每一列表示一个特征向量，得到如下形式：
\text{Cov}(X_i, Y_i) = \frac{1}{n}  (X_{i} - \bar{x_i})^T(X_{j} - \bar{x_j})
其中，Xi 是第 i 个特征的列向量，xˉi 是第 i 个特征的均值列向量。
现在我们可以考虑协方差矩阵的计算，可以表示为矩阵乘积的形式：
\boldsymbol{\Sigma}=  \frac{1}{n}  (X_{} - \bar{x})^T(X_{} - \bar{x})
其中，X 是数据矩阵，xˉ 是均值矩阵，每一列表示对应特征的均值。
将 X 展开成列向量形式，我们可以得到：
\boldsymbol{\Sigma}=  \frac{1}{n}  X^TX
这就得到了协方差矩阵的计算公式。需要注意的是，这个公式是在数据已经中心化的基础上进行推导的。
在实际应用中，如果数据没有被中心化，还需要额外的操作来考虑均值的影响。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/889248.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

C++ string类相关用法实例

C++ string类相关用法实例

前言： 1 string是表示字符串的字符串类 2 string类是basic_string模板类的一个实例，它使用char来实例化basic_string模板类，并用char_traits和allocator作为basic_string的默认参数，所以string在底层实际是：basic_str…
阅读更多...
【漏洞修复】OpenSSH-ssh-agent 越权访问CVE-2023-38408

【漏洞修复】OpenSSH-ssh-agent 越权访问CVE-2023-38408

CVE-2023-38408漏洞升级ssh版本 漏洞说明修复步骤RPM包编译 漏洞说明 漏洞名称：OpenSSH-ssh-agent 存在越权访问漏洞影响范围：ssh-agent(-∞, 9.3-p2) openssh(-∞, 9.3p2-1)漏洞描述：SSH-Agent是SSH的一部分，它是一个用于管理私…
阅读更多...
设计模式之享元模式（Flyweight）的C++代码实现

设计模式之享元模式（Flyweight）的C++代码实现

1、享元模式提出 面向对象很好地解决了抽象问题，但是创建对象会带来一定的内存开销。绝大部分情况下，创建对象带来的内存开销是可以忽略不计的；在有些情况下是需要谨慎处理的，如类A的sizeof是50个字节，则创建50*1024*…
阅读更多...
AIGC：从入门到精通

AIGC：从入门到精通

一、前言 相信一部分的人在看到本活动的主题是关于AIGC的时候，都会存在疑惑--到底什么是AIGC呢？故本文主要介绍关于AIGC的基本内容，全部内容采用自己搭建的ChatGPT模型生成，具体内容如下： 本文章，参与&…
阅读更多...
互联网医院|申办互联网医院这些资质不能少

互联网医院|申办互联网医院这些资质不能少

互联网医院作为一种创新的医疗模式，正在以其便捷、智能、人性化的特点改变着人们的生活方式和医疗体验。它以数字化技术和合作共赢的精神，打开了医疗的新纪元。让我们共同期待，互联网医院将为健康事业带来更多机遇和挑战，引领着健…
阅读更多...
Spyglass 脚本

Spyglass 脚本

Spyglass小白可以使用Gui界面进行debug Spyglass检查(一)作为IC设计人员，熟练掌握数字前端语法检查工具Spyglass的重要性不言而喻，本文讲解景芯SoChttps://mp.weixin.qq.com/s/fp07o-AvaQvLT79Di0Tb7A 熟悉电路和软件之后可以使用脚本完成整个流程 sp…
阅读更多...
【分享】使用FileChannel进行文件拷贝

【分享】使用FileChannel进行文件拷贝

前言: 项目实际编写中，使用到了多种文件拷贝方式，有包括专门使用c写了拷贝工具，供给Java调用，也有使用标准的输入输出流，这里分享的是借助 FileChannel 来读写,nio中传送数据使用channelbuffer，大的数据可以…
阅读更多...
第九章 动态规划part09（代码随想录）

第九章 动态规划part09（代码随想录）

198.打家劫舍 题目： 你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。…
阅读更多...
图的顺序存储结构

图的顺序存储结构

目录 图的顺序存储结构 图的顺序存储结构C语言实现 图的邻接表存储结构详解 邻接表计算顶点的出度和入度 图的十字链表存储结构 图的邻接多重表存储结构 图的顺序存储结构 使用图结构表示的数据元素之间虽然具有“多对多”的关系，但是同样可以采用顺序存储&a…
阅读更多...
网络通信原理总结(第五十二课)

网络通信原理总结(第五十二课)

网络通信原理 结构目录 1 TCP/IP协议追层分析物理层(第三十九课)_IHOPEDREAM的博客-CSDN博客 2 网络通信TCP/IP协议逐层分析数据链路层(第四十课)_IHOPEDREAM的博客-CSDN博客 3 网络通信原理数据链路层&数制转换(第四十一课)_IHOPEDREAM的博客-CSDN博客 4 网络通信原理…
阅读更多...
[LeetCode]矩阵对角线元素的和

[LeetCode]矩阵对角线元素的和

解题 思路 1: 循环,找到主对角线的下标和副对角线的下标,如果矩阵长或宽为奇数的时候,需要减去中间公共的那一个值,中间公共的那个数的下标为mat[mat.size()/2][mat.size()/2]副对角线的下标为 mat [i][mat.size()-i-1] class Solution { public:int diagonalSum(vector<ve…
阅读更多...
一文读懂｜Linux 虚拟文件系统（VFS）

一文读懂｜Linux 虚拟文件系统（VFS）

前言 虚拟文件系统是一个很庞大的架构&#xff0c;如果要分析的面面俱到&#xff0c;会显得特别复杂而笨拙&#xff0c;让人看着看着&#xff0c;就不知所云了&#xff08;当然主要还是笔者太菜&#xff09;&#xff0c;所以这篇博客&#xff0c;以 open() 函数为切入点&#…
阅读更多...
2020年3月全国计算机等级考试真题（C语言二级）

2020年3月全国计算机等级考试真题（C语言二级）

2020年3月全国计算机等级考试真题&#xff08;C语言二级&#xff09; 第1题 有以下程序 void fun1 (char*p) { char*q; qp; while(*q!\0) { (*Q); q&#xff1b; } } main() { char a[]{"Program"},*p; p&a[3]; fun1(p); print…
阅读更多...
英语学习 Eudic欧路词典 for Mac

英语学习 Eudic欧路词典 for Mac

欧路词典是一款功能强大的英语学习工具&#xff0c;其多语种支持、海量词库、强大的翻译功能、听力训练和生词本和笔记等特点&#xff0c;使得用户可以方便地进行英语学习和提高英语水平&#xff0c;适用于各种英语学习人员和文化交流人员等不同人群。 1 、全面支持最新Retina…
阅读更多...
Salesforce Winter ‘24即将发布！亮点功能抢先看

Salesforce Winter ‘24即将发布！亮点功能抢先看

随着Winter 24脚步的临近&#xff0c;一波增强功能即将面世&#xff0c;Trailblazers的期望值越来越高。在这片云计算的海洋里&#xff0c;一些亮点功能总能在生态系统中引起巨大轰动。 Winter 24发布日期 Winter 24发布的具体日期取决于您的Salesforce实例&#xff0c;主要日…
阅读更多...
vue echarts macd指标 完整代码

vue echarts macd指标 完整代码

1 逻辑 给指定的series两个对象 两个对象有相同的xAxisIndex: 2,yAxisIndex: 2, 不同的data {name: "",type: "line",data: data1,xAxisIndex: 2,yAxisIndex: 2,},{name: "",type: "bar",data: data2,xAxisIndex: 2,yAxisIndex: 2,},…
阅读更多...
爱荷华州的一个学区正在使用ChatGPT来决定禁止哪些书籍

爱荷华州的一个学区正在使用ChatGPT来决定禁止哪些书籍

为了响应爱荷华州最近颁布的立法&#xff0c;管理员们正在从梅森市学校图书馆移除禁书&#xff0c;官员们正在使用ChatGPT帮助他们挑选书籍&#xff0c;根据公报和大众科学. 由州长金雷诺兹签署的禁令背后的新法律是教育改革浪潮的一部分&#xff0c;共和党立法者认为这是保护…
阅读更多...
滑块验证码-接口返回base64数据

滑块验证码-接口返回base64数据

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录 前言所需包图片示例使用方法提示前言 滑动验证码在实际爬虫开发过程中会遇到很多，不同网站返回的数据也是千奇百怪。这里分享一种接口返回base64格式的情况以及处理方式 所需包 opencv-python、…
阅读更多...
【LangChain】Feature Store 特征库 一种新型存储方式 —— 功能存储

【LangChain】Feature Store 特征库 一种新型存储方式 —— 功能存储

Feature Store 特征库 特征库的主要目的是什么&#xff1f;特征库的五个主要组件组成一&#xff1a;Serving 服务组成二&#xff1a;Storage 存储组成三&#xff1a;Transform 转换组成四&#xff1a;Monitoring 监控组成五&#xff1a;Feature Registry 功能注册表 Feature St…
阅读更多...
简单学习MySQL

简单学习MySQL

最近&#xff0c;再看数据库相关的知识&#xff0c;用不着学太深&#xff0c;先学一些基本知识&#xff0c;以后需要的时候有个基础&#xff0c;不至于像个无头苍蝇&#xff0c;我学习的网站如下&#xff08;MySQL 教程 | 菜鸟教程 (runoob.com)&#xff09; 对MySQL的介绍 My…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023