目录

图的顺序存储结构

图的顺序存储结构C语言实现

图的邻接表存储结构详解

邻接表计算顶点的出度和入度

图的十字链表存储结构

图的邻接多重表存储结构

---

图的顺序存储结构

使用图结构表示的数据元素之间虽然具有“多对多”的关系，但是同样可以采用顺序存储，也就是使用数组有效地存储图。

使用数组存储图时，需要使用两个数组，一个数组存放图中顶点本身的数据（一维数组），另外一个数组用于存储各顶点之间的关系（二维数组）。

存储图中各顶点本身数据，使用一维数组就足够了；存储顶点之间的关系时，要记录每个顶点和其它所有顶点之间的关系，所以需要使用二维数组。

不同类型的图，存储的方式略有不同，根据图有无权，可以将图划分为两大类：图和网 。

图，包括无向图和有向图；

网，是指带权的图，包括无向网和有向网。

存储方式的不同，指的是：在使用二维数组存储图中顶点之间的关系时，如果顶点之间存在边或弧，在相应位置用 1 表示，反之用 0 表示；如果使用二维数组存储网中顶点之间的关系，顶点之间如果有边或者弧的存在，在数组的相应位置存储其权值；反之用 0 表示。

结构代码表示：

1. #define MAX_VERtEX_NUM 20 //顶点的最大个数
2. #define VRType int //表示顶点之间的关系的变量类型
3. #define InfoType char //存储弧或者边额外信息的指针变量类型
4. #define VertexType int //图中顶点的数据类型
5. typedef enum{DG,DN,UDG,UDN}GraphKind; //枚举图的 4 种类型
6. typedef struct {
7. VRType adj; //对于无权图，用 1 或 0 表示是否相邻；对于带权图，直接为权值。
8. InfoType * info; //弧或边额外含有的信息指针
9. }ArcCell,AdjMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM];
11. typedef struct {
12. VertexType vexs[MAX_VERtEX_NUM]; //存储图中顶点数据
13. AdjMatrix arcs; //二维数组，记录顶点之间的关系
14. int vexnum,arcnum; //记录图的顶点数和弧（边）数
15. GraphKind kind; //记录图的种类
16. }MGraph;

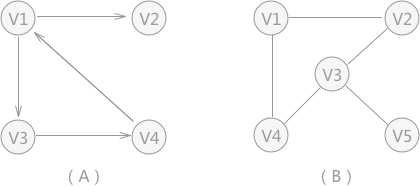
图1 有向图和无向图

例如，存储图 1 中的无向图（B）时，除了存储图中各顶点本身具有的数据外，还需要使用二维数组存储任意两个顶点之间的关系。

由于 （B） 为无向图，各顶点没有权值，所以如果两顶点之间有关联，相应位置记为 1 ；反之记为 0 。构建的二维数组如图 2 所示。

 

图2 无向图对应的二维数组arcs

在此二维数组中，每一行代表一个顶点，依次从 V1 到 V5 ，每一列也是如此。比如 arcs[0][1] = 1 ，表示 V1 和 V2 之间有边存在；而 arcs[0][2] = 0，说明 V1 和 V3 之间没有边。

对于无向图来说，二维数组构建的二阶矩阵，实际上是对称矩阵，在存储时就可以采用压缩存储的方式存储下三角或者上三角。

通过二阶矩阵，可以直观地判断出各个顶点的度，为该行（或该列）非 0 值的和。例如，第一行有两个 1，说明 V1 有两个边，所以度为 2。

存储图 1 中的有向图（A）时，对应的二维数组如图 3 所示：

 

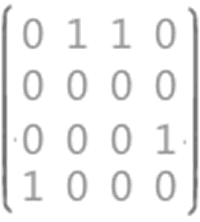
图 3 有向图对应的二维数组arcs

例如，arcs[0][1] = 1 ，证明从 V1 到 V2 有弧存在。且通过二阶矩阵，可以很轻松得知各顶点的出度和入度，出度为该行非 0 值的和，入度为该列非 0 值的和。例如，V1 的出度为第一行两个 1 的和，为 2 ； V1 的入度为第一列中 1 的和，为 1 。所以 V1 的出度为 2 ，入度为 1 ，度为两者的和 3 。

图的顺序存储结构C语言实现

1. #include <stdio.h>
2. #define MAX_VERtEX_NUM 20 //顶点的最大个数
3. #define VRType int //表示顶点之间的关系的变量类型
4. #define InfoType char //存储弧或者边额外信息的指针变量类型
5. #define VertexType int //图中顶点的数据类型
6. typedef enum{DG,DN,UDG,UDN}GraphKind; //枚举图的 4 种类型
7. typedef struct {
8. VRType adj; //对于无权图，用 1 或 0 表示是否相邻；对于带权图，直接为权值。
9. InfoType * info; //弧或边额外含有的信息指针
10. }ArcCell,AdjMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM];
12. typedef struct {
13. VertexType vexs[MAX_VERtEX_NUM]; //存储图中顶点数据
14. AdjMatrix arcs; //二维数组，记录顶点之间的关系
15. int vexnum,arcnum; //记录图的顶点数和弧（边）数
16. GraphKind kind; //记录图的种类
17. }MGraph;
18. //根据顶点本身数据，判断出顶点在二维数组中的位置
19. int LocateVex(MGraph * G,VertexType v){
20. int i=0;
21. //遍历一维数组，找到变量v
22. for (; i<G->vexnum; i++) {
23. if (G->vexs[i]==v) {
24. break;
25. }
26. }
27. //如果找不到，输出提示语句，返回-1
28. if (i>G->vexnum) {
29. printf("no such vertex.\n");
30. return -1;
31. }
32. return i;
33. }
34. //构造有向图
35. void CreateDG(MGraph *G){
36. //输入图含有的顶点数和弧的个数
37. scanf("%d,%d",&(G->vexnum),&(G->arcnum));
38. //依次输入顶点本身的数据
39. for (int i=0; i<G->vexnum; i++) {
40. scanf("%d",&(G->vexs[i]));
41. }
42. //初始化二维矩阵，全部归0，指针指向NULL
43. for (int i=0; i<G->vexnum; i++) {
44. for (int j=0; j<G->vexnum; j++) {
45. G->arcs[i][j].adj=0;
46. G->arcs[i][j].info=NULL;
47. }
48. }
49. //在二维数组中添加弧的数据
50. for (int i=0; i<G->arcnum; i++) {
51. int v1,v2;
52. //输入弧头和弧尾
53. scanf("%d,%d",&v1,&v2);
54. //确定顶点位置
55. int n=LocateVex(G, v1);
56. int m=LocateVex(G, v2);
57. //排除错误数据
58. if (m==-1 ||n==-1) {
59. printf("no this vertex\n");
60. return;
61. }
62. //将正确的弧的数据加入二维数组
63. G->arcs[n][m].adj=1;
64. }
65. }
66. //构造无向图
67. void CreateDN(MGraph *G){
68. scanf("%d,%d",&(G->vexnum),&(G->arcnum));
69. for (int i=0; i<G->vexnum; i++) {
70. scanf("%d",&(G->vexs[i]));
71. }
72. for (int i=0; i<G->vexnum; i++) {
73. for (int j=0; j<G->vexnum; j++) {
74. G->arcs[i][j].adj=0;
75. G->arcs[i][j].info=NULL;
76. }
77. }
78. for (int i=0; i<G->arcnum; i++) {
79. int v1,v2;
80. scanf("%d,%d",&v1,&v2);
81. int n=LocateVex(G, v1);
82. int m=LocateVex(G, v2);
83. if (m==-1 ||n==-1) {
84. printf("no this vertex\n");
85. return;
86. }
87. G->arcs[n][m].adj=1;
88. G->arcs[m][n].adj=1;//无向图的二阶矩阵沿主对角线对称
89. }
90. }
91. //构造有向网，和有向图不同的是二阶矩阵中存储的是权值。
92. void CreateUDG(MGraph *G){
93. scanf("%d,%d",&(G->vexnum),&(G->arcnum));
94. for (int i=0; i<G->vexnum; i++) {
95. scanf("%d",&(G->vexs[i]));
96. }
97. for (int i=0; i<G->vexnum; i++) {
98. for (int j=0; j<G->vexnum; j++) {
99. G->arcs[i][j].adj=0;
100. G->arcs[i][j].info=NULL;
101. }
102. }
103. for (int i=0; i<G->arcnum; i++) {
104. int v1,v2,w;
105. scanf("%d,%d,%d",&v1,&v2,&w);
106. int n=LocateVex(G, v1);
107. int m=LocateVex(G, v2);
108. if (m==-1 ||n==-1) {
109. printf("no this vertex\n");
110. return;
111. }
112. G->arcs[n][m].adj=w;
113. }
114. }
115. //构造无向网。和无向图唯一的区别就是二阶矩阵中存储的是权值
116. void CreateUDN(MGraph* G){
117. scanf("%d,%d",&(G->vexnum),&(G->arcnum));
118. for (int i=0; i<G->vexnum; i++) {
119. scanf("%d",&(G->vexs[i]));
120. }
121. for (int i=0; i<G->vexnum; i++) {
122. for (int j=0; j<G->vexnum; j++) {
123. G->arcs[i][j].adj=0;
124. G->arcs[i][j].info=NULL;
125. }
126. }
127. for (int i=0; i<G->arcnum; i++) {
128. int v1,v2,w;
129. scanf("%d,%d,%d",&v1,&v2,&w);
130. int m=LocateVex(G, v1);
131. int n=LocateVex(G, v2);
132. if (m==-1 ||n==-1) {
133. printf("no this vertex\n");
134. return;
135. }
136. G->arcs[n][m].adj=w;
137. G->arcs[m][n].adj=w;//矩阵对称
138. }
139. }
140. void CreateGraph(MGraph *G){
141. //选择图的类型
142. scanf("%d",&(G->kind));
143. //根据所选类型，调用不同的函数实现构造图的功能
144. switch (G->kind) {
145. case DG:
146. return CreateDG(G);
147. break;
148. case DN:
149. return CreateDN(G);
150. break;
151. case UDG:
152. return CreateUDG(G);
153. break;
154. case UDN:
155. return CreateUDN(G);
156. break;
157. default:
158. break;
159. }
160. }
161. //输出函数
162. void PrintGrapth(MGraph G)
163. {
164. for (int i = 0; i < G.vexnum; i++)
165. {
166. for (int j = 0; j < G.vexnum; j++)
167. {
168. printf("%d ", G.arcs[i][j].adj);
169. }
170. printf("\n");
171. }
172. }
173. int main() {
174. MGraph G;//建立一个图的变量
175. CreateGraph(&G);//调用创建函数，传入地址参数
176. PrintGrapth(G);//输出图的二阶矩阵
177. return 0;
178. }

注意：在此程序中，构建无向网和有向网时，对于之间没有边或弧的顶点，相应的二阶矩阵中存放的是 0。目的只是为了方便查看运行结果，而实际上如果顶点之间没有关联，它们之间的距离应该是无穷大（∞）。

例如，使用上述程序存储图 4（a）的有向网时，存储的两个数组如图 4（b）所示：

 

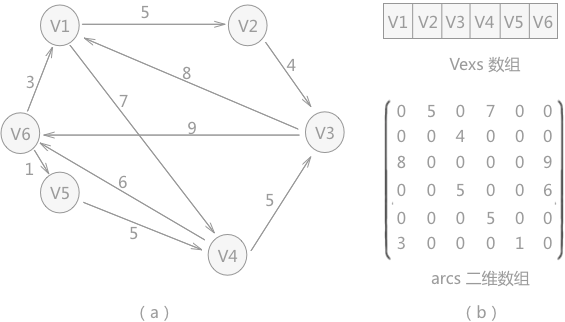
图 4 有向网

相应地运行结果为：

2
6,10
1
2
3
4
5
6
1,2,5
2,3,4
3,1,8
1,4,7
4,3,5
3,6,9
6,1,3
4,6,6
6,5,1
5,4,5
0 5 0 7 0 0
0 0 4 0 0 0
8 0 0 0 0 9
0 0 5 0 0 6
0 0 0 5 0 0
3 0 0 0 1 0

总结一下，本节主要详细介绍了使用数组存储图的方法，在实际操作中使用更多的是链式存储结构，例如邻接表、十字链表和邻接多重表

图的邻接表存储结构详解

通常，图更多的是采用链表存储，具体的存储方法有 3 种，分别是邻接表、邻接多重表和十字链表。

本节先讲解图的邻接表存储法。邻接表既适用于存储无向图，也适用于存储有向图。

在具体讲解邻接表存储图的实现方法之前，先普及一个"邻接点"的概念。在图中，如果两个点相互连通，即通过其中一个顶点，可直接找到另一个顶点，则称它们互为邻接点。

邻接指的是图中顶点之间有边或者弧的存在。

邻接表存储图的实现方式是，给图中的各个顶点独自建立一个链表，用节点存储该顶点，用链表中其他节点存储各自的临界点。

与此同时，为了便于管理这些链表，通常会将所有链表的头节点存储到数组中（也可以用链表存储）。也正因为各个链表的头节点存储的是各个顶点，因此各链表在存储临界点数据时，仅需存储该邻接顶点位于数组中的位置下标即可。

例如，存储图 1a) 所示的有向图，其对应的邻接表如图 1b) 所示：

 

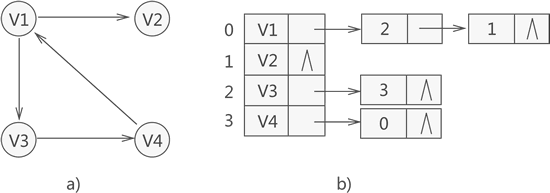
图 1 邻接表存储有向图

拿顶点 V1 来说，与其相关的邻接点分别为 V2 和 V3，因此存储 V1 的链表中存储的是 V2 和 V3 在数组中的位置下标 1 和 2。

从图 1 中可以看出，存储各顶点的节点结构分为两部分，数据域和指针域。数据域用于存储顶点数据信息，指针域用于链接下一个节点，如图 2 所示：

 

图 2 邻接表节点结构

在实际应用中，除了图 2 这种节点结构外，对于用链接表存储网（边或弧存在权）结构，还需要节点存储权的值，因此需使用图 3 中的节点结构：

 

图 3 邻接表存储网结构使用的节点

图 1 中的链接表结构转化为对应 C 语言代码如下：

1. #define MAX_VERTEX_NUM 20//最大顶点个数
2. #define VertexType int//顶点数据的类型
3. #define InfoType int//图中弧或者边包含的信息的类型
4. typedef struct ArcNode{
5. int adjvex;//邻接点在数组中的位置下标
6. struct ArcNode * nextarc;//指向下一个邻接点的指针
7. InfoType * info;//信息域
8. }ArcNode;
9. typedef struct VNode{
10. VertexType data;//顶点的数据域
11. ArcNode * firstarc;//指向邻接点的指针
12. }VNode,AdjList[MAX_VERTEX_NUM];//存储各链表头结点的数组
13. typedef struct {
14. AdjList vertices;//图中顶点的数组
15. int vexnum,arcnum;//记录图中顶点数和边或弧数
16. int kind;//记录图的种类
17. }ALGraph;

邻接表计算顶点的出度和入度

使用邻接表计算无向图中顶点的入度和出度会非常简单，只需从数组中找到该顶点然后统计此链表中节点的数量即可。

而使用邻接表存储有向图时，通常各个顶点的链表中存储的都是以该顶点为弧尾的邻接点，因此通过统计各顶点链表中的节点数量，只能计算出该顶点的出度，而无法计算该顶点的入度。

对于利用邻接表求某顶点的入度，有两种方式：

1. 遍历整个邻接表中的节点，统计数据域与该顶点所在数组位置下标相同的节点数量，即为该顶点的入度；
2. 建立一个逆邻接表，该表中的各顶点链表专门用于存储以此顶点为弧头的所有顶点在数组中的位置下标。比如说，建立一张图 1a) 对应的逆邻接表，如图 4 所示：

 

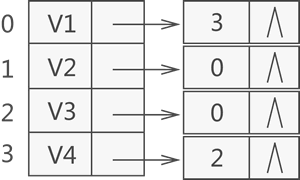
图 4 逆邻接表示意图

对于具有 n 个顶点和 e 条边的无向图，邻接表中需要存储 n 个头结点和 2e 个表结点。在图中边或者弧稀疏的时候，使用邻接表要比前一节介绍的邻接矩阵更加节省空间。

图的十字链表存储结构

与邻接表不同，十字链表法仅适用于存储有向图和有向网。不仅如此，十字链表法还改善了邻接表计算图中顶点入度的问题。

十字链表存储有向图（网）的方式与邻接表有一些相同，都以图（网）中各顶点为首元节点建立多条链表，同时为了便于管理，还将所有链表的首元节点存储到同一数组（或链表）中。

其中，建立个各个链表中用于存储顶点的首元节点结构如图 1 所示：

 

图 1 十字链表中首元节点结构示意图

从图 1 可以看出，首元节点中有一个数据域和两个指针域（分别用 firstin 和 firstout 表示）：

• firstin 指针用于连接以当前顶点为弧头的其他顶点构成的链表；
• firstout 指针用于连接以当前顶点为弧尾的其他顶点构成的链表；
• data 用于存储该顶点中的数据；

由此可以看出，十字链表实质上就是为每个顶点建立两个链表，分别存储以该顶点为弧头的所有顶点和以该顶点为弧尾的所有顶点。

注意，存储图的十字链表中，各链表中首元节点与其他节点的结构并不相同，图 1 所示仅是十字链表中首元节点的结构，链表中其他普通节点的结构如图 2 所示：

 

图 2 十字链表中普通节点的结构示意图

从图 2 中可以看出，十字链表中普通节点的存储分为 5 部分内容，它们各自的作用是：

• tailvex 用于存储以首元节点为弧尾的顶点位于数组中的位置下标；
• headvex 用于存储以首元节点为弧头的顶点位于数组中的位置下标；
• hlink 指针：用于链接下一个存储以首元节点为弧头的顶点的节点；
• tlink 指针：用于链接下一个存储以首元节点为弧尾的顶点的节点；
• info 指针：用于存储与该顶点相关的信息，例如量顶点之间的权值；

比如说，用十字链表存储图 3a) 中的有向图，存储状态如图 3b) 所示：

 

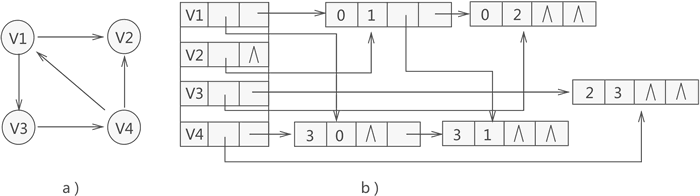
图 3 十字链表存储有向图示意图

拿图 3 中的顶点 V1 来说，通过构建好的十字链表得知，以该顶点为弧头的顶点只有存储在数组中第 3 位置的 V4（因此该顶点的入度为 1），而以该顶点为弧尾的顶点有两个，分别为存储数组第 1 位置的 V2 和第 2 位置的 V3（因此该顶点的出度为 2）。

对于图 3 各个链表中节点来说，由于表示的都是该顶点的出度或者入度，因此没有先后次序之分。

图的邻接多重表存储结构

为了提高在无向图中操作顶点的效率，本节学习一种新的适用于存储无向图的方法——邻接多重表。

注意，邻接多重表仅适用于存储无向图或无向网。

邻接多重表存储无向图的方式，可看作是邻接表和十字链表的结合。同邻接表和十字链表存储图的方法相同，都是独自为图中各顶点建立一张链表，存储各顶点的节点作为各链表的首元节点，同时为了便于管理将各个首元节点存储到一个数组中。各首元节点结构如图 1 所示：

 

图 1 邻接多重表各首元节点的结构示意图

图 1 中各区域及其功能为：

• data：存储此顶点的数据；
• firstedge：指针域，用于指向同该顶点有直接关联的存储其他顶点的节点。

从图 1 可以看到，邻接多重表采用与邻接表相同的首元节点结构。但各链表中其他节点的结构与十字链表中相同，如图 2 所示：

 

图 2 邻接多重表中其他节点结构

图 2 节点中各区域及功能如下：

• mark：标志域，用于标记此节点是否被操作过，例如在对图中顶点做遍历操作时，为了防止多次操作同一节点，mark 域为 0 表示还未被遍历；mark 为 1 表示该节点已被遍历；
• ivex 和 jvex：数据域，分别存储图中各边两端的顶点所在数组中的位置下标；
• ilink：指针域，指向下一个存储与 ivex 有直接关联顶点的节点；
• jlink：指针域，指向下一个存储与 jvex 有直接关联顶点的节点；
• info：指针域，用于存储与该顶点有关的其他信息，比如无向网中各边的权；

综合以上信息，如果我们想使用邻接多重表存储图 3a) 中的无向图，则与之对应的邻接多重表如图 3b) 所示：

 

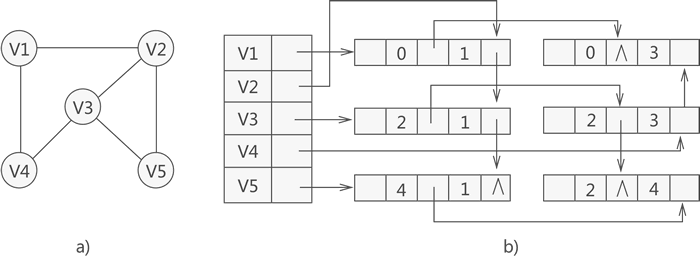
图 3 无向图及其对应的邻接多重表

从图 3 中，可直接找到与各顶点有直接关联的其他顶点。比如说，与顶点 V1 有关联的顶点为存储在数组下标 1 处的 V2 和数组下标 3 处的 V4，而与顶点 V2 有关联的顶点有 3 个，分别是 V1、V3 和 V5。