参考文献：

[1]邓红卫. 计及碳排放成本的电—气—热综合能源系统节点能价计算方法研究[D].东北电力大学,2019.

[2]王静,徐箭,廖思阳,司马莉萍,孙元章,魏聪颖.计及新能源出力不确定性的电气综合能源系统协同优化[J].电力系统自动化,2019,43(15):2-9.

[3]郑豪丰,杨国华,潘欢,胡瑞琨,邹玙琦,易俊超.考虑区域供热系统及不确定性因素的综合能源系统日前调度[J].电力系统及其自动化学报,2020,32(08):83-90.

一、电力系统（直流潮流即可）

        直流潮流法的特点是用电力系统的交流潮流（有功功率和无功功率）等值的直流电流来代替。甚至只用直流电路的解析法来分析电力系统的有功潮流，而不考虑无功分布对有功的影响。这样一来计算速度加快，但计算的准确度有所降低，本方法适用于对潮流计算准确度要求不高的计算场景。

        下面先对直流潮流法的原理进行简单介绍：

        上图为直流法的等值图，在上图所示的输电线路中，有功潮流为： 

        为了快速计算的需要，将上式进行了三项简化：
        （1）考虑一般高压电网中线路的电阻远小于电抗，对地电导也可以忽略即 Gii=0 Gij =0
        （2）按照标幺值计算时，节点电压与其额定电压相差不大，故有：Ui≈Uj≈1.0；
        （3）线路两端的电压相角差（θi-θj）较小，所以有： 

        这样，上式前两项均为零，只剩第三项 

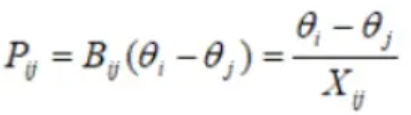
        这就相当于线路两端的直流电位分别为θi和θj。线路的直流电阻是Xij。则用矩阵表示为如下式所示。 

        式中：B0为正常运行时网络的节点电纳矩阵；θ为网络中各节点的电压相位角的向量；P为节点注入的有功功率向量​。 

二、天然气系统

2.1天然气系统模型

 

（压缩比取值1.5）

2.2天然气管道模型 

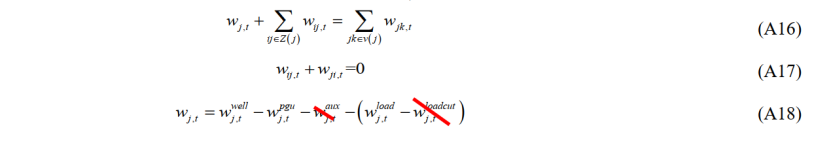
        由于天然气流量方程是非线性的，因此要对其进行线性化处理。对方程进行变形之后进行分段线性化。

        分段m=50（管道流量方向的前提下）；如果不知道流量的 m=100，在一、三象限各50。

（文献cajP18-P19也有weymouth方程的分段线性化处理，方法一样。）

三、热力系统模型

3.1热源模型

        热源主要是CHP机组（燃气轮机、余热锅炉）与电锅炉。

3.1.1 CHP机组模型

        CHP机组的效率以及容量与爬坡限制如下图所示（来自其他文献，只用效率即可）：

 

 

 

燃气轮机的天然气消耗量： 

 

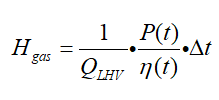
 3.1.2 电锅炉模型

3.2 热网模型

 

 

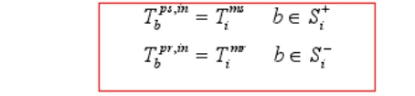
 3.3 复杂的管道流量损失转化 

四、目标函数

 

 

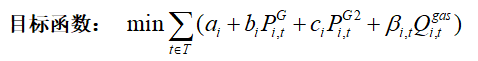
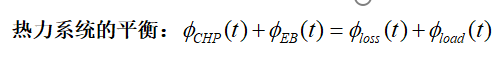
4.1 模型及相关数据 

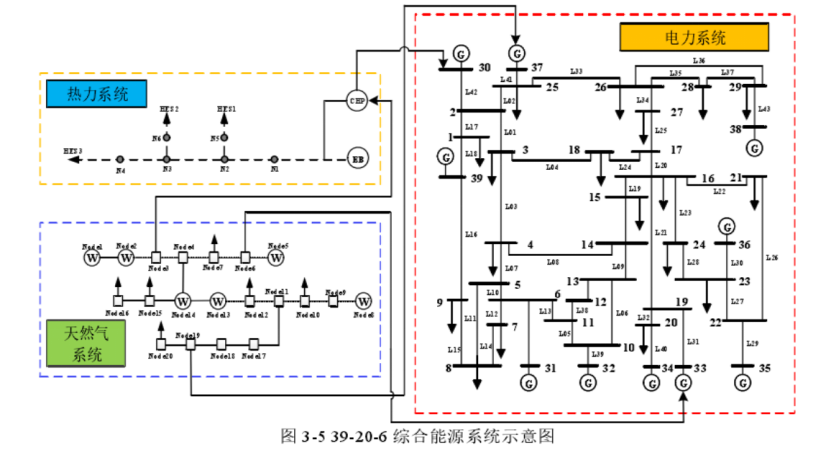
4.1.1 电力数据

        （二阶锥模型，数据与matpower39节点相同，其中2台发电机改成燃气发电机）

总共10台发电机组，总装机容量6967MW，总电力负荷5941.5MW。

电网节点33	燃气轮机	气网节点6供气
电网节点37	燃气轮机	气网节点19供气
电网节点30	CHP机组	气网节点3供气	是热网节点1的热源
其余7个电源节点	燃煤机组

 

 

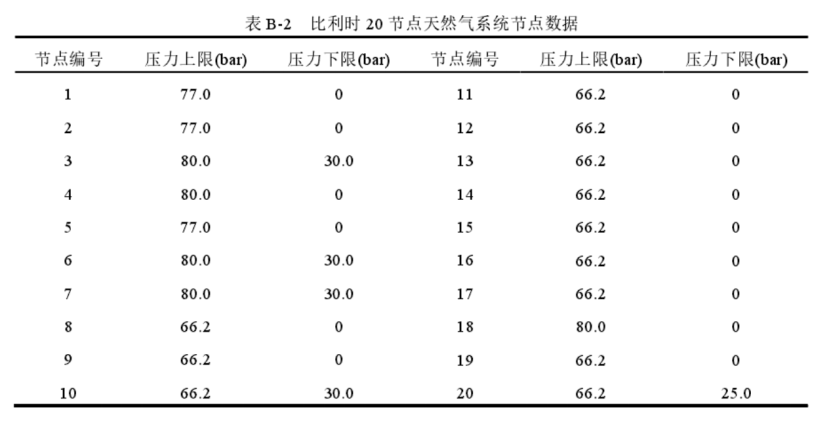
4.1.2 天然气系统数据

        总共6个气源，9个燃气负荷。7个常规燃气负荷，2个燃机发电机负荷。总负荷2.4608Mm³。1-3#的成本为0.085美元/m3，4-6#电成本为0.062美元/m³。

4.1.3 热力系统相关数据

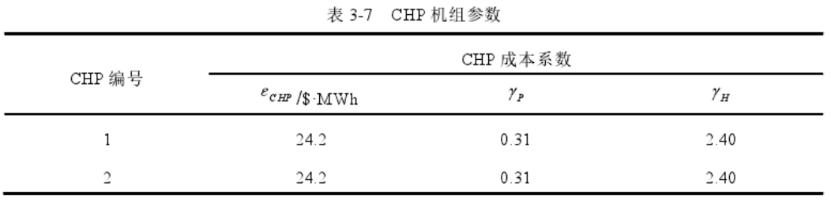
        1台CHP机组，1台电锅炉和三个热负荷。总负荷为50MW，其中电锅炉电热比系数为0.8，出力上限为30MW。CHP机组的基本参数如下图。

 

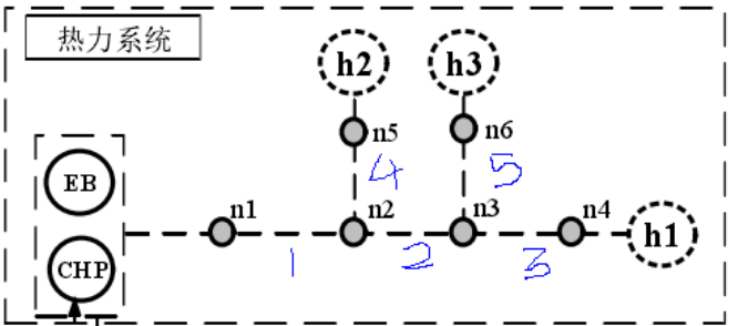
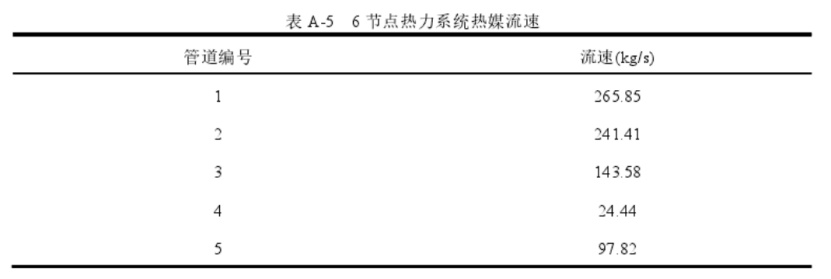
热力系统支路	起始节点	终止节点
1	1	2
2	2	3
3	3	4
4	2	5
5	3	6

 

五、代码获取

【免费】电-气-热综合能源系统优化调度matlab代码