1.旋转矩阵
1.1内积

1.2外积

1.3坐标系间的欧式变换
相机运动是一个刚体运动,它保证了同一个向量在各个坐标系下的长度和夹角都不会 发生变化。这种变换称为欧氏变换。
旋转矩阵:它是一个行列式为 1 的正交矩阵。

旋转矩阵为正交阵,它的逆(即转置)描述了一个相反的旋转。
加上平移:

1.4变换矩阵与齐次坐标

关于变换矩阵 T,它具有比较特别的结构:左上角为旋转矩阵,右侧为平移向量,左 下角为 0 向量,右下角为 1。这种矩阵又称为特殊欧氏群(Special Euclidean Group):
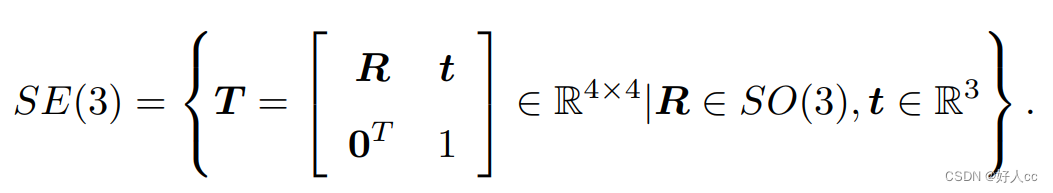
求解该矩阵的逆表示一个反向的变换:
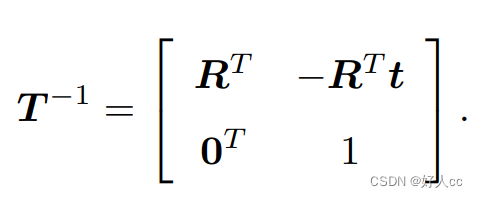
2.Eigen库---线性代数库
#include <Eigen/Core> //核心部分
#include <Eigen/Dense> //稠密矩阵的代数运算(逆、特征值等)
using namespace Eigen;
//所有的向量,矩阵都是
Matrix<数据类型,行,列>
Vector3d实质是 Matrix<double,3,1>
可以直接求逆 QR分解 cholesky分解Eigen对数据类型转换严格,可以通过显示转换来完成转换。