本文内容借鉴一本我非常喜欢的书——《数据结构与算法图解》。学习之余,我决定把这本书精彩的部分摘录出来与大家分享。
基础数据结构:数组
数组是计算机科学中最基本的数据结构之一。如果你用过数组,那么应该知道它就是一个含有
数据的列表。它有多种用途,适用于各种场景,下面就举个简单的例子。
在一个超市的应用软件中,其源代码可能会包含以下片段:
char* array[] = { "apples", "bananas", "cucumbers", "dates", "elderberries" };这就是一个数组,它刚好包含 5 个字符串,每个代表我会从超市买的食物。
此外,我们会用一些名为索引的数字来标识每项数据在数组中的位置。
在大多数的编程语言中,索引是从 0 算起的,因此在这个例子中, "apples" 的索为
0,"elderberries" 的索引为 4,如下所示。

若想了解某个数据结构(例如数组、集合、链表、栈和队列)的性能,得分析程序怎样操作这一
数据结构。一般数据结构都有以下 4种操作。
①读取:查看数据结构中某一位置上的数据。
② 查找:从数据结构中找出某个数据值的所在。
③插入:给数据结构增加一个数据值。
④删除:从数据结构中移走一个数据值。
本章我们将会研究这些操作在数组上的运行速度。
请切记贯穿本书的一个重要理论: 操作的速度并不按照时间计算,而是按照步数计算。
为什么呢?
简单理解为:同样的一个操作,在我这用了好久的二手笔记本上可能需要跑10秒,但在一台超级量
子计算机上可能用“一瞬间”的时间。
所以,评估一个操作的快慢不能依赖于运行时间,而是它操作的步数。
此外,操作的速度,又称为时间复杂度。
接下来我们就一起看看上述四种操作在数组上要花费多少步。
1.读取
读取,即查看数组中某个索引所指的数据值。
这只要一步就够了,因为计算机本身就有跳到任一索引位置的能力。
例如:
printf("%s\n", array[0]);//打印数组索引0处的值,其值应为apples
printf("%s\n", array[2]);//打印数组索引2处的值,其值应为cucumbers计算机为什么能一步到位呢?原因如下。
计算机的内存可以被看成一堆格子,格子中的数字代表每个格子的地址编号(就像宿舍楼里,每个
宿舍都有各自的宿舍号),且这些地址是连续的。
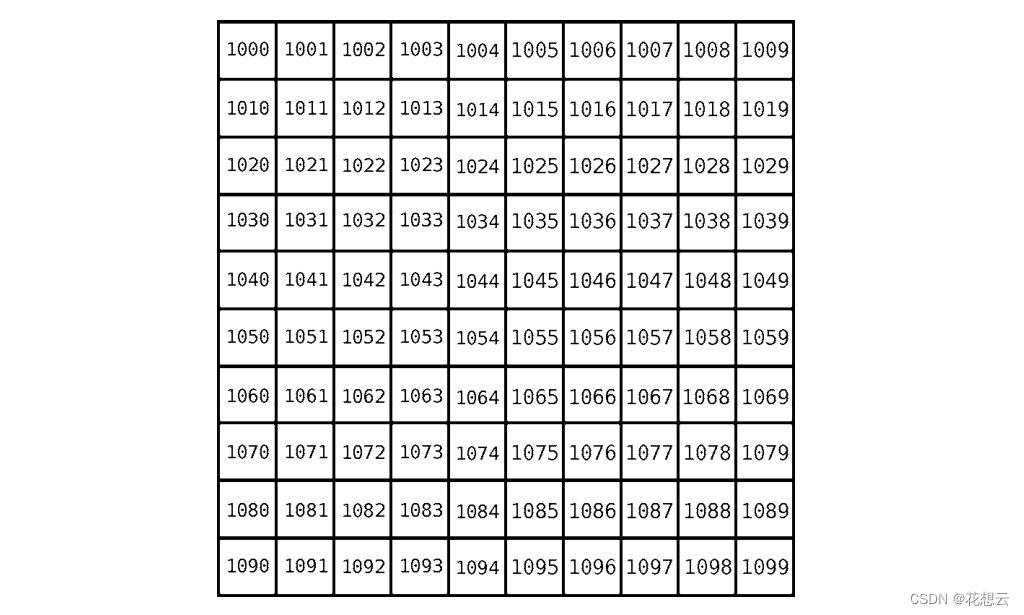
当程序声明一个数组时,它会先划分出一些连续的空格子以备使用。换句话说,如果你想创建一个
包含 5个元素的数组,计算机就会找出 5个排成一行的空格子,将其当成数组。

购物清单数组的索引和内存地址,如下图所示。

计算机之所以在读取数组中某个索引所指的值时,能直接跳到那个位置上,是因为它具备以下条件。
(1) 计算机可以一步就跳到任意一个内存地址上。(就好比,要是你知道大街 123号在哪儿,那么就可以直奔过去。
(2) 数组本身会记有第一个格子的内存地址,因此,计算机知道这个数组的开头在哪里。
(3) 数组的索引从 0算起。
回到刚才的例子,当我们叫计算机读取索引 2 的值时,它会做以下演算。
(1) 该数组的索引从 0算起,其开头的内存地址为 1010。
(2) 索引 2 在索引 0 后的第 2 个格子上。
(3) 于是索引 2 的内存地址为 1012,因为 1010 + 2 = 1012。
当计算机一步跳到 1013时,我们就能获取到 "cucumbers" 这个值了。
所以,数组的读取是一种非常高效的操作,因为它只要一步就好。一步自然也是最快的速度。
这种一步读取任意索引的能力,也是数组好用的原因之一。
2.查找
如前所述,对于数组来说,查找就是检查它是否包含某个值,如果包含,还得给出其索引。那么,
我们就试试在数组中查找 "dates" 要用多少步。
对于我们人来说,可以一眼就看到这个购物清单上的 "dates" ,并数出它的索引为 3。
但是,计算机并没有眼睛,它只能一步一步地检查整个数组。想要查找数组中是否存在某个值,计
算机会先从索引 0开始,检查其值,如果不匹配,则继续下一个索引,以此类推,直至找到为止。
我们用以下图来演示计算机如何从购物清单中查找 "dates" 。
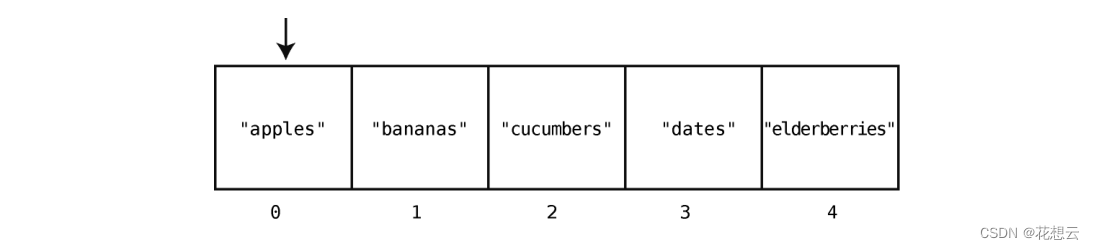
首先,计算机检查索引 0。
因为索引 0的值是 "apples" ,并非我们所要的 "dates" ,所以计算机跳到下一个索引上。
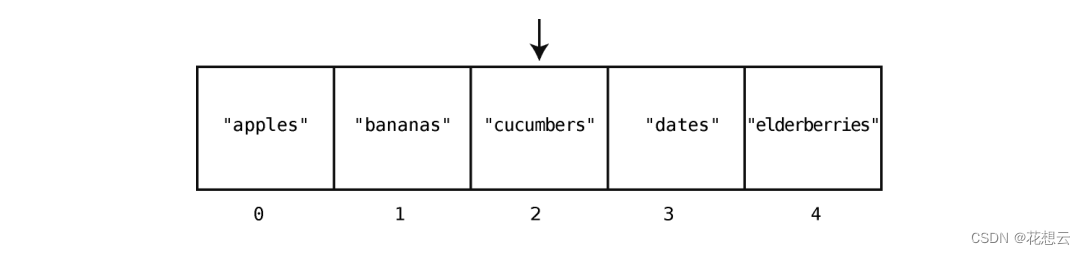
索引 1也不是 "dates" ,于是计算机再跳到索引 2。
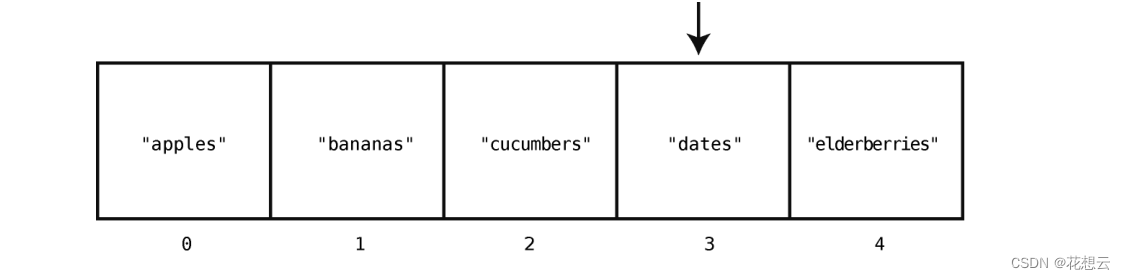
但索引 2 的值仍不匹配,计算机只好再跳到下一格。
到此为止,"dates"已经被找到,我们返回它的值以及它的索引 3 。
在这个例子中,因为我们检查了 4个格子才找到想要的值,所以这次操作总计是 4步。
这种逐个格子去检查的做法,就是最基本的查找方法——线性查找。
到此为止,我们再思考一下,在数组上进行线性查找最多要多少步呢?
如果我们要找的值刚好在数组的最后一个格子里(如本例的 elderberries ),那么计算机从头到尾
检查每个格子,会在最后才找到。
同样,如果我们要找的值并不存在于数组中,那么计算机也还是得查遍每个格子,才能确定这个值
不在数组中。
于是,一个 5格的数组,其线性查找的步数最大值是 5,而对于一个 500格的数组,则是 500。
以此类推,一个 N格的数组,其线性查找的最多步数是 N(N可以是任何自然数)。
可见,无论是多长的数组,查找都比读取要慢,因为读取永远都只需要一步,而查找却可能需要多
步。
char* array[] = { "apples", "bananas", "cucumbers", "dates", "elderberries" };
//查找dates
int sz = sizeof(array) / sizeof(array[0]);
for (int i = 0; i < sz; i++)
{
if (strcmp("dates", array[i])==0)
{
printf("找到了,其索引为:%d\n", i);
break;
}
}3.插入
往数组里插入一个新元素的速度,取决于你想把它插入到哪个位置上。
假设我们想要在购物清单的末尾插入 "figs" 。那么只需一步(回忆计算机访问内存的特点)。
char* array[6] = { "apples", "bananas", "cucumbers", "dates", "elderberries" };
//在末尾插入"figs"
array[5] = "figs";
但在数组开头或中间插入,就另当别论了。这种情况下,我们需要移动其他元素以腾出空间,
于是得花费额外的步数。
例如往索引 2处插入 "figs" ,如下所示。
第 1步: "elderberries" 右移。
第 2步: "date" 右移。
第 3步: "cucembers" 右移。
第 4步:至此,可以在索引 2处插入 "figs" 了。
如上所示,整个过程有 4步,开始 3步都是在移动数据,剩下 1步才是真正的插入数据。
最低效(花费最多步数)的插入是插入在数组开头。因为这时候需要把数组所有的元素都往右移。
于是,一个含有 N个元素的数组,其插入数据的最坏情况会花费 N + 1步。即插入在数组开头,导
致 N次移动,加上一次插入。
4.删除
数组的删除就是消掉其某个索引上的数据。
我们找回最开始的那个数组,删除索引 2上的值,即 "cucumbers" 。
第 1步:删除 "cucumbers" 。

虽然删除 "cucumbers" 好像一步就搞定了,但这带来了新的问题:
数组中间空出了一个格子。因为数组中间是不应该有空格的,所以,我们得把 "dates" 和 "elderberries" 往左移。
第 2步:将 "dates" 左移。
 第 3步:将 "elderberries" 左移。
第 3步:将 "elderberries" 左移。

结果,整个删除操作花了 3步。其中第 1步是真正的删除,剩下的 2步是移数据去填空格。
所以,删除本身只需要 1步,但接下来需要额外的步骤将数据左移以填补删除所带来的空隙。跟插
入一样,删除的最坏情况就是删掉数组的第一个元素。因为数组不允许空元素,当索引0空出,那
么剩下的所有元素都要往左移去填空。
可以推出,对于含有 N个元素的数组,删除操作最多需要 N步。
既然学会了如何分析数据结构的时间复杂度,那就可以开始探索各种数据结构的性能差异了。了解
这些非常重要,因为数据结构的性能差异会直接造成程序的性能差异。
总结
理解数据结构的性能,关键在于分析操作所需的步数。采取哪种数据结构将决定你的程序是
能够承受住压力,还是崩溃。
不同的数据结构有不同的时间复杂度,类似地,不同的算法(即使是用在同一种数据结构
上)也有不同的时间复杂度。既然我们已经学会了时间复杂度的分析方法,那么现在就可以用它来
对比各种算法,找出能够发挥代码极限性能的那个。
这正是下一章所要讲的。