拟合算法

文章目录

拟合算法
- - 概念
- 确定拟合曲线
- - 最小二乘法的几何解释
  - 求解最小二乘法
  - matlab求解最小二乘法
  - 如何评价拟合的好坏
  - 计算拟合优度的代码

概念

在前面的篇幅中提到可以使用插值算法，通过给定的样本点推算出一定的曲线从而推算出一些想要的值。但存在一些问题。一是若样本点过多，那么多项式的次数过高会造成龙格现象；二是为了避免龙格现象而通过分段的思想求得拟合曲线，但这样会导致曲线函数非常复杂。

针对以上问题，在拟合问题中，不需要曲线一定经过给定的点。拟合问题的目标是寻求一个函数（曲线），而该函数尽可能设置得较为简单，使得该曲线在某种准则下与所有的数据点最为接近，即只要保证误差足够小即可，（最小化损失函数），这就是拟合是思想。

确定拟合曲线

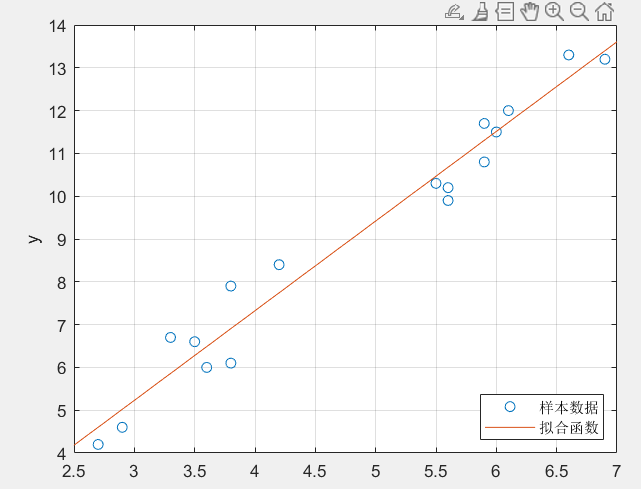
给定一组数据[x,y]，找出y和x之间的拟合曲线

在matlab上通过画图得出这组数据对应的图像

plot(x,y,'o');

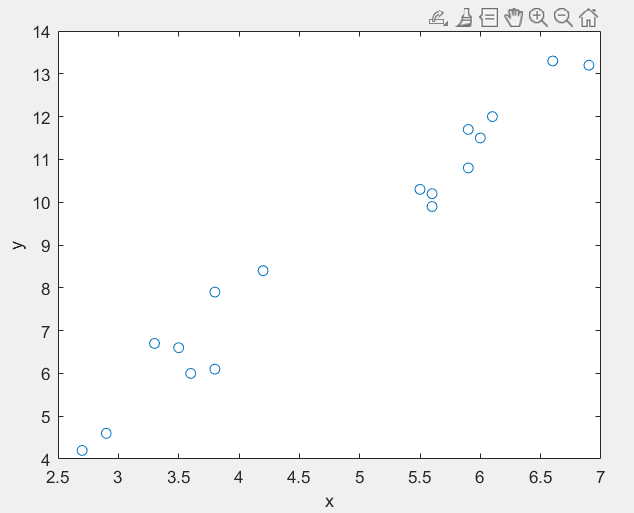
拟合一个曲线去接近样本点，这里我用一个简单的拟合曲线y=kx+b。现在的问题是，k和b取何值时，样本点和拟合曲线最接近。

最小二乘法的几何解释

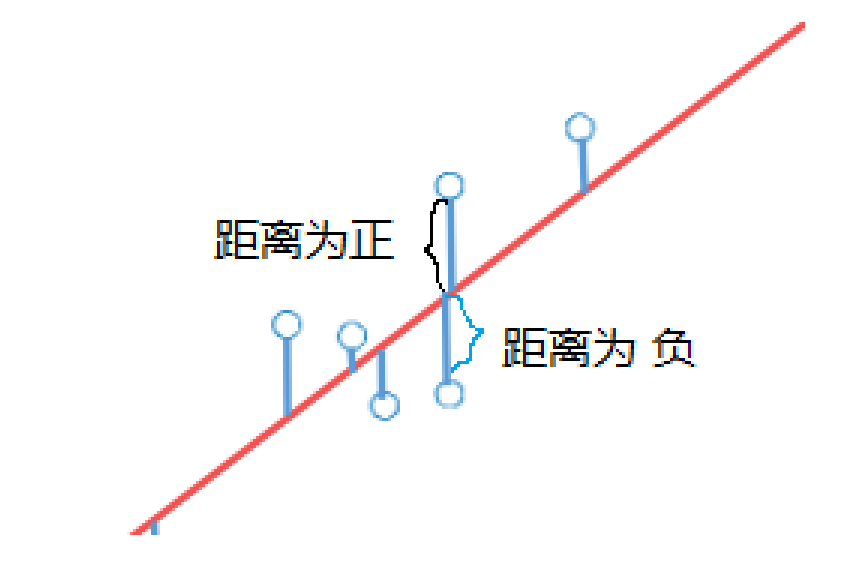
第一种定义有绝对值，后续不容易求导，因此计算较复杂。所以我们往往使用第二种定义，这正是最小二乘法的思想
我们也不使用三次方，因为三次方计算样本点到拟合曲线的距离会出现负数，那么该距离就会正负抵消
我们也不使用四次方，使用4次方时，若出现某个异常值离曲线较远，那么该拟合曲线受到的影响较大

求解最小二乘法

最终落脚到的两个公式：k^{^{</sup>和b<sup>}}推导公式

该公式通过对k和b一介求导，然后分离系数所得

matlab求解最小二乘法

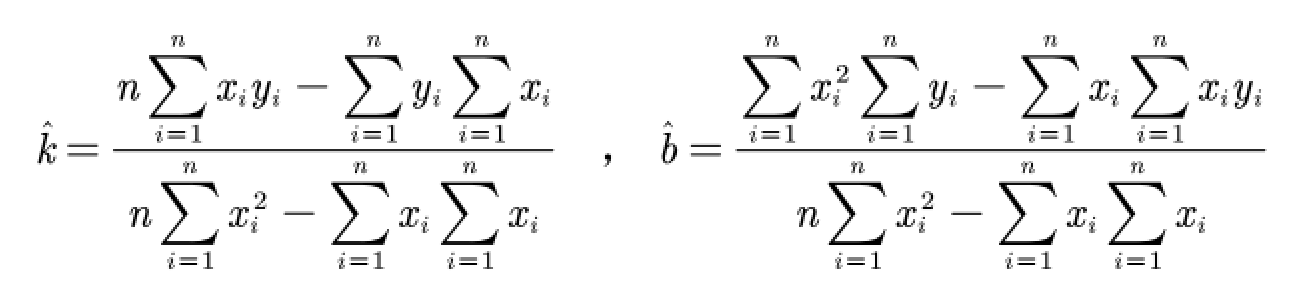
根据公式不难得出代码

plot(x,y,'o');
xlabel("x");
ylabel("y");
n=size(x,1);%% 数据的个数
k=(n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x));
b=(sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x));
hold on;%% 写上这句后续可以继续在之前的图形上画图形
grid on;%% 图形显示网格线
f=@(x) k*x+b; %% f=kx+b是匿名函数，该函数图形不需要另外传参数也能形成图形
fplot(f,[2.5,7]);
legend('样本数据','拟合函数','location','southeast');

f函数是匿名函数，该函数图形不需要另外传参数也能形成图形。在matlab中画出图形需要传参。比如正常情况下f函数需要传参x否则不能画出图形，而匿名函数系统会根据需求自己给出一定范围的参数以得画出图形

匿名函数的基本用法

handle = @(arglist) anonymous_function

其中handle为调用匿名函数时使用的名字。
arglist为匿名函数的输入参数，可以是一个，也可以是多个，用逗号分隔。
anonymous_function为匿名函数的表达式。
注意输入参数和表达式之间要用空格

fplot可用于画出匿名一元函数的图形

基本用法

fplot(f,xinterval)

将匿名函数f在指定区间xinterval绘图。xinterval = [xmin xmax] 表示定义域的范围

如何评价拟合的好坏

根据SST、SSE、SSR可以证明：

SST=SSE+SSR
拟合优度：0<=1-SSE/SST<=1;而SSE误差平方和越小，拟合优度R²越接近1。误差越小说明拟合的越好
注意：拟合优度R²只能用于拟合函数是线性函数，若拟合函数是其他函数，直接看误差平方和即可，SSE越小，说明拟合度越好
线性函数是指在函数中，参数仅以一次方出现，且不能乘以或除以其他任何的参数，并不能出现参数的复合函数形式。该参数不是指自变量x。比如y=kx+b，该参数指的是区别于自变量x和因变量y以外的参数k和b。

计算拟合优度的代码

plot(x,y,'o');
xlabel("x");
ylabel("y");
n=size(x,1);%% 数据的个数
k=(n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x));
b=(sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x));
hold on;%% 写上这句后续可以继续在之前的图形上画图形
grid on;%% 图形显示网格线
f=@(x) k*x+b; %% f=kx+b是匿名函数，该函数图形不需要另外传参数也能形成图形
fplot(f,[2.5,7]);
legend('样本数据','拟合函数','location','southeast');
y_hat=k*x+b;
SSR=sum((y_hat-mean(y)).^2); % 回归平方和
SSE=sum((y-y_hat).^2); % 误差平方和
SST=sum((y-mean(y)).^2); % 总体平方和
disp(SST-SSE-SSR);
R_2=SSR/SST; % 拟合优度
disp(R_2);

SST-SSE-SSR的结果不为0的原因是在matlab中浮点数做运算一定程度上结果不精准，但结果是5.6843^{^-14}结果是非常小的即非常接近0
[外链图片转存中…(img-WkmLP3WM-1692188156893)]
SST-SSE-SSR的结果不为0的原因是在matlab中浮点数做运算一定程度上结果不精准，但结果是5.6843^{^-14}结果是非常小的即非常接近0
拟合度为0.9635非常接近1了，说明该拟合函数的拟合度较好