一、层次分析法简介

层次分析法（Analytic Hierarchy Process，AHP）是一种用于多准则决策分析和评估问题的定量方法，常用于数学建模中。它是由数学家托马斯·赛蒂（Thomas Saaty）开发的。

层次分析法将复杂的决策问题分解成多个层次，从目标层到准则层和备选方案层。具体步骤如下：

1. 确定决策目标：明确决策问题的目标，例如选择最佳方案或评估不同选项之间的优先级。

2. 构建层次结构：将决策问题分解成多个层次，包括目标层、准则层和备选方案层。目标层是最高层，准则层是中间层，包含影响决策的关键准则，备选方案层是最底层，包含可供选择的具体方案。

3. 建立比较矩阵：对于每个层次的准则和方案，构建一个比较矩阵，用于评估它们之间的相对重要性或优先级。在比较矩阵中，根据一定的标度（通常是1到9的范围），比较两个元素之间的重要性，填写对应的数值。

4. 计算权重向量：通过对比较矩阵进行一系列数学运算，计算出每个层次的准则和方案的权重向量。具体的计算方法包括计算特征向量、一致性指标和一致性比率。

5. 一致性检验：通过计算一致性指标和一致性比率，检验所建立的比较矩阵的一致性。一致性检验可以评估比较矩阵是否合理和可靠。

6. 综合评估与决策：基于权重向量和一致性检验的结果，对备选方案进行综合评估，确定最佳方案或进行优先排序。

层次分析法可以帮助决策者在复杂的多准则决策问题中进行定量分析和评估，提供科学的决策依据。它在许多领域中都有广泛的应用，例如工程管理、项目选择、资源分配、商业决策等。

二、实例

例一

例题：假设你是一家电子公司的产品经理，公司计划推出一款新的智能手机。你需要对不同的功能进行评估，以确定哪些功能是最重要的。请使用层次分析法对以下四个功能进行评估：摄像头质量、处理器性能、电池续航时间和屏幕分辨率。

解答：
1. 创建一个层次结构，将四个功能作为最高层次的标准。
2. 创建一个判断矩阵，将每个功能与其他功能进行比较，根据其相对重要性给出权重。
3. 计算每个功能的权重。
4. 检查一致性，确保判断矩阵的一致性。
5. 根据每个功能的权重，确定最重要的功能。

具体步骤如下：
1. 创建层次结构：
   - 最高层次：功能
   - 第二层次：摄像头质量、处理器性能、电池续航时间、屏幕分辨率

2. 创建判断矩阵：
   - 摄像头质量：1, 3, 5, 7
   - 处理器性能：1/3, 1, 3, 5
   - 电池续航时间：1/5, 1/3, 1, 3
   - 屏幕分辨率：1/7, 1/5, 1/3, 1

3. 计算权重：
   - 根据判断矩阵的列平均值计算每个功能的权重：
     - 摄像头质量：(1+3+5+7)/4 = 4
     - 处理器性能：(1/3+1+3+5)/4 = 2.25
     - 电池续航时间：(1/5+1/3+1+3)/4 = 1.08
     - 屏幕分辨率：(1/7+1/5+1/3+1)/4 = 0.47

4. 检查一致性：
   - 计算一致性指标 CI：(最大特征值 - 层次结构层数) / (层次结构层数 - 1) = (4 - 4) / (4 - 1) = 0
   - 计算一致性比例 CR：CI / RI，RI为随机一致性指标，根据层次结构层数查表得到RI=0.9
   - CR = 0 / 0.9 = 0，CR小于0.1，判断矩阵一致性通过。

5. 确定最重要的功能：
   - 摄像头质量：4
   - 处理器性能：2.25
   - 电池续航时间：1.08
   - 屏幕分辨率：0.47

根据计算结果，摄像头质量是最重要的功能，其次是处理器性能、电池续航时间和屏幕分辨率。因此，在开发智能手机时，应优先考虑提高摄像头质量。

例二

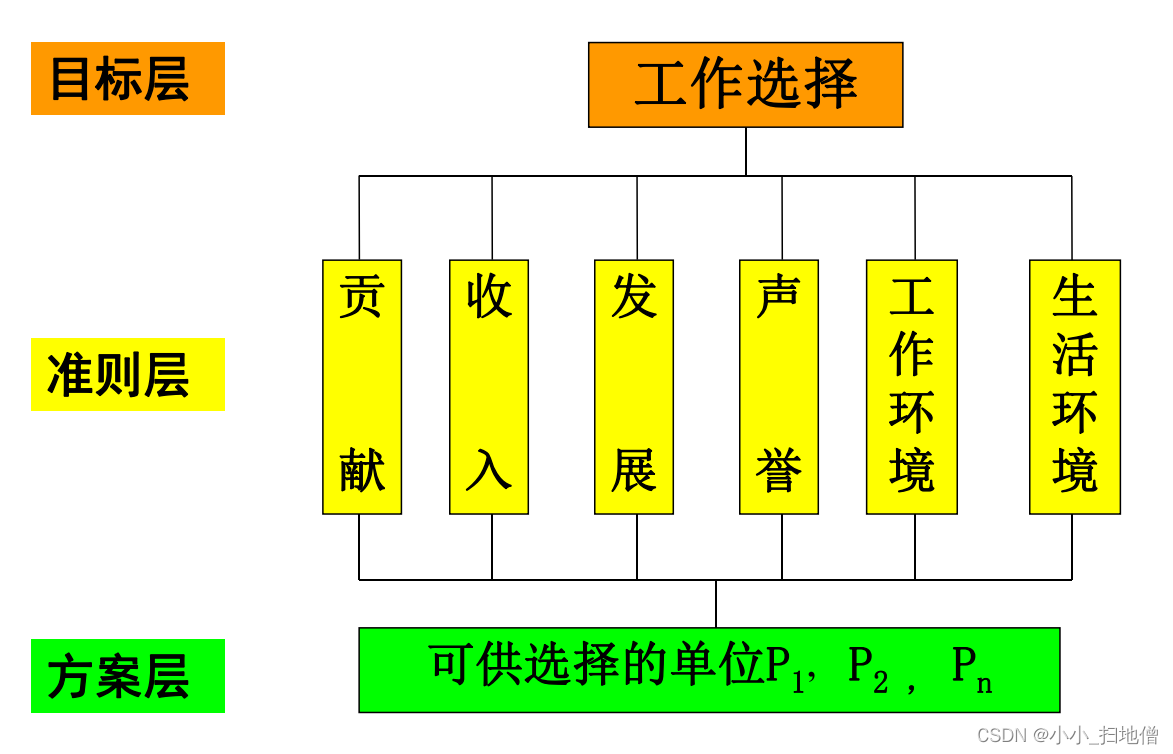
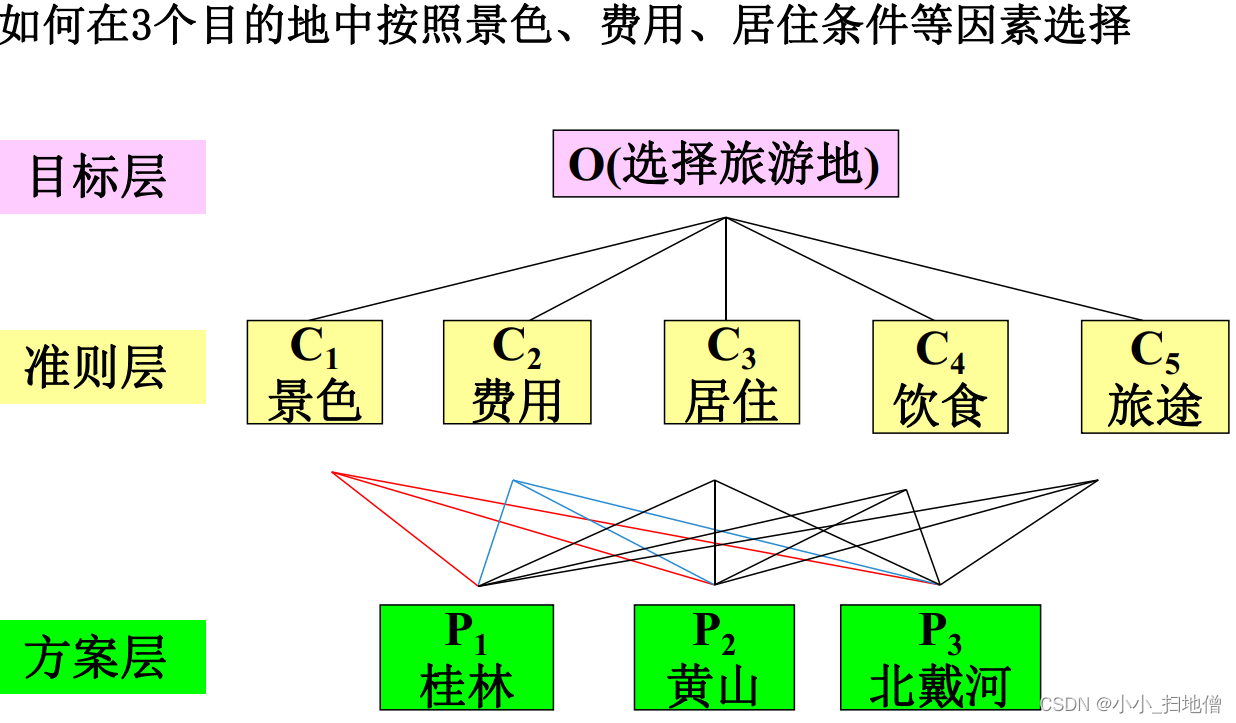
例三、选择旅游地

三、MATLAB代码

使用方法
（1）构造判断矩阵A
（2）将下文代码复制粘贴到Matlab中即可
例如：A=[1 3 5;0.33 1 3;0.2 0.33,1]

disp('请输入准则层判断矩阵A(n阶)');
A=input('A=');
[n,n]=size(A);
[V,D]=eig(A);%求得特征向量和特征值
%求出最大特征值和它所对应的特征向量
tempNum=D(1,1);%特征值的初值
pos=1;
for h=1:n
if D(h,h)>tempNum
tempNum=D(h,h);
pos=h;%标记的第一个数
end
end

%找最大特征值及其对应的位置
w=abs(V(:,pos));%找出最大特征值对应的特征向量
w=w/sum(w);%归一化处理
t=D(pos,pos);
disp('准则层特征向量w=');disp(w);disp('准则层最大特征根t=');disp(t);
%以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59 1.60 1.61 1.615 1.62 1.63];
CR=CI/RI(n);
if CR<0.10
disp('此矩阵的一致性可以接受!');
disp('CI=');disp(CI);
disp('CR=');disp(CR);
else disp('此矩阵的一致性验证失败，请重新进行评分!');
end